9. Оценка внутренней стоимости облигаций

Оценка внутренней стоимости облигаций зависит от способа выплаты дохода.

Рассмотрим самый простой случай – облигация с нулевым купоном (процент по облигации не выплачивается). Поскольку денежные поступления по годам, за исключением последнего года, равны нулю, внутренняя стоимость облигации определяется следующим образом:

где V он — стоимость облигации с нулевым купоном с позиции инвестора (теоретическая стоимость);

N — сумма, выплачиваемая при погашении облигации (номинал);

r – ставка дисконтирования;

n — число лет, через которое произойдет погашение облигации.

Бессрочная облигация предусматривает неопределенно долгую выплату дохода ( D ) в установленном размере. В этом случае ожидаемые выплаты представляют собой бессрочный аннуитет, поэтому

Vоб = D / r

где V об – стоимость бессрочной облигации;

r – ставка дисконтирования;

D – купонный доход.

Безотзывная облигация с постоянным доходом порождает поток купонных выплат, а также предусматривает погашение облигации по номинальной цене в установленный срок. В связи с этим, формула для оценки ее внутренней стоимости состоит из двух слагаемых:

где V опд – стоимость безотзывной облигации с постоянным доходом;

D – ежегодный купонный доход;

r – ставка дисконтирования;

N — сумма, выплачиваемая при погашении облигации (номинал);

t – номер года;

n – число лет, оставшихся до погашения облигации.

Отзывная облигация может быть погашена досрочно и при этом выкупная цена может не совпадать с номиналом. Оценка таких облигаций осуществляется также с использованием этой формулы в которой нарицательная стоимость N заменена выкупной ценой.

В заключение необходимо особо обратить внимание на то, что в рассмотренных формулах подразумевается капитализация получаемых доходов (процентов, дивидендов) с доходностью, равной ставке дисконтирования. Например, в случае с облигацией ее оценка, полученная с помощью формулы (2.2.13), будет верна, если регулярно получаемые проценты не используются для потребления, а немедленно инвестируются в те же облигации или в ценные бумаги с той же доходностью и степенью риска. В случае если возможность такого инвестирования отсутствует или не планируется, применение формулы (2.2.13) является ошибкой.

10. Доход и доходность. Доходность акций и облигаций.

Доход – абсолютный показатель выраженный в конкретных единицах например рублях, доходность – относительный выражается в %. В зависимости от вида финансового актива в качестве дохода о чаще всего выступают дивиденд, процент, прирост капитализированной стоимости, когда необходимо принять решение о целесообразности приобретения финансовых активов. Доходность актива ( d ) – это показатель, рассчитываемый соотнесением дохода ( D ), генерируемого данным финансовым активом, и величины инвестиции (I) в этот актив: d = D / I Доходность, исчисленная в процентах, по существу представляет собой рентабельность данного актива или норму прибыли, однако традиционно термин «рентабельность» используется по отношению к материальным активам, а термин «доходность» по отношению к финансовым активам и капиталу. В финансовых расчетах доход, обеспечиваемый каким-либо активом, обычно разделяют на две составляющих: 1) регулярные выплаты владельцу актива, 2) рост стоимости самого актива. Соответственно ожидаемая доходность также будет складываться из двух составляющих – текущей и капитализированной доходности. Выбирая для покупки финансовый актив, инвестор должен расставить для себя приоритеты — что важнее, регулярный доход или прирост стоимости актива.

Доходность облигации.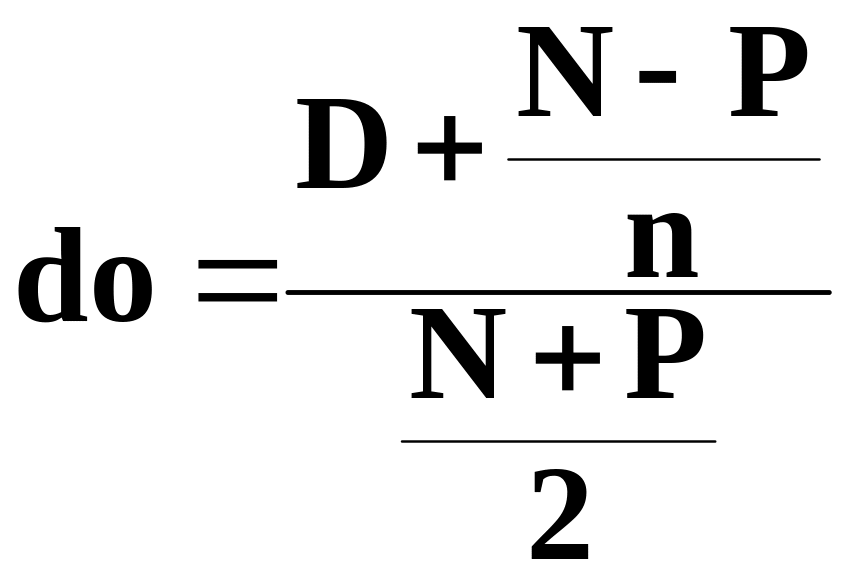

где do — доходность облигации;

N — номинал облигации;

Р — текущая цена (на момент оценки);

D — купонный доход;

n — число лет, оставшихся до погашения облигации.

Достоинством показателя do , как и любого другого показателя эффективности, является возможность использования его в сравнительном анализе при выборе вариантов инвестирования в те или иные облигации.

Еще одной характеристикой доходности облигации является показатель купонной доходности, рассчитываемый по следующей формуле

Чаще всего этот показатель не рассчитывается, а задается в виде купонной ставки. Значимость этого показателя для оценки доходности облигации невысока, а именно: эта ставка дает оценку доходности облигации лишь в момент ее эмиссии; в дальнейшем она используется в основном для расчета купонного дохода.

Облигации с правом досрочного погашения имеют, кроме рассмотренных, еще одну характеристику — доходность досрочного погашения ( Yield to Call , YTC). Этот показатель дает оценку доходности на момент отзыва облигации с рынка, или ее досрочного погашения

Д оходность акции.

-дивиденд за 1 год(текущий доход)

- ожидаемая цена акции на момент ее предполагаемой продажи

- рыночная цена акции на момент принятия решения о покупке

Доходность акции с равномерно возрастающими дивидендами

где da – доходность акции;

dat – текущая (дивидендная) доходность акции;

dac – капитализированная доходность акции;

D₀– последний полученный к моменту оценки дивиденд по акции;

D₁– ожидаемый дивиденд;

P₀– цена акции на момент оценки;

g– темп прироста дивиденда.

Из формулы видно, что ожидаемая капитализированная доходность обыкновенной акции с равномерно возрастающим дивидендом совпадает с темпом прироста дивиденда или с темпом прироста цены акции. Таким образом, показатель g имеет несколько интерпретаций: во-первых, это капитализированная доходность; во-вторых, темп прироста дивиденда; в-третьих, темп прироста цены акции.

Рассчитывать доходность акций имеет смысл только за какой-то определённый период, поэтому при расчёте доходности нужно определиться с периодом. В любом случае, для расчёта доходности акции нужно знать начальное и конечное значение (цену) за выбранный период. Доход от акции образуется за счёт разницы цен покупки и продажи. В процентном соотношении к цене покупки этот доход называется доходностью акций.Кроме дохода от разницы цен покупки и продажи акции инвестор также может получить дополнительный доход, называемый дивидендным (от выплат по дивидендам).