Тема 10 Классификация статистических методов. Базовые методы анализа маркетиноговой информации

1. Классификация статистических методов.

2. Ряды распределения маркетинговой информации: атрибутивный и вариационный ряд

3. Обобщающие показатели: интерпретация типических значений.

4. Показатели вариации.

5. Понятие статистической гипотезы.

6. Построение таблиц сопряженности признаков.

1. Классификация статистических методов

Статистические методы делятся на одно- и многомерные. Одномерные методы (univariate techniques) используются тогда, когда все элементы выборки оцениваются единым измерите­лем, либо если этих измерителей несколько для каждого элемента, но каждая переменная ана­лизируется при этом отдельно ото всех остальных.

Одномерные методы (univariate techniques)

Методы статистического анализа, применяемые для анализа данных в случаях, если сущест­вует единый измеритель для оценки каждого элемента выборки, либо если этих измерителей несколько, но каждая переменная анализируется отдельно ото всех остальных.

Многомерные методы (multivariate techniques) прекрасно подходят для анализа данных, если для оценки каждого элемента выборки используется два или больше измерителей, а эти пере­менные анализируются одновременно. Такие методы применяются для определения одновре­менных взаимосвязей между двумя или больше явлениями.

Многомерные методы (multivariate techniques)

Методы статистического анализа, применяемые для анализа данных, если для оценки каж­дого элемента выборки используется два или больше измерителя и эти переменные анали­зируются одновременно. Данные методы применяются и определения одновременных взаимосвязей между двумя или больше явлениями.

Многомерные методы отличаются от одномерных прежде всего тем, что при их использова­нии центр внимания смещается с уровней (средних показателей) и распределений (дисперсий) явлений и сосредотачивается на степени взаимосвязи (корреляции или ковариации) между этими явлениями [15]. Оба этих вида статистических методов анализа подробно описаны в по­следующих главах, но сейчас мы покажем, как разные методы взаимосвязаны в общей схеме классификации.

Одномерные методы можно классифицировать на основе того, какие данные анализируют­ся: метрические или неметрические. Метрические данные (metric data) измеряются по интер­вальной шкале или относительной шкале

Метрические данные (metric data)

Данные, которые по своей природе интервальные или относительные.

Неметрические данные (nonmetric data) оцениваются по номинальной или порядковой шкале.

Неметрические данные (nonmetric data)

Данные, полученные на основе измерений по номинальной или порядковой шкале.

Затем эти методы делят на классы на основе того, сколько выборок — одна, две или более — анализируется в ходе исследований. Заметим, что число выборок определяется тем, как ведется работа с данными для конкретного анализа, а не тем, каким способом собирались данные. На­пример, данные по лицам мужского и женского пола можно получить в пределах одной выбор­ки, но если их анализ нацелен на выявление разницы в восприятии, основанной на разнице полов, исследователю придется воспользоваться двумя разными методами выборки. Выборки считаются независимыми, если они выделены из разных генеральных совокупностей произ­вольно. Для анализа данные, относящиеся к разным группам респондентов, например собран­ные от лиц женского и мужского пола, обычно обрабатываются как независимые выборки.

С другой стороны, если данные по двум выборкам относятся к одной и той же группе респон­дентов, выборки считаются объединенными в пары.

Что касается метрических данных, то если существует только одна выборка, может использо­ваться z- и г-критерий. Если же независимых выборок две или больше, в первом случае можно воспользоваться z- и /-критерием для двух выборок, в во втором — методом однофакторногодис­персионного анализа. Для двух связанных выборок используется парный /-критерий. Если речь идет о неметрических данных по одной выборке, исследователь может воспользоваться критерия­ми частотного распределения, хи-квадратом, критерием Колмогорова—Смирнова (K—S), крите­рием серий и биномиальным критерием. Для двух независимых выборок с неметрическими данными можно прибегнуть к следующим методам анализа: хи-квадрат, Манна—Уитии, ме­дианы, К—С, однофакторным дисперсионным анализом Крускала—Уоллиса (ДА К-У). В от­личие от этого, если существует две или больше взаимосвязанных выборок, следует воспользо­ваться критериями знаков, Мак-Нсмарии Уилкоксона (рис. 14.6).

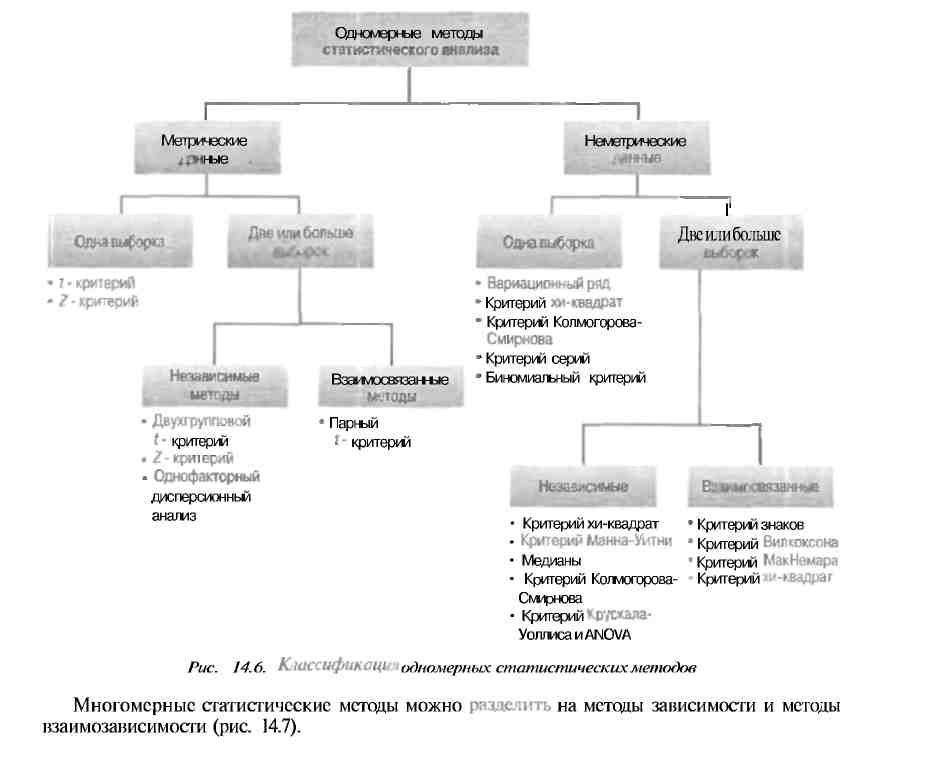
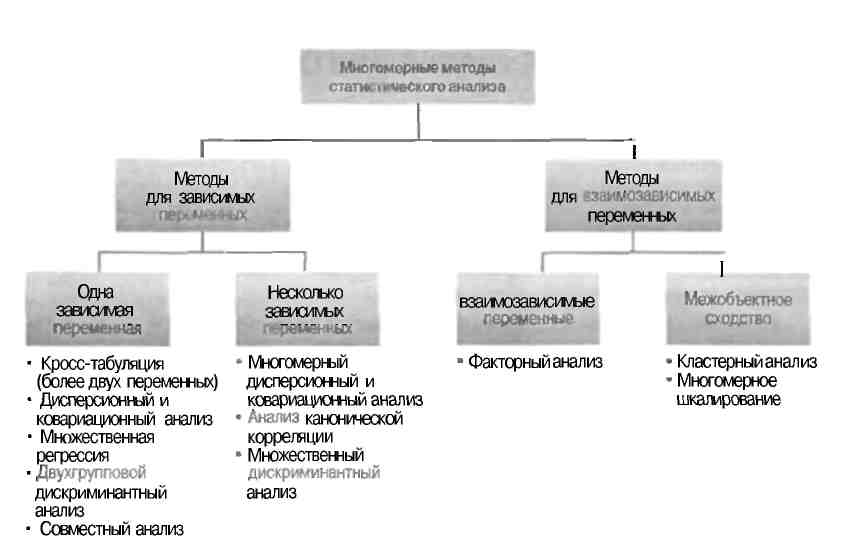
Рис. 14.7. Классификация многомерных статистических методов

Методы зависимости (dependence techniques) применяются в случаях, когда одна или боль­ше переменных идентифицированы как зависимые, а остальные — как независимые.

Методы зависимости (dependence techniques)

Методы, применяемые в случаях, когда одна или больше переменных идентифицированы как зависимые, а остальные - как независимые.

Если есть только одна зависимая переменная, используются такие методы анализа, как кросс-табуляция, дисперсионный и ковариационный анализ, регрессионный анализ, двух­групповой дискриминантный анализ и совместный анализ. Однако, если имеется больше од­ной зависимой переменной, следует воспользоваться многомерными методами анализа: дис­персионным и ковариационным, методом канонической корреляции и множественным дис-криминантным анализом. При применении методов взаимозависимости (interdependent techniques) переменные не подразделяются на зависимые и независимые; напротив, исследует­ся весь набор взаимозависимых взаимосвязей.

Методы взаимозависимости (interdependent techniques)

Многомерные статистические методы, цель которых - сгруппировать данные по лежащему в основе сходству, что позволяет интерпретировать разные структуры данных. При этом пере­менные не подразделяются на зависимые и независимые.

Методы данного типа нацелены прежде всего на выявление взаимозависимости перемен­ных либо межобъектного сходства. При исследовании взаимозависимости переменных чаще всего применяется факторный анализ. Анализ межобъектного сходства можно вести, используя методы кластерного анализа и многомерного шкалирования [17].