Критерий Дарбу интегрируемости функций по Риману

Пусть и .

Для разбиения обозначим .

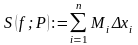верхняя сумма Дарбу.

нижняя сумма Дарбу.

Утверждение 1.10. .

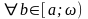
Теорема 1.2 (Дарбу). : .

Лемма 1.1.

, .

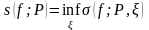◄ Требуется доказать:

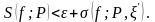
Пусть

►

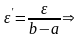
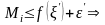
Теорема 1.3 (критерий Дарбу интегрируемости функции по Риману).

Пусть ограничена на .

◄ Достаточность:

при

В силу равенства пределов , при

Необходимость:

( при Аналогично можно показать, что ►

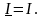Критерий интегрируемости функций по Риману

Теорема 1.4. Пусть ограничена на .

.

◄ Необходимость:

при

(Достаточность доказана выше). ►

Лекция №4 Свойства интеграла Римана

1) Линейность

Если

.

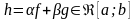
Замечание 1.4. Множество интегрируемых функций – линейное пространство.

Интеграл – линейный функционал: ,

◄ при .

Значит

Остается перейти к пределу при .►

2) Аддитивность Если

, и .

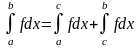◄ 1. Докажем, что сужение 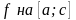интегрируемая функция

2. .

При получаем .

Если 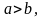определим:

.►

Следствие 1.2.

.

3) Общая оценка интеграла

.

◄

.►

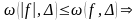
Следствие 1.3.

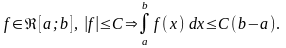
4) Монотонность интеграла

,

.

Доказательство следует из .

Следствие 1.4. ,

в частности, если

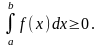
5) Теорема о среднем

Лемма.

1. Если ,

2. Если .

◄1) если

,

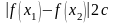2) ►

Теорема 1.5. , ,

, .

◄

.

Если , то = .►

Следствие 1.5. Если

.

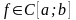
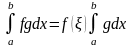◄Так как – теорема о промежуточном значении непрерывной функции. ►

В частност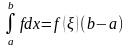и (при ).

Лекция №5 Интеграл как функция верхнего предела интегрирования

Рассмотрим .

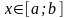Введём функцию По свойству интеграла: для

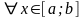
Теорема 1.6. .

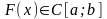◄ Пусть

где Получим: – это означает непрерывность (Малому приращению аргумента соответствует малое приращение функции.) ►

Теорема 1.7. Пусть и непрерывна в точке

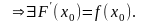
◄ Так как непрерывна в точке :

,

►

Формула Ньютона-Лейбница

Теорема 1.8. Пусть и имеет конечное число точек разрыва

,

где любая первообразная функции .

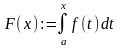◄ , , где – первообразная в силу теоремы 1.7 (за исключением точек разрыва .

,

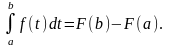
Если – любая первообразная функции .►

Пример 1.4.

Формула замены переменных и интегрирование по частям в определённом интеграле

Формула замены переменных

Теорема 1.9. Пусть 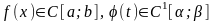(непрерывно дифференцируемая)

◄ Пусть , где , покажем, что – первообразная для По правилу дифференцирования сложной функции

►

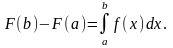Пример 1.5.

,

Замечание 1.5. , вообще говоря, может не быть непрерывной.

Формула интегрирования по частям

Теорема 1.10. Пусть .

◄ Введём

.►

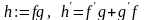
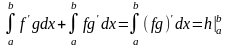Лекция №6 Геометрические приложения определённого интеграла

Аддитивная функция ориентированного промежутка

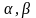Определение 1.12. Пусть каждой упорядоченной паре точек отрезка поставлено в соответствие число , причем так, что

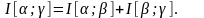(1.1)

Тогда называют аддитивной функцией ориентированного промежутка (АФОП).

1) : ;

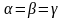2)

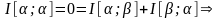
Пример 1.6.

– интеграл Римана есть АФОП.

По свойству интеграла .

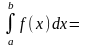
Утверждение 1.11.

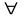
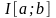(АФОП)

(1.2)

где функция точек отрезка

Полагая

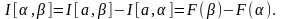
Утверждение 1.12.

порождает по формуле (1.2) АФОП .

Пример 1.7.

.

Теорема 1.11. Если на задана АФОП и

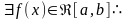
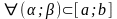
(1.3)

.

◄

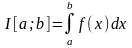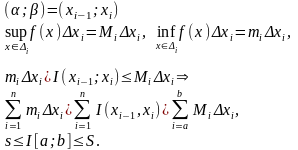
Далее переходим к пределу при .►