Лабораторна робота №4 атд граф для пошуку шляху Вступ

Для того, щоб давати корисні поради, система MapQuick потребує засобу пошуку найкоротшого шляху між двома точками. MapQuick необхідна абстракція для відображення інформації про вулиці, зв'язок між вулицями, а також можливі шляхи руху. Хоча наступна лабораторна робота буде спрямована на створенням структури даних для представлення самих вулиць, це завдання буде зосереджено на розвитку здатності знаходити найкоротший шлях між двома точками.

Для цього, MapQuick потребує абстракції графа для подання з'єднання, абстракції шляху для опису витрат на пересування певним курсом, і алгоритму пошуку шляху для пошуку найкоротших шляхів.

Хоча ми не вказуємо назви, сигнатури методів, або специфікації вашого абстракції графа, ми надаємо специфікацію шляху і надати вам формат файлу для драйвера тестування. Драйвер тестування буде виконувати сценарій команд та виводити результати на стандартний вивід.

Графи

MapQuick представляє зв’язані вулиці за допомогою орієнтованого графа. Ви буде здійснювати загальне уявлення граф, який може бути використаний для різних цілей, в тому числі MapQuick's.

Орієнтований граф складається з множини вершин деякі з яких можуть бути з'єднані ребрами. У орієнтованому графі, ребра мають напрям: вузол B може мати ребро у вузол C, але вузол C не обов'язково зв’язаний з вузлом B. У нашому випадку не може бути лише одне ребро з даного вузла до іншого вузла, але може бути ребро з А в В і ребро з В в А.

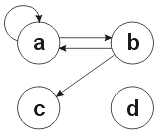
Рис. 1 Простий орієнтований граф з чотирма вершинами.

Дітьми вузла B є вузли, до яких є ребра з B. У наведеному вище прикладі дітьми B є А і С. Крім того, батьками B є вузли, з яких є ребра у В. У наведеному вище прикладі B має тільки одного батька, А.

Навантажені-вузли означає, що вузли в графах будуть мати деяку вартість пов’язану з ними, яка показує витрати на проходження даного вузла(вершини).

Концептуально, граф складається з вузлів(вершин) і ребер, що з'єднують вузли. (Проте на практиці часто подають графи інакше.) Якщо у вас є якісь запитання, що стосуються визначення графів, вам потрібно переглянути інші матеріали (наприклад, Wikipedia) перш ніж продовжувати далі.

Подання вулиць у вигляді вузлів

У поданні графу MapQuick, вулиці є вузлами (вершинами), а з'єднання між вулицями (перехрестя) представлені ребрами між ними в графі. Це має ряд переваг у порівнянні з альтернативним підходом (у якому вузли представляють перетини, а ребра представляють вулиці); Тут ми перерахуємо лише деякі з них:

• На перехресті може бути заборонений проїзд у певних напрямках. Це може бути представлено шляхом з’єднання (створення ребер між ними) тільки тих вулиць, які представляють допустимі моделі руху.

• Типове подання графу представляє вершини як (Java) об’єкти, проте подає ребра неявно, наприклад, шляхом зберігання для кожної вершини переліку інших вершин (до яких вона має ребро). У такому поданні, вершини можуть містити додаткову інформацію, але ребра ні. (Подання графів, що можуть зберігати інформацію у ребрах є дещо складнішим.) Тож підхід "вулиці є вершинами" дає зручне місце для зберігання довжини вулиці, яка буде мати важливе значення пізніше в проект MapQuick.

• Метою пошуку-маршруту є певна вулична адреса, а не перехрестя, і значно простіше шукати у графі певну вершину ніж ребро.

• Оскільки клієнти будуть розглядати і використовувати граф MapQuick як абстрактний об'єкт, то реалізувавши абстракцію, ваш код має бути в рівній мірі легко писати, читати, і відладжувати, незалежно від базової абстракції. Використання абстракції відмінної від "очевидної" допомагає перевірити свою абстракцію і може привести до кращого коду в довгостроковій перспективі.

АТД Graph