1.Классическая модель определения орз.

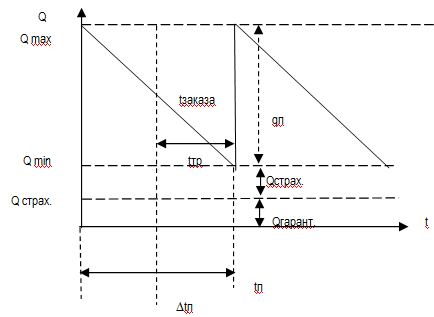
S(t) = Qmax – Q min – λt; S(t) = q – λt; q = λt; λ = q/t; t = q/λ

qп - объем поставки; tп – время поставки; tзаказа – точка заказа; ∆tп – время между поставками; tтр – время доставки товара; λ – интенсивность спроса

S(t) – функция спроса.

ОРЗ: Определение ср.РЗ.

Lобщ. + Lхр. = k + cq + h(q² / 2λ)

Lобщ. = k + cq; Lхр. = hT(q/2) = h(q/2)(q/2).

Lобщ./q = (k/q) + c + (hq/2λ) →min , (Lобщ./q)^| = (-k/q²) + 0 + (h/2λ)

(-k/q²) + (h/2λ) = 0; (k/q²) = (h/2λ); q² = (2λk)/h q = …..

Экономичным (оптимальным) размером заказа является величина партии материалов, которая позволит сократить до минимума ежегодную общую сумму расходов на выполнение заказа и хранение материалов. Методика определения экономичного размера заказа заключается в сравнении преимуществ и недостатков приобретения материалов большими и малыми партиями и в выборе размера заказа, соответствующего минимальной величине общих расходов на пополнение запасов. Соотношение размера заказа и расходов на поставку (выполнение заказов) и хранение материалов графически изображено на рис. 2.1.4.

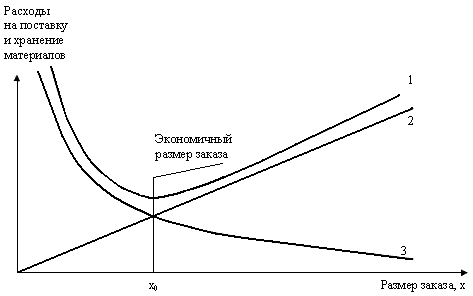
Рис. 2.1.4. Зависимость расходов на выполнение заказа

и хранение материалов от размера заказа Пусть х – число единиц, закупаемых в результате одного заказа. По мере того, как возрастает число закупаемых единиц материала, текущие расходы на хранение материалов (содержание запасов) увеличиваются (кривая 2). Одновременно с этим, при увеличении размера партии, количество заказов в год снижается. Это приводит к уменьшению расходов, связанных с выполнением заказов (кривая 3). Как видно из рис. 2.1.4, кривая общих годовых расходов (кривая 1) имеет минимум при х = х0. На основе количественной оценки зависимостей расходов на закупку и хранение материалов от количества закупаемого материала можно определить размер заказа, минимизирующий величину общих расходов при следующих допущениях: общее число единиц материала, составляющих годовые запасы, известно. величина спроса неизменна. выполнение заказов происходит немедленно, т.е. заказы выполняют в установленные сроки, время опережения известно и постоянно. расходы на оформление не зависят от их размера. цена на материал не изменяется в течение рассматриваемого периода времени. В соответствии с принятыми допущениями расходы на выполнение заказа и содержание запасов могут быть выражены формулой (2.1.1) где С1 и С21 – соответственно постоянные и переменные расходы, связанные с выполнением заказа и содержанием материалов; n – количество заказов в год; q/2 – средний размер запаса. Экономичный размер заказа определяется по формуле (2.1.2)

где Q – годовая потребность в материале. Приведенная формула устанавливает экономичный размер заказа для условий равномерного и строго определенного (детерминированного) потребления запасов. В практике работы предприятия могут иметь место: затянувшаяся поставка; в этом случае материал доставляется не разово, а в течение того или иного времени с определенной интенсивностью и потребляется производством равномерно; его использование начинается сразу же после начала поставок до того, как вся поставка фактически завершится; ускоренное использование; в этом случае интенсивность потребления запасов такова, что возможен дефицит материала. С учетом отмеченных специальных условий строят частные модели по определению экономичного размера заказа. Классическая модель наиболее экономичного размера партии представляет собой простейшую модель определения оптимального размера заказа. Основные предположения: спрос непрерывный и детерминированный, интенсивность поступления требований равна λ; время поставки τ постоянно и не зависит от размера заказа, весь заказ поступает в виде одной партии; оптимальная стратегия функционирования определяется из условия минимума средних годовых издержек. Исходя из этих предположений, размер заказа всегда будет одинаков, а уровень наличного запаса в момент поступления пополнения всегда один и тот же. Поскольку спрос неслучаен, а время поставки постоянно, в системе при поступлении требований отсутствует дефицит].Средние годовые издержки (TCU), зависящие от стратегии функционирования, включают фиксированные издержки, связанные с подачей заказа (K) и издержки содержания запаса (h), кроме того, учитывается закупочная стоимость товара (C).

3.Модель определения ОРЗ при планировании дефицита. В классической модели экономичного размера заказа дефицит продукции, необходимой для производства, не предусмотрен. Однако в случаях, когда потери из-за дефицита сравнимы с расходами на содержание излишних запасов, дефицит допустим. При наличии его модель экономичного размера заказа требует учета определенных методических особенностей. Наиболее общий случай движения текущего запаса при допущении дефицита материала представлен на рис. 2.1.6, где q – размер запаса в начале каждого интервала между поставками t (максимальный запас при дефиците). Весь интервал t делится на два периода:

время, в течение которого запас на складе имеется в наличии, t1; время, в течение которого запас отсутствует, t2.

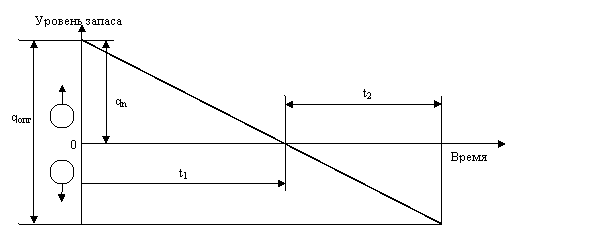
Рис. 2.1.6. Цикл движения текущих запасов при допущении дефицита Начальный размер запаса qn в этих условиях принят несколько меньше, чем оптимальный размер партии qопт. Задача управления запасом сводится к количественному определению размера снижения и установлению рациональной величины начального запаса. Критерием оптимальности партии поставки является минимальная сумма транспортно-заготовительных расходов, расходов на содержание запаса и потери из-за дефицита. Экономичный размер заказа определяется по формуле

где C3 – годовые потери из-за дефицита продукции. При значительном увеличении C3 отношение C3/(C2+C3) приближается к единице и оптимальный размер партий стремится к значению, которое было бы при отсутствии дефицита запасов. Если потери из-за дефицита незначительны, то отношение C3/(C2+C3) стремится к нулю, а оптимальный размер партии – к бесконечности, т.е. допускается большой дефицит запаса.

2.Модель определения ОРЗ при периодическом поступлении и равномерном расходе.Модель расчета оптимального размера заказа с постепенным пополнением используется в случае,когда допущение об одновременном оприхо-довании на склад поступившей партии поставки (мгновенной поставки) не может быть принято. Это относится к ситуациям с большими объемами поставок (например, при поставках по железной дороге) или при длительных процедурах приемки (например, при проверке по качеству). Для ситуации с так называемой продолженной поставкой необходимо учесть соотношение темпов прихода и отгрузки в рамках единичного учетного или планового периода. В общем случае объем поставки товарно-материальных ценностей превышает темп потребления. В противном случае запас не накапливается и предприятие работает на принципах поставки точно в срок или в состоянии дефицита. При продолженной поставке оптимальный размер заказа должен быть увеличен по сравнению с расчетом по Формула 8.1 и Формула 8.2 на стр. 251 и стр. 253, чтобы приходуемая в течение некоторого периода времени партия могла поддержать непрерывное потребление. Для работы в условиях продолженной поставки можно использовать следующую формулу:

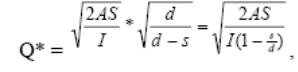
где Q^* – оптимальный размер заказа, единиц;

А – затраты на выполнение одного заказа, руб.

S – объем потребности в запасе, единиц;

I – затраты на содержание единицы запаса, руб.;

s – среднесуточная объем потребности в запасе, единиц/день;

d – среднесуточный объем поступления товарно-материальных ценностей на склад, единиц/день.Также можно использовать Формула 8.4 и при оценке поступлений и отгрузок в целом за плановый период:

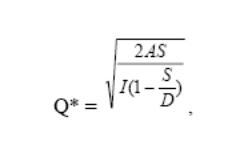
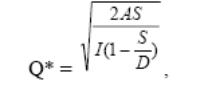
где Q^* – оптимальный размер заказа, единиц;

А – затраты на выполнение одного заказа, руб.

S – объем потребности в запасе, единиц;

I – затраты на содержание единицы запаса, руб.;

D – объем поступления товарно-материальных ценностей на склад в течение планового периода, единиц.