7.5. Оптимизация технологических процессов

Множество допустимых вариантов ТП является очень большим (сотни и тысячи возможных вариантов), поэтому задача оптимизации ТП является весьма трудоемкой и сложной. Технолог физически не может спроектировать такое количество вариантов, поэтому разработка технологических процессов носит субъективный характер и их качество зависит от его опыта и квалификации. Так как от качества ТП во многом зависит прибыль предприятия, то задача разработки оптимальных процессов является весьма актуальной.

Система проектирования ТП имеет многоуровневый характер, поэтому различают три уровня оптимизации:

• уровень маршрута;

• уровень операции;

• уровень перехода.

Оптимизация ТП выполняется по уровням: оптимизация операций осуществляется на основе использования оптимизированных переходов, а оптимизация процесса в целом (уровень маршрута) выполняется на основе оптимизированных операций. При такой иерархической оптимизации оптимизация на заданном уровне имеет глобальный характер по отношению к более низкому уровню и локальный характер по отношению к более высокому уровню.

Будем различать два вида оптимизации:

• структурная оптимизация;

• параметрическая оптимизация.

Оптимизация на уровне маршрута и операции является структурной, так как связана в основном с выбором структуры процесса или операции, в тоже время оптимизация на уровне перехода является параметрической, так как достигается путем варьирования параметрами перехода. Например, оптимальные режимы резания достигаются путем варьирования подачей, скоростью резания и припусками. Встречается также комбинированная структурно-параметрическая оптимизация.

Принципиальное отличие структурной оптимизации от параметрической оптимизации состоит в сущности оптимизируемых параметров. При структурной оптимизации они по своей природе являются неупорядоченными переменными. В параметрической оптимизации параметры представляют собой переменные, для которых существует понятие больше или меньше и которые естественным образом могут быть размещены в координатной системе. В структурной же оптимизации эти параметры не являются по существу числовыми. Параметрами структурной оптимизации являются, например, модели станков, типы инструментов, схемы базирования, т.е. варианты типовых решений.

М ножество допустимых вариантов может быть задано не аналитически, а алгоритмически, т.е. в виде правил, имеющих как формальный так и не формальный характер, поэтому возникают сложности с применением различных методов оптимизации. При структурной оптимизации наиболее общими методами оптимизации являются поисковые, при параметрической - методы линейного и нелинейного программирования.

Поисковые методы оптимизации используются, так как не накладывают особых ограничений на критерий оптимизации и область существования решений. Суть поисковых методов оптимизации заключается в нахождении последовательности вариантов технологических процессов (последовательном переборе возможных вариантов):

Т₁,…,Т_i,…,Т_n,

где каждый последующий вариант предпочтительнее предыдущего. В пределе указанная последовательность должна сходится к достаточно малой окрестности решения, т.е. варианту близкому к оптимальному. Наиболее часто применяют следующие поисковые методы оптимизации:

• метод случайного поиска;

• метод регулярного поиска;

• метод направленного поиска.

Р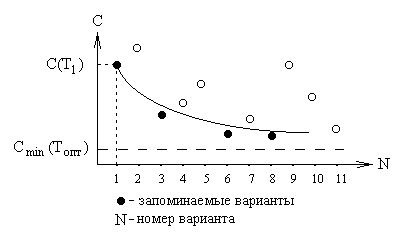 ис. 53. Выбор оптимального ТП методом случайного поиска

Как видно из рис. 53 выбор оптимального варианта ТП методом случайного поиска предполагает проектирование случайной последовательности вариантов технологического процесса с отбором вариантов, имеющих минимальную себестоимость по сравнению с предшествующими. Если провести усредненную кривую через точки для отобранных вариантов, то кривая себестоимости постепенно приближается к оптимальному в заданных условиях значению себестоимости процесса.

Сложность применения алгоритмов случайного поиска заключается в большой вариантности ТП, что в сочетании со сложностью алгоритмов проектирования (большими затратами машинного времени даже для современных компьютеров) не дает возможность просчитать большое количество вариантов и, следовательно, окончательный вариант будет далеко не оптимальным. Неформальный во многих случаях характер принятия, особенно при проектировании структуры процесса, не позволяет автоматически проектировать каждый вариант технологического процесса, поэтому требуется вмешательство технолога для оперативного принятия решений.

В настоящее время используются следующие направления сокращения вариантности проектируемых процессов:

• типизация технологических решений;

• изменение стратегии поиска;

• усиление режима диалога.

Типизация технологических решений применительно к условиям предприятия позволяет резко сократить количество генерируемых вариантов за счет использования лишь вариантов наиболее вероятных и прогрессивных для данного предприятия. Чем выше типизация решений, тем легче генерацию решений заменять на выбор решений и, следовательно, повышать быстродействие системы проектирования.

Структурная оптимизация рассматривает последовательно каждую задачу технологического проектирования. Таким образом, весь процесс проектирования расчленяется на несколько взаимосвязанных уровней. Процесс проектирования на каждом уровне представляет собой многовариантную процедуру. В результате проектирования на всех уровнях образуется граф допустимых вариантов ТП, отвечающих заданным ограничениям. Задача структурной оптимизации состоит в поиске ветви графа, обеспечивающей экстремум целевой функции.

П ри использовании метода случайного поиска обычно применяется стратегия поиска, которую можно назвать «сначала вглубь, а затем вширь». Для этой стратегии характерно то, что каждый вариант рассчитывается до конца (движение вглубь) независимо от того, будет ли он использоваться в будущем. Лишь после этого осуществляется переход к варианту (движение вширь). Ниже показано дерево решений (граф допустимых вариантов ТП) (рис. 54).

При использовании метода случайного поиска принятие решения, на каком либо уровне (выбор вершины на j-ом уровне дерева решений), выполняется случайным образом. Следовательно, и вариант Т_j получается случайным образом.

Р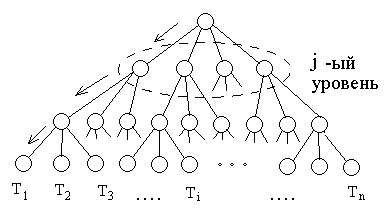 ис. 54. Стратегия поиска «сначала вглубь,

а затем вширь»

Другой стратегией является стратегия «сначала вширь, а затем вглубь» (направленный поиск, поэтапное отсечение решений). При этом на каждом уровне дерева решения выполняется оценка полученных решений, выбор лучшего решения и переход на следующий нижний уровень. Сложность применения данной методики заключается в том, что обычно невозможна точная оценка полученных на j-ом уровне решений, возникает проблема формирования критериев промежуточного отбора наиболее рациональных вариантов на различных уровнях. Используя приближенные и укрупненные оценки можно выбрать не одно решение, а несколько. На следующем уровне происходит уточнение отобранных решений с последующей уже более точной оценкой. Варианты решения не отвечающие. оценочным критериям отбрасываются. Таким образом, осуществляется направленный поиск варианта и первый найденный вариант должен быть близок к оптимальному. Однако из-за приближенных оценок, область оптимизации «размывается», и в нее попадают несколько вариантов технологических процессов, имеющих наилучшие оценки.

Если система оценок на каком-либо уровне слабо формализована, то необходимо вмешательство технолога в процесс автоматизированного проектирования (в режиме диалога), что дает возможность осуществления направленного поиска оптимального варианта, учитывающего, кроме того оперативную обстановку на предприятии. При этом, однако, в процесс проектирования вносится субъективный фактор.

Использование указанных направлений позволяет сократить количество проектируемых вариантов при экономически оправданных затратах на проведение расчетов с помощью ЭВМ.

Необходимо обратить внимание на то, что главным в проблеме оптимизации технологических процессов является структурная оптимизация как наиболее сильно влияющая на критерий оптимизации. Варьирование структурой процесса может в несколько раз изменить себестоимость ТП. Параметрическая оптимизация носит подчиненный характер, и ее влияние на себестоимость ТП не превышает 10 - 20 %.

Задачи проектирования технологических процессов (ТП) являются многовариантными (например, задачи выбора оборудования, инструмента, расчета режимов и т.д.). В разрабатываемом ТП число возможных комбинаций переходов, схем базирования, методов обработки и компоновок операций даже для простых деталей значительно, а для более сложных возрастает чрезвычайно.

Р азные варианты ТП изготовления одной и той же детали вследствие различий в структуре, применяемом оборудовании, инструменте, режимах и т.д., имеют различные выходные показатели: производительность, себестоимость, расход материалов, загрузку оборудования и др.

Наличие нескольких вариантов решения задачи (вариантов ТП) естественным путем приводит к задаче выбора наилучшего варианта. Таковым будет вариант ТП, обеспечивающий выполнение в конкретных производственных условиях все требования чертежа детали и дающий наилучшее значение выходных показателей. Такой технологический процесс носит название оптимального. Таким образом, задача проектирования ТП по своей природе является оптимизационной.

Следует отметить, что ТП оптимальный по одному критерию, может быть далеко не оптимальным по другому. Например, максимум производительности операции может не соответствовать минимуму ее себестоимости. Поэтому при постановке задачи проектирования оптимального ТП весьма важным является выбор критерия оптимальности.

Известен и применяется ряд различных критериев оптимальности, используемых для оптимизации как ТП в целом, так и при решении отдельных частных технологических задач. Наиболее часто используются следующие критерии оптимальности ТП: штучное время - (целевая функция ); производительность (целевая функция ); себестоимость детали (целевая функция ).

В целом же для постановки задачи оптимизации ТП (как и любой другой задачи оптимизации) необходимо сформировать математическую модель процесса обработки детали (сборки изделия), которая должна включать в себя:

1. критерий (критерии) оптимальности ТП;

2. целевую функцию;

3. систему ограничений;

4. четко определенные входные, выходные и внутренние параметры;

5. управляемый (варьируемый) параметр или параметры, которые выделяются из числа внутренних параметров.

После формирования математической модели необходимо определить (выбрать, разработать) метод решения задачи оптимизации.

Для сокращения вариантности ТП, а следовательно времени проектирования может использоваться прием, называемый «предпроектная оптимизация».

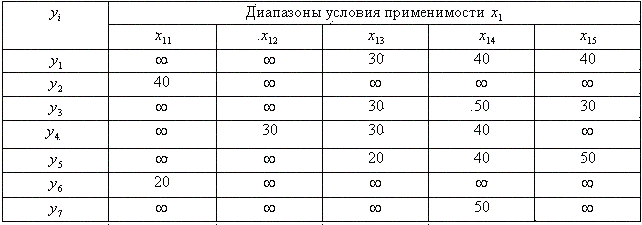
Пример. Выбор модели круглошлифовального станка. Множество возможных вариантов моделей круглошлифовальных станков определяется с помощью таблиц соответствий. Фрагмент такой таблицы приведен ниже (табл. 13).

Левая часть таблицы, обозначающая ее строки, представляет собой множество типовых решений. Верхняя часть таблицы, обозначающая ее столбцы, - условия применимости и их числовые значения. Центральная часть таблицы – булева матрица соответствий, в которой зафиксированы связи между решениями и определяющими их применимость значениями условий. Наличие связи обозначают единицей, отсутствие – нулем. Иногда вместо единицы применяют штриховку соответствующей клетки, вместо нуля клетку оставляют незаштрихованной.

Таблица 13

Фрагмент таблицы соответствий

 

По имеющемуся комплексу исходных данных из таблицы соответствий принимаются те решения, в строках которых булева матрица имеет единицы для всех значений факторов, входящих в условия применимости.

Н а базе таблиц соответствий строятся алгоритмы, позволяющие выбирать множество допустимых решений, из которых путем последовательного перебора выбираются наилучшие решения согласно тому или иному критерию оптимальности.

Но и при локализованной структурной оптимизации перебор и анализ всех допустимых решений, выбираемых из таблиц соответствий, занимает большое время. Для сокращения времени счета при структурной оптимизации с использованием таблиц соответствий производят так называемую предпроектную оптимизацию на стадии разработки информационного обеспечения. Для этого используют графики соответствий.

Построим график соответствий для одного из условий применимости, например, для первого – см. табл. 13. Критерий оптимизации – себестоимость С, соответственно, целевая функция С  min. Примем - типовые решения (здесь – модели станков), - диапазоны условий применимости. Пусть количество типовых решений (моделей станков) равняется не трем, а семи, количество диапазонов в первом условии применимости – пять.

График соответствий показан на рис. 55.

Соединяя линией решения, имеющие минимальную себестоимость, получаем линию минимальной себестоимости. Решения, лежащие на этой линии, называют предпочтительными.

 

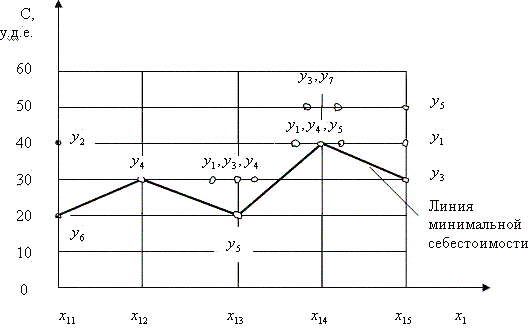
Рис. 55. График соответствий и линия минимальной себестоимости

Построим теперь таблицу соответствий, в которой единицы заменены штриховкой и предпочтительные решения выделены звездочками – см. табл. 14.

Таблица 14

Таблица соответствий для первого условия применимости

 

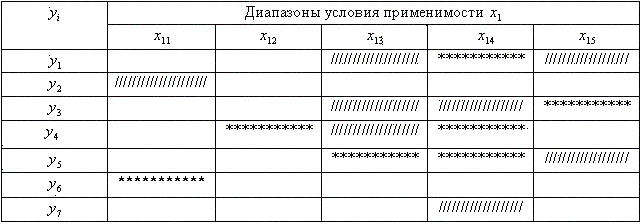
Другими словами в таблице штриховкой показаны технически возможные решения, звездочками – экономически эффективные решения.

Поиск решений в таблице соответствий сначала осуществляется по предпочтительным решениям. В случае отсутствия подходящего предпочтительного решения поиск производится по оставшимся допустимым.

Такой подход эффективен для случаев наличия экстремума целевой функции. Но в ряде случаев решение получается неопределенным. Так, например, в нашем случае для диапазона условия применимости имеется несколько эффективных решений.

Следующим шагом в развитии предпроектной оптимизации является переход от булевых матриц соответствий к оценочным матрицам. В этом случае в соответствующих клетках матрицы соответствий проставляются значения себестоимости с графика соответствий (табл. 15).

Подобные матрицы заполняются для всех условий применимости.

Алгоритм поиска оптимального решения по оценочной матрице состоит в поиске одноименной строки в оценочных матрицах для всех диапазонов условий применимости, обеспечивающей наименьшую сумму затрат для данного условия задачи.

Р ассмотренная процедура повторяется для каждого уровня проектирования, приводя в конечном итоге к варианту с оптимальной структурой.

Таблица 15

Оценочная матрица