7.3. Математическое моделирование

при автоматизированном проектировании

технологических процессов

 

В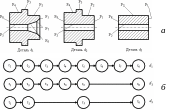 ыполнение проектных процедур при автоматизированном проектировании основано на оперировании с математическими моделями.

Математическая модель технологического процесса – это система математических объектов (чисел, переменных, множеств, графов, матриц и т.д.) и отношений между ними, отражающая некоторые свойства технологического процесса.

В САПР технологических процессов находят применение как структурно – логические, так и функциональные ММ.

Структурно - логические ММ подразделяются на табличные, сетевые и перестановочные.

Эти модели представляются в виде графа, который определяет состав и последовательность (маршрут) выполнения этапов, операций, переходов и рабочих ходов при обработке или сборке изделия. Вершины графа соответствуют элементам технологического процесса (этапам, операциям, переходам, рабочим ходам), а ребра или дуги графа характеризуют последовательность выполнения элементов технологического процесса. ММ технологического процесса может быть также описана матрицей свойств детали.

 Табличная модель описывает одну конкретную структуру технологического процесса. В табличной модели каждому набору условий соответствует единственный вариант проектируемого технологического процесса. Поэтому табличные модели используют для поиска стандартных, типовых или готовых проектных решений.

Пример. При обработке группы деталей на токарном автомате последовательность обработки их поверхностей устанавливается с помощью табличных моделей. Каждая деталь (рис. 45) имеет поверхности с определенными свойствами :

.

Рис. 45. Табличные модели проектирования маршрута обработки деталей: а – группа деталей со свойствами F_i; б – графы взаимосвязи операторов (технологических переходов) для деталей; τ₁ - подрезка торца; τ₂, τ₃, τ₄ - точение наружных цилиндрических поверхностей; τ₅ - сверление; τ₆ - зенкерование; τ₇ - зенкование; τ₈ - отрезка.

Таблица 10
Связи между совокупностями свойств деталей и операторами (технологическими переходами)
τi /Fi”	F1”	F2”	F3”
τ1	1	1	1
τ2	1	1	1
τ3	1	1
τ4	1	1
τ5	1	1	1
τ6	1
τ7	1
τ8	1	1	1

Т абличная модель может быть представлена в форме графа (рис. 45), но для выражения данных об обработке деталей на данной операции на языке, понятном компьютеру, удобном для программирования, она быть удобно описана в виде двух таблиц или матриц (табл. 10 и 11), которые легко превращаются в массивы.

Сетевые и перестановочные модели применяют для получения типовых, унифицированных и индивидуальных проектных решений. Наличие в них вариантов позволяет производить оптимизацию технологических процессов.

Сетевая модель описывает множество структур технологического процесса, отличающихся количеством и (или) составом элементов структуры при неизменном отношении порядка.

Таблица 11

Связи между свойствами поверхностей деталей

и операторами (технологическими переходами)

τi / Fi	F1	F2	F3	F4	F5	F6	F7	F8
τ1	1
τ2		1
τ3			1
τ4				1
τ5					1
τ6						1
τ7							1
τ8								1

Примечание: логическая единица обозначает наличие связи.

С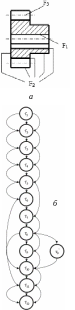 труктура элементов сетевой модели описывается ориентированным графом, не имеющим ориентированных циклов. В модели может содержаться несколько вариантов проектируемого технологического процесса, однако во всех вариантах порядок элементов одинаков.

Пример. Сетевая модель технологического проектирования маршрута обработки детали «Зубчатое колесо», эскиз которой представлен на рис. 46, а; граф взаимосвязи операторов (технологических операций) по возможной последовательности их выполнения изображен на рис. 46, б.

Граф можно представить в виде матрицы (массива). А массивы являются неизменными атрибутами любого языка программирования.

Кроме данного графа сетевая модель включает в себя таблицу связей свойств поверхностей детали и операторов технологического процесса - табл. 12.

Рис. 46. Сетевая модель технологического проектирования маршрута обработки зубчатого колеса: а – зубчатое колесо со свойствами F_i; б – граф взаимосвязи операторов по возможной последовательности их реализации (τ_i - операции)

Перестановочная модель описывает множество структур технологического процесса, отличающихся количеством и (или) составом элементов структуры при изменении отношения порядка.

Отношения порядка в этих моделях задаются с помощью графа, содержащего ориентированные циклы.

Таблица 12
Связи между свойствами поверхностей детали и операторами технологического процесса
τi / Fi	F1	F2	F3
τ1	1	1
τ2	1
τ3		1
τ4		1
τ5			1
τ6			1
τ7	1	1	1
τ8	1
τ9			1
τ10			1
τ11	1	1	1
τ12	1	1	1

П
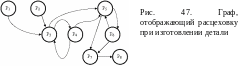
ример. Расцеховка при изготовлении изделия (рис. 47). Через P₁, P₂,…, P₈ обозначены цеха: P₁ – литейный; P₂ – кузнечный; P₃ – механический; P₄ – термический; P₅ – механосборочный; P₆ - общей сборки; P₇ – испытательный; P₈ – упаковочный. Такая модель состоит из множества устанавливаемых элементов и наборов условий базирования (возможности соединения и доступа при осуществлении сборки).

Функциональные модели отражают физические процессы, протекающие в технологических системах (например, в функционирующем оборудовании, инструменте, приспособлении и обрабатываемой заготовке). Характерным примерами функциональных моделей являются математические модели, используемые при расчете и оптимизации режимов резания.

При технологическом проектировании наиболее распространены дискретные модели, переменные которых дискретны, а множество решений счетно. В большинстве случаев проектирования технологических процессов используют статические модели, уравнения которых не учитывают инерционность процессов в объекте.

По форме связей между выходными, внутренними и внешними параметрами при обработке или сборке изделий различают модели в виде системы уравнений (алгоритмические) и модели в виде явных зависимостей выходных параметров от внутренних и внешних (аналитические).