5.3.1.2. Метод спирального координатного спуска

Отличается от рассмотренного выше лишь тем, что шаг h меняется каждый раз при переходе от поиска минимума по одной переменной к поиску минимума по другой переменной. В трехмерном пространстве это напоминает спуск во впадину по спирали. Обычно метод дает некоторое сокращение времени поиска.

5.3.1.3. Метод Хука и Дживса

Осуществляет два типа поиска – исследующий поиск и поиск по образцу. Первые две итерации процедуры показаны на рис. 31. При заданном начальном векторе х₁ исследующий поиск по координатным направлениям приводит в точку х₂. Последующий поиск по образцу в направлении х₂ - х₁ приводит в точку у. Затем исследующий поиск, начинающийся из точки у, дает х₃. Следующий этап поиска по образцу вдоль направлений х₃ – х₂ дает у*. Затем процесс повторяется.

Р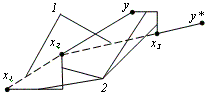 ис. 31. Иллюстрация двух первых итераций метода Хука и Дживса: 1 – поиск по образцу; 2 – исследующий поиск

5.3.1.4. Метод Розенброка

При варианте метода с применением одномерной оптимизации на каждой итерации процедура осуществляет итеративный поиск вдоль n независимых ортогональных направлений, целевая функция последовательно минимизируется вдоль каждого из направлений. Когда получена новая точка в конце итерации, строится новое множество ортогональных векторов.

5.3.1.5. Метод минимизации по правильному

симплексу

Правильным симплексом в пространстве Е_n называется множество из n + 1 равноудаленных друг от друга точек (вершин симплекса). Отрезок, соединяющий две вершины, называется ребром симплекса. В пространстве Е₂ (двумерном) правильным симплексом является совокупность вершин равностороннего треугольника, а в трехмерном Е₃ – правильного тетраэдра. Координаты вершин симплекса можно аналитически определить через известную (базовую) вершину.

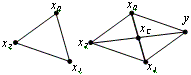
В алгоритме симплексного метода используется следующее важное свойство правильного симплекса: по известному симплексу можно построить новый симплекс путем отражения какой-либо вершины х₀ симметрично относительно центра тяжести х_С остальных вершин (х₁, х₂) симплекса (рис. 32). В результате получаем новый симплекс с тем же ребром и новую вершину у (положение которой также можно аналитически определить через старую), т.е. происходит перемещение симплекса в пространстве.

Рис. 32. Построение нового симплекса в двумерном пространстве Е₂ отражением точки х₂

Поиск точки минимума функции с помощью правильных симплексов производится следующим образом. На каждой итерации сравниваются значения функций в вершинах симплекса. Затем производится описанная выше процедура отражения для той вершины, значение функции в которой наибольшее. Если в отраженной вершине получается меньшее значение функции, то переходят к новому симплексу. В случае если попытка отражения не приводит к уменьшению функции, то сокращают длину ребра симплекса, например, вдвое и строят новый симплекс с этим ребром. В качестве базовой выбирают ту вершину старого симплекса, в которой функция принимает минимальное значение. Поиск заканчивают, когда ребро симплекса или разность между значениями функции в вершинах симплекса становятся достаточно малыми.

Алгоритм минимизации по правильному симплексу можно модифицировать, добавив к процедуре отражения при построении нового симплекса процедуры сжатия и растяжения ( рис. 33). А именно, положение новой вершины находится сравнением и выбором наименьшего значения целевой функции в пробных точках, лежащих на медиане, проведенной из отражаемой вершины на различном расстоянии от нее. Однако при деформациях утрачивается свойство правильности симплекса.