4.4. Методы конечных элементов и разностей

При формировании соединения в процессе сварки происходит сложное взаимодействие различных явлений, оказывающих существенное влияние на качество получаемого соединения: протекание электрического тока через сварное соединение; распространение теплоты; диффузия компонентов сплава; структурные, фазовые и химические превращения; образование остаточных напряжений и деформаций.

Изучение данных процессов возможно на натурных образцах, однако моделирование МКЭ позволяет снизить трудоемкость работ, ограничив количество экспериментальных исследований, которые применяются в этом случае для проверки и корректировки полученной математической модели.

ММ объектов часто описывают дифференциальными уравнениями. Для получения единственного решения необходимо задавать краевые условия. Сведения об искомых непрерывных функциях на границах рассматриваемых областей – граничные условия, а в случае нестационарных задач - значения этих же функций в начальный момент времени - начальные условия. Исходное дифференциальное уравнение в частных производных вместе с краевыми условиями носит название краевой задачи и представляет собой ММ исследуемого объекта.

Точное решение краевых задач удается получить лишь для немногих частных случаев, поэтому общий способ их решения, в т.ч. и в САПР заключается в использовании различных приближенных моделей. Наиболее часто используются модели на основе интегральных уравнений и на основе метода сеток.

Основная идея построения моделей по первому методу заключается в переходе от исходного дифференциального уравнения в частных производных к эквивалентному интегральному, подлежащему дальнейшему преобразованию. Второй случай будет рассмотрен ниже.

4.4.1. Общая характеристика метода сеток

Сущность метода сеток состоит в аппроксимации искомой непрерывной функции совокупностью приближенных значений, рассчитанных в некоторых точках области – узлах. Совокупность узлов, соединенных некоторым образом формируют сетку.

Сетка является дискретной моделью области определения исходной функции.

Применение метода сеток позволяет свести дифференциальную краевую задачу к системе нелинейных в общем виде алгебраических уравнений относительно неизвестных узловых значений функции.

В общем случае алгоритм метода сеток состоит из трех этапов:

1 . построение стеки в заданной области (дискретизация задачи);

2. получение системы алгебраических уравнений относительно узловых значений (алгебраизация задачи);

3. решение полученной системы алгебраических уравнений.

Наиболее часто используют два метода сеток: метод конечных элементов (МКЭ) и метод конечных разностей (МКР). Они отличаются на этапах 1 и 2 алгоритма, на 3 этапе - практически идентичны.

4.4.2. МКЭ

МКЭ состоит в том, что все тело разбивают на некоторое количество частей (элементов) конечного (а не бесконечно малого) объема, простых по форме и внутреннему устройству, поэтому математическое описание каждого не вызывает затруднений. Условие стыковки записывают в виде алгебраических уравнений. Существует ряд методов родственных МКЭ: метод конечных разностей, метод граничных элементов и др. Каждый из них в чем-то превосходит МКЭ при решении определенного круга задач, однако МКЭ является более гибким и универсальным.

Для упрощения процедуры элемент обычно выбирают простой формы и описывают распределение потенциалов внутри него простой функцией (например, полиномом невысокого порядка). Поэтому при небольшом количестве элементов решение является весьма грубым, однако при измельчении элементов погрешность уменьшается, и решение неограниченно приближается к точному. Чем грубее и проще элементы, тем мельче они должны быть для достижения заданной точности. Следует выбирать элементы, дающие наименьшую погрешность при данных размерах и обеспечивающих ее быстрое убывание при уменьшении размеров.

Поскольку число элементов и порядок системы уравнений для сложных задач может достигать десятков тысяч, данный этап является наиболее трудоемким в МКЭ. Иногда намеренно усложняют элементы (повышают степень описывающих их полиномов) для сокращения их количества и снижения порядка системы уравнений.

Для решения данной задачи возможно также использование суперэлементной процедуры. При этом несколько элементов объединяют в один суперэлемент, исключая из системы уравнений неизвестные, описывающие внутренние границы между объединяемыми элементами, а учитывая границы между суперэлементами. После решения упрощенной системы уравнений возвращаются к внутреннему устройству суперэлемента и находят исключенные переменные. Таким образом, общее число операций не сокращается, но задача упрощается за счет ее разделения на несколько этапов. Сокращение расчетов может быть получено, если в модели много одинаковых суперэлементов, тогда часть операций можно не повторять.

Наиболее известные программные комплексы МКЭ - NASTRAN, ANSYS (рис. 15), а также специализированные для решения сварочных и других технологических задач – SYSWELD, MARC.

В России также работают над созданием программного обеспечения МКЭ, это комплексы: «СВАРКА», разработанный на кафедре сварки МГТУ им. Н.Э. Баумана (рис. 16 - 18); «АСТРА-С», реализующий метод поэтапного расчета сварных конструкций; «WELD3D» для осуществления процедуры суперэлементов и др.

В МКЭ исходная область определения функции разбивается с помощью сетки, в общем случае неравномерной, на отдельные подобласти – конечные элементы. Искомая непрерывная функция аппроксимируется кусочно-непрерывной, определенной на множестве конечных элементов (КЭ). Аппроксимация может задаваться произвольным образом, но чаще всего для этих целей используют полиномы, которые подбирают так, чтобы обеспечить непрерывность искомой функции в узлах на границах элементов.

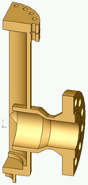
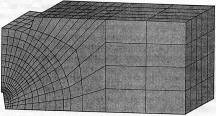
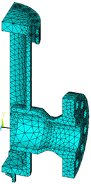
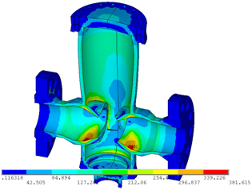
а б в

Рис. 15. Геометрическая (а), конечноэлементная (б) модель и поле напряжений (в) корпуса задвижки в ANSYS []

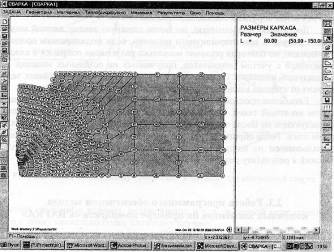
Рис. 16. Диалоговое окно комплекса «СВАРКА»

Р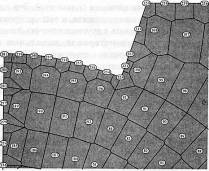 ис. 17. Фрагмент модели для расчета массопереноса

Пример. Расчет одномерного температурного поля.

К одному концу стрежня подводиться тепло, на другом происходит конвективный теплообмен с окружающей средой (рис. 19, а). Вдоль боковой поверхности стержень теплоизолирован. Искомое температурное поле является непрерывной функцией координаты х (рис. 19, б).

Рис. 18. Получение объемной модели из плоской

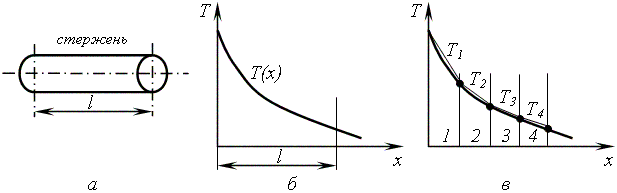
Рис. 19. Расчет одномерного температурного поля в МКЭ

В МКЭ стержень разбивается произвольным образом на КЭ, которые в данном случае являются отрезками неравной длины. На каждом элементе непрерывная функция аппроксимируется некоторой линейной зависимостью. Аппроксимирующая кусочно-линейная функция определяется через узловые значения Т₁ – Т_п, которые в общем виде сначала неизвестны и подлежат определению в МКЭ (рис. 19, в).

Д ля двумерных областей наиболее часто используют конечные элементы в форме треугольника и четырехугольника (прямоугольника, ромба и т.д.), при этом они могут иметь не только прямо-, но и криволинейные границы, что позволяет с достаточной степенью точности аппроксимировать границу любой формы. В случае трехмерных областей – тетраэдр, параллелепипед.

В общем случае МКЭ состоит из четырех этапов:

1. выделение конечных элементов (разбиение заданной области на КЭ);

2. определение аппроксимирующей функции для каждого элемента;

3. объединение КЭ в систему алгебраических уравнений;

4. определение узловых значений функции.

4.4.3. МКР

В МКР также строится сетка в заданной области, формируемая конечным множеством узлов. В узлах сетки определяются приближенные значения искомой функции. Совокупность узловых значений функции называется сеточной функцией.

Используются, как правило, регулярные сетки, шаг которых постоянен или меняется по несложному закону. Для одномерных областей построение сетки практически не отличается от аналогичной процедуры в МКЭ (рис. 20).

Рис. 20. Построение сетки

в МКР

Расстояние между соседними узлами называется шагом сетки h_i = x_i – x_i+1 при i = 1,2,…,n. Для регулярной сетки h_i = const = 1(n -1), где n – количество узлов.

Для двумерной области подход к построению сетки другой (рис. 21). Область изменения функции прямоугольник. Оси х и у разбиваются на отрезки, которые являются шагами сетки по соответствующим направлениям, через точки деления проводят прямые параллельные осям. Совокупность точек пересечения (узлов) образует сетку. Соседние узлы – расстояние между которыми равно шагу сетки по одной из осей.

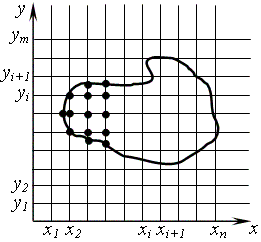
Рис. 21. Пример разбиения на КЭ двумерной области в МКР

Способ построения не меняется и в том случае, если область произвольной формы (рис. 21). Узлы сетки, попавшие внутрь области – внутренние. Точки пересечения прямых сетки с границей области называются граничными узлами. Даже для постоянных шагов сетки по осям х и у в области имеются граничные узлы, отстоящие от ближайших к ним внутренних на расстояние меньше шага по соответствующему направлению. Сетка для двумерной области в общем случае является нерегулярной, причем особенности геометрии учитываются только в околограничных участках (узлах).

Программные средства, позволяющие конструировать абстрактную модель и разбивать ее на конечные элементы, называются препроцессорами (preprocessors). Проанализировав каждый элемент, компьютер собирает результаты воедино и представляет их в визуальном формате. Например, области с высоким напряжением могут быть выделены красным цветом. Программные средства, обеспечивающие визуализацию, называются постпроцессорами (postprocessors).

Более подробно с процедурами МКЭ и особенностями их реализации при расчете сварных конструкции можно ознакомиться в соответствующей литературе [1, 18, 19, 23, 55, 56, 58, 62], а также в Internet [70 – 72] и многих других источниках.