4.2. Математические модели

Если проектная процедура включает создание математической модели (ММ) и оперирование с ней с целью получения полезной информации об объекте, то говорят о математическом моделировании.

К ММ предъявляют требования по универсальности, адекватности, точности и экономичности.

Степень универсальности ММ характеризует полноту отображения в модели свойств реального объекта. ММ отражает лишь некоторые свойства объекта. Так, большинство ММ, используемых при функциональном проектировании, предназначено для отображения протекающих в объекте физических и информационных процессов, при этом не требуется описание геометрических размеров, формы и др. параметров (например, описание резистора через закон Ома).

Т очность ММ оценивают степенью совпадения значений параметров реального объекта и значений тех же параметров, рассчитанных с помощью оцениваемой ММ.

Адекватность ММ – способность отобразить заданные свойства объекта с погрешностью не выше заданной.

Экономичность ММ – характеризуется затратами вычислительных (аппаратных) ресурсов (машинного времени, памяти и т.д.) на ее реализацию. Чем они меньше, тем экономичнее модель. Вместо данных значений, зависящих не только от свойств модели, но и от особенностей ЭВМ, часто используют другие величины, например, среднее количество операций, выполняемых при одном обращении к модели (или в единицу времени), размерность системы уравнений, количество используемых в модели параметров и т.д.

Требования высокой точности, степени универсальности, широкой области адекватности, с одной стороны, и высокой экономичности, с другой, противоречивы. Это обстоятельство обуславливает применение с САПР широкого спектра ММ.

Классификация ММ приведена в табл. 3.

Структурные ММ предназначены для отображения структурных свойств объекта. Различают топологические и геометрические структурные ММ.

В топологических ММ отображаются состав и взаимосвязи элементов объекта. Применяют для описания объектов, состоящих из большого количества элементов (задачи компоновки – привязки конструктивных элементов к определенным пространственным позициям или к относительным моментам времени; составления ТП – графы, таблицы, списки, матрицы и т.д.).

Геометрические ММ отражают геометрические свойства объектов (совокупность сведений, однозначно определяющих его форму), в них дополнительно к сведениям о взаимном расположении элементов содержаться сведения о форме деталей (уравнения линий, поверхностей; алгебраические соотношения, описывающие области, составляющие тело объекта; графы; списки; таблицы; описания на специальных графических языках). Теоретической основой для создания геометрических моделей являются аналитическая геометрия, теория множеств, дифференциальная геометрия, теория графов, алгебра, логика. ГММ разделяются на дву- и трехмерные.

Таблица 3

Виды математических моделей

Признак классификации	Математические модели
1. Характер отображаемых свойств объекта	Структурные; функциональные
2. Принадлежность к иерархическому уровню	Микро-; макро-; метауровня
3. Степень детализации описания внутри одного уровня	Полные; макромодели
4. Способ представления свойств объекта	Аналитические; алгоритмические; имитационные
5. Способ получения модели	Теоретические; эмпирические

В алгоритмах геометрического проектирования фигурируют геометрические объекты, являющиеся исходными данными, промежуточными и окончательными результатами конструирования. Детали и узлы конструкции имеют самые разнообразные геометрические характеристики, например, поверхность детали характеризуется микрогеометрией (шероховатость, отклонение формы и размеров) и макрогеометрией (параметрами, определяющими форму и положение в пространстве). Через геометрические характеристики детали вычисляются исходные геометрические параметры для функциональных моделей: масса, центр масс, моменты инерции, жесткость и демпфирование. Геометрические параметры определяют конструктивные элементы детали (шпоночный паз, канавку, взаимодействие деталей и т.д.). Кроме того, эти параметры связаны с технологическими характеристиками, необходимыми для изготовления детали и сборки узла.

П ри геометрическом моделировании ГМ применяются для описания геометрических свойств объекта конструирования (формы, расположения в пространстве); решения геометрических задач (позиционных и метрических); преобразования формы и положения геометрических объектов; ввода графической информации; оформления конструкторской документации.

Выделяют следующие разновидности геометрических моделей:

- аналитические – уравнения поверхностей и линий (контуры и поверхности деталей) как в прямоугольной, так и в полярной системе координат; служат основой для описания элементарных геометрических объектов (ЭГО), на основе которых могут быть получены составные геометрические объекты (каждый участок составной геометрической модели или контура описывается своим уравнением, а описание общей модели становится кусочно-аналитическим).

- алгебраические (алгебрологические) – система логических выражений (уравнений), отражающих условия принадлежности точек к внутренним пространственным областям тел (обеспечивают задание плоских фигур и трехмерных тел). Для сложных поверхностей аналитические и алгебраические ММ слишком громоздки, их трудно получать и неудобно использовать, поэтому область применения ограничиваю плоскими поверхностями второго порядка;

Пример. Геометрический объект, образованный из типовых геометрических объектов (рис. 14). Области D₁ – D₄ на плоскости х0уопределяются с помощью неравенств следующим образом:

.

Тогда геометрический объект D₀ (заштрихованная область) может быть записан с помощью соотношений выше и логического выражения

.

Р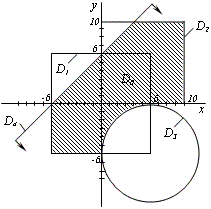 ис. 14. Пример описания области (например, при раскрое листового материала) посредством пересечения и объединения типовых геометрических объектов в алгебраическую модель

- каркасные – представляют собой каркасы – конечные множества элементов, например, точек или линий (кривых), принадлежащих моделируемой поверхности (совокупность узлов, соединенных между собой отрезками - связями), получаемые, например, МКЭ и МКР. Используются при описании поверхности в прикладной геометрии. При этом одним из основных понятий является понятие определителя поверхности – совокупность условий, задающих поверхность. Определитель состоит из геометрической и алгебраической частей. В первую входят геометрические объекты, а также параметры формы и положения, вторая задается правилами построения точек и линий поверхности при непрерывно меняющихся параметрах геометрической модели. Для воспроизведения ГМ на станках с ЧПУ, ЭВМ и печатающих устройствах их приходится задавать в дискретном виде. Дискретное множество значений параметров определяет дискретное множество линий поверхности, которое в свою очередь называется дискретным каркасом поверхности. Для получения непрерывного каркаса из дискретного необходимо произвести аппроксимацию поверхности. Непрерывные каркасы могут быть получены перемещением в пространстве плоской или пространственной линии, такие ГМ называются кинематическими;

- кинематические – поверхность представляется в параметрическом виде, путем перемещения в трехмерном пространстве образующей (кривой), по некоторой направляющей. Примерами простых кинематических моделей поверхностей являются поверхности вращения (эллипсоид, тор) и линейчатые поверхности (порожденные семейством прямых - цилиндрическая, коническая). Для образования поверхностей кинематическим методом могут использоваться обводы, т.е. кривые, составленные из дуг, описываемых различными уравнениями;

- канонические модели используют в тех случаях, когда удается выделить параметры, однозначно определяющие геометрический объект, и в то же время имеющие простую связь с его формой (например, для окружности такими параметрами являются координаты центра и радиус);

- рецепторные геометрические модели в своей основе имеют приближенное представление геометрического объекта в плоскости или пространстве рецепторов. В области рецепторов строится прямоугольная решетка или сеть. Каждая клетка сети или решетки рассматривается как отдельный рецептор, который может иметь состояние 0 или 1. Рецептор считается возбужденным (значение 1), если он включается в контур плоской или пространственной области. Каждый плоский или пространственный геометрический объект может быть описан двухмерной или трехмерной матрицей, состоящей из нулей и единиц;

- проекционные - трехмерные модели представленные как совокупность видов: главного, вида сверху и вида слева;

- полигональные (поверхностные) модели описываются поверхностями (плоскостями, по­верхностями вращения и др.). С помощью полигональной модели можно описать любую поверхность технического объекта. Это реа­лизуется путем аппроксимации поверхностей многогранником. Чем больше число граней, тем меньше отклонение от действительной формы объекта. Если объект представлен полигональной моделью, то всегда можно определить область между контурными элемента­ми этого объекта. Над полигональными моделями ГО можно вы­полнять логические операции объединения, вычитания, пересечения;

- объемные (твердотельные) - формируются из элементарных объек­тов (базисных тел) с использованием логических операции объе­динения, вычитания, пересечения. Объемные модели пред­ставляют объекты с обеспечением логической связности информа­ции, в частности благодаря введению понятия о материале и его физических свойствах (плотности, теплопроводности и др.). По та­ким моделям можно построить не только графические изображения (виды, разрезы, сечения), необходимые для чертежа изделия, но и рассчитать его массовые и инерционные характеристики, такие, как мас­са, объем, центр тяжести, моменты инерции и др.;

- составные - объемные тела и геометрические изображения, образованные из более простых объектов с использованием логических булевых операции объединения, пересечения и вычитания;

- геометрические макромодели являются описаниями предварительно отобранных типовых геометрических фрагментов, с их помощью можно графически представить шестерни, детали ременных передач, резьбовые соединения, подшипники и т.д.

Функциональные ММ предназначены для отображения физических или информационных процессов, протекающих в объекте при его функционировании или изготовлении (системы уравнений, связывающие внутренние, внешние и выходные параметры) (поля напряжений, деформаций, давлений, температур).

О собенностью ММ на микроуровне является отражение физических процессов, протекающих в непрерывном пространстве и времени. Типичные ММ на микроуровне - дифференциальные уравнения в частных производных. В них независимыми переменными являются пространственные координаты и время. Возможности применения ММ на микроуровне ограничиваются отдельными деталями, попытки проанализировать с их помощью процессы в многокомпонентных средах, сборочных единицах требуют значительных вычислительных ресурсов.

На макроуровне используют укрупненную дискретизацию пространства по функциональному признаку, что приводит к представлению ММ на этом уровне в виде систем обыкновенных дифференциальных уравнений. Независимой переменной является время, в вектор зависимых переменных составляют фазовые переменные, характеризующие состояние укрупненных объектов (силы и скорости механических систем; напряжения и силы тока электрических; давление и расход гидравлических и пневматических). Такие модели применяются для анализа динамических и установившихся состояний.

На метауровне в качестве элементов принимают достаточно сложные совокупности деталей. Характеризуется большим разнообразием используемых ММ.

Структурные модели также делятся на модели различных иерархических уровней. При этом на низших иерархических уровнях преобладает использование геометрических моделей, на высших – топологических.

Полная ММ – модель, в которой фигурируют фазовые переменные, характеризующие состояния всех межэлементных связей (состояние всех элементов (параметров) проектируемого объекта).

Макромодель – ММ, в которой отображаются состояния значительно меньшего числа межэлементных связей, что соответствует укрупненному описанию объекта.

Данные понятия относительны и обычно используются для различения двух моделей, отражающих разную степень детальности описания свойств объекта.

Алгоритмические ММ выражают связи выходных параметров с параметрами внутренними и внешними в форме алгоритма.

Имитационная ММ – алгоритмическая модель, отражающая поведение исследуемого объекта во времени при заданных внешних воздействиях на объект.

Существуют формальные и неформальные методы получения ММ. Неформальные методы применяют на различных иерархических уровнях для получения ММ элементов. Эти методы включают:

- изучение закономерностей процессов и явлений;

- выделение существенных факторов;

- принятие допущений и их обоснование.

Их применение возможно для синтеза теоретических и экспериментальных ММ.

Теоретические ММ создаются в результате исследований процессов и их закономерностей, присущих рассматриваемому классу объектов и явлений.

Эмпирические ММ – в результате изучения внешних проявлений свойств объекта с помощью измерения и анализа параметров объекта или явления.

Формальные методы получения ММ применяют для формирования ММ систем при известных ММ элементов.

Для того чтобы что-то рассчитать, надо формализовать задачу, т.е. составить математическую модель, поскольку по своей природе математические методы можно применять не непосредственно к изучаемой действительности, а лишь к математическим моделям тех или иных явлений. Причем результаты исследований математических моделей представляют практический интерес только тогда, когда эти модели достаточно адекватно отображают реальные ситуации и достаточно совершенны.

П роцесс формирования математической задачи и алгоритма ее решения можно представить в виде следующих этапов:

1. изучение объекта – на этом этапе следует хорошо понять все особенности функционирования объекта, четко определить факторы, влияющие на его функционирование, их число и степень влияния, выбрать критерий оптимизации, отражающий цель рассматриваемой задачи; выбор свойств объекта, которые подлежат изучению и отражению в модели (определяет степень универсальности); сбор исходной информации о выбранных свойствах;

2. описательное моделирование – устанавливают и словесно фиксируют основные связи и зависимости между характеристиками процесса или явления с точки зрения оптимизируемого критерия;

3. математическое моделирование – переводят описательную модель на формальный математический язык (синтез структуры ММ), все условия записывают в виде соответствующей системы равенств и неравенств, а критерий оптимизации – в виде функции; после того как задача записана в математической форме, ее конкретное содержание перестает нас интересовать до момента проведения содержательного анализа получаемого решения, т.к. различные по своему содержанию задачи часто можно привести в одной и то же формальной математической записи;

4. выбор или создание метода решения – главное внимание обращают на полученную математическую структуру (постановку) задачи, и, исходя из нее, выбирают либо известный метод решения, либо некоторую модификацию известного метода, либо разрабатывают новый;

5. выбор или написание программы для решения на ЭВМ;

6. решение задачи на ЭВМ;

7. анализ полученного решения – оценка точности и адекватности ММ.

Шаги 1 – 7 могут повторяться многократно в процессе приближения к желаемому результату.

Анализ полученного решения бывает формальным (математическим) и содержательным. При формальном анализе проверяют соответствие полученного решения построенной ММ, т.е. производят проверку правильности введения исходных данных, функционирования программы, ЭВМ и т.д. При содержательном анализе проверяют соответствие полученного решения реальному объекту. В результате содержательного анализа в модель (словесную и математическую) могут быть внесены изменения, после чего рассмотренный процесс повторяют. Только после полного завершения анализа (формального и содержательного) модель может быть использована для расчета.

Следует иметь в виду, что в математическом программировании выделяют два вида решений: допустимое решение и собственно решение задачи.

Под допустимым решением понимают такой набор значений искомых величин (переменных), который удовлетворяет условиям – ограничениям задачи. Решением задачи из множества допустимых решений будет то, при котором целевая функция достигнет наибольшего (наименьшего) значения.

Пример. Когда впервые решали задачу о питании, то в качестве фактора оптимизации взяли минимуму затрат, а в условие – ограничение включили только требование по калорийности пищи. Решение задачи было таковым: питаться следует уксусом (входил в состав возможных продуктов питания), и калорийность обеспечена, и стоимость минимальна.