Контрольні запитання

1. Що таке незалежна та залежна змінна?

2. Що таке початкове значення?

3. Який зв'язок між порядком системи рівнянь та кількістю почат­кових значень.

4. Що таке стійкий розв’язок системи диференціальних рівнянь?

5. Як пов'язані кількість точок розв’язку на заданому відрізку та крок t?

6. Як впливає крок t на точність?

7. Чи є сенс у даному прикладі значно збільшувати кількість точок розв’язку після N=50?

Звіт повинен містити

1. Номер роботи, тему та результати досліджень відповідно до ходу роботи.

2. Відповіді на усі запитання у письмовій формі.

Практична робота №4

Тема: «Наближення функцій»

Мета роботи: Освоїти методику наближення функцій методом поліноміальної регресії (частина 1) та сплайнів (частина 2) за допомогою додатку MATHCAD.

Частина 1. Поліноміальна регресія

Методичні вказівки до першої частини роботи

1. Ввести допоміжну функцію vs:= 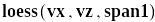, де vx та vz відповідно значення аргументу та функції, задані у табличному вигляді. Параметр span>0 вказує на величину відрізку аргументу, на якому відбувається локальне наближення функції.

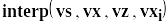2. повертає вектор, потрібний для , щоб знайти набор поліномів другого порядку, які найкращим чином наближають функцію на невеликих відрізках розміром span>0 навколо деяких точок vx, vy.

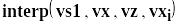3. повертає інтерпольоване значення y, яке відповідає х.

Введення даних

Вектор, заданий користувачем

Випадок 1: Span=0.6 Випадок 2: Span=7.0

Відображення результату

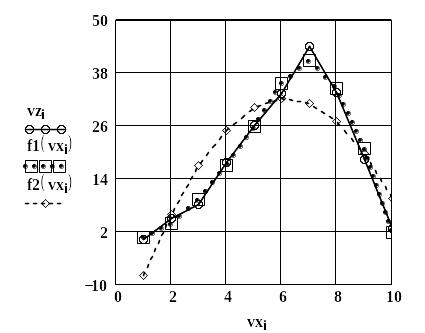
Рис. 1. Результат виконання поліноміальної регресії

Зробіть висновки: в якому разі точність інтерполяції вища за різними значеннями параметру span.

Одержіть у викладача таблицю вхідних даних vx, vz для кожної бригади та одержіть графік поліноміальної регресії для вказаного варіанту.

Частина 2. Кубічна сплайн-інтерполяція

Порядок виконання роботи

1. Створіть вектори vx та vy, які, відповідно, утримують координати x та y, через які треба провести кубічний сплайн. Елементи vx повинні бути розташовані у порядку зростання.

2. Обчисліть вектор vs:=cspline(vx,vy). Вектор vs містить другі похідні інтерполяційної кривої у заданих точках.

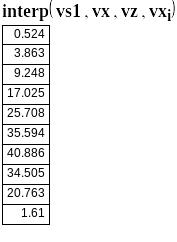
3. Щоб знайти інтерпольоване значення у довільній точці, наприклад х0, знайдіть interp(vs,vx,vy,x0), де vx,vy,x0 — вектори, які були описані раніше.

Зверніть увагу на те, що те ж саме можна було б одержати, обислюючи:

interp(cspline(vx,vy),vx,vy,x0)

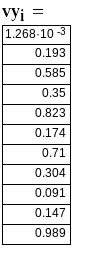
Випадковий вектор vy генерується за допомогою функції rnd(діапазон випадкових чисел). Значення аргументу співпадають з номером точки i.

Відображення результату

Одержання значення інтерпольованої функції у окремих точках

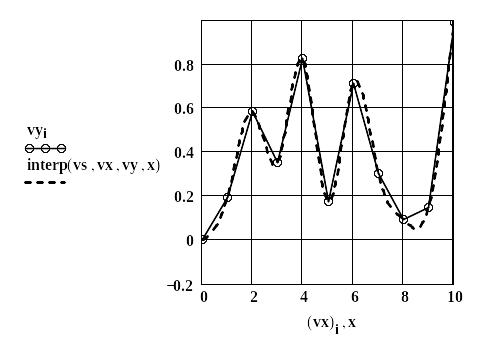
Рис. 2. Ілюстрація сплайн-интерполяції

Одержіть у викладача таблицю вхідних даних vx, vy для своєї бригади та побудуйте графік кубічної сплайн-інтерполяції для вказаного варіанту.

Контрольні запитання

1. Що таке наближення функцій?

2. Пояснити суть методу найменших квадратів.

3. Чим відрізняється апроксимація від інтерполяції?

4. Що таке апроксимація сплайнами?

Звіт повинен містити

5. Результати першої та другої частини роботи разом із формулами та графіками.

6. Відповіді на запитання.

Практична робота №5

Тема: «Перетворення Лапласа, Z-перетворення»

Мета роботи: засвоїти методику одержання прямого та зворотного перетворення Лапласа та Z–перетворення.

Методичні вказівки

Перетворення Лапласа існує у двох варіантах: неперервному та дискретному. Останнє одержало назву Z-перетворення. Для одержання зображення Лапласа у неперервному вигляді необхідно виконати операцію інтегрування заданої функції f(t) (яку називають оригіналом)з ваговою функцією у межах t(-∞, +∞),

якщо f(t) існує у цих межах та згаданий інтеграл може бути визначений. Функцію називають зображенням оригіналу . У зв’язку з цим можна зустрітися з наступною термінологією: простір оригіналу, тобто з незалежною змінною t, та простір зображень з незалежною змінною p. Цю змінну називають параметром перетворення Лапласа. Треба звикнути до того, що у різних літературних джерелах параметр перетворення Лапласа означають однією з літер: p або s. Параметр перетворення є комплексною величиною: .

У більшості практичних випадків допустимо вважати, що у межах t(-∞, 0), а також . Саме за таких умов, строго кажучи, допустимо використання перетворення Лапласа. Хоча на практиці результати досліджень з використанням перетворення Лапласа, як правило, без проблем можнп перенести й на випадок, коли умова порушується. Тому інтегрування достатньо виконати у межах t(0, +∞).

.

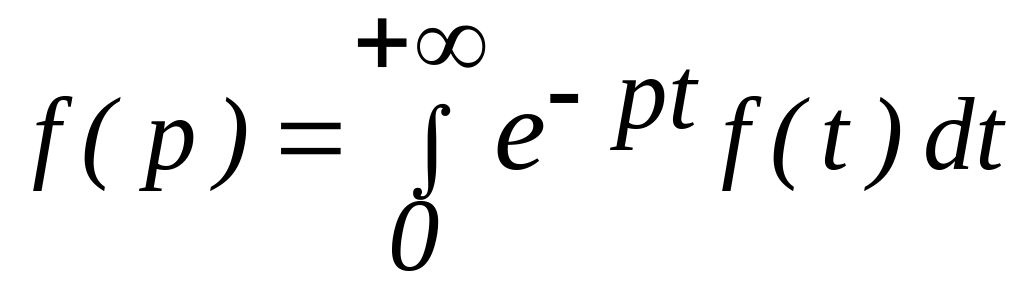Зворотне перетворення, тобто одержання за відомою достатньо складніше, бо вимагає знання теорії функцій комплексної змінної. Тому у даному разі не наводиться. Ознакою зворотного перетворення є вагова функція , що відрізняється знаком степені експоненти.

Для одержання зображення деяких функцій існують відповідні таблиці. Однак, практично ними майже не користуються. Розроблені методи, які дозволяють вирішувати велику кількість задач з теорії автоматичного керування, механіки, оптики (у тому числі голографії, оптичних дуже точних вимірювань), розпізнання образів та багато інших, які не потребують переходу до оригіналу. Задачі вирішуються у просторі зображень.

Для дискретних функцій існує дискретна форма перетворення Лапласа, або Z-перетворення, як пряме так і зворотне. У цьому випадку перетворення одержують аналогічно неперервній формі, заміняючи неперервний час дискретним, а інтеграл сумою.

У додатку Mathcad вбудована можливість у аналітичній формі одержувати як пряме, так і зворотне зображення Лапласа.

Для одержання відповідного перетворення необхідно взяти змінну, відносно якої необхідно виконати перетворення Лапласа у кут. Далі з головного меню вибрати відповідну операцію перетворення, як показано далі

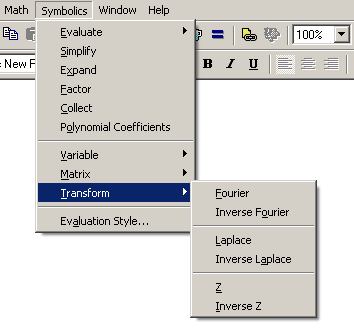
Оскільки одержання перетворень є підчас непростою операцією інтегрування, можливо з розкладанням у ряди різних видів, то результати, які можна побачити на екрані, можуть бути досить громіздкими. На цьому не треба особливо зосереджуватися, оскільки, як зазначалося, існують методи, які дозволяють обходитися без таких громіздких перетворень. Основна мета роботи – це ознайомлення перетворенням Лапласа достатньо простих функцій.