МІНСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ

КРИВОРІЗЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ

КАФЕДРА ІНФОРМАТИКИ, АВТОМАТИКИ ТА СИСТЕМ УПРАВЛІННЯ

Методичні вказівки

до виконання практичних робіт

з дисципліни

“Спецрозділи математики"

Ч.2 Чисельні методи

для студентів спеціальності

"Системи управління і автоматики" 6.050201

усіх форм навчання

м. Кривий Ріг

2013

Укладачі: доцент каф.ІАСУ, канд. техн. наук А.А. Жосан,

Відповідальні за випуск:

проф., д. т. н., В.М. Назаренко

Рецензент: доцент каф. МПЗ, канд. техн. наук П.С. Смолянський

Наведено вказівки та інструкції до виконання лабораторних робіт. Подані прості приклади алгоритмів, на основі яких студент повинен розробити алгоритм та програму розв’язання більш складної задачі.

Розглянуто на засіданні кафедри інформатики, автоматики і систем управління Протокол № від _______20____ р. Зав. кафедрою ______ Назаренко В.М.

Схвалено на вченій раді факультету інформаційних технологій Протокол № від _______20____ р. Декан факультету ______ Вербицький В.І.

Вступ

Інструкції до практичних робіт побудовані таким чином, що у більшості випадків, студентам надається базовий варіант задачі та приклад її вирішення. Після цього викладачем пропонується кілька варіантів для самостійного вирішення.

Викладач може надавати оцінку кожному з варіантів практичної роботи після чого робити висновок про її захист.

Інструкції та методичні вказівки до виконання практичних робіт існують у двох варіантах: у форматі WORD (електронний та паперовий) та у форматі MATHCAD (електронний варіант). Принципова різниця між ними полягає в тому, що у форматі MATHCAD можна реально виконати усі варіанти завдань. У форматі WORD надані лише інструкції до виконання робіт у текстовому вигляді. Це зроблено тому, що документи MATHCAD не завжди можна коректно вставити у документи WORD. Для коректного розміщення результатів роботи з середовища MATHCAD у середовищі WORD необхідно зберігати результати не тільки у форматі *.mcd, але також і з середовища MATHCAD (як звичайно з використанням Save As) у форматі *.rtf (для перенесення у середовище WORD).

Для друкування звіту з виконаних робіт рекомендується додержуватися наступного порядку:

1. Виконати роботу у файлі формату MATHCAD. Для цього необхідно набрати програму, як це наведено у даному посібнику, або використати електронний варіант роботи у форматі MATHCAD за вказівкою викладача. До імені електронного варіанту файлу MATHCAD обов’язково додати якісь символи (наприклад перші літери свого прізвища). Ця рекомендація надається з метою збереження файлу-зразку.

2. Результати перенести у інструкцію в форматі WORD до відповідної роботи. Допускається підготовка звіту також у форматі MATHCAD, але з обов’язковим виконанням наступних вимог.

3. До звіту необхідно (якщо це навіть не оговорено спеціально у інструкції до конкретної роботи) обов’язково включати номер, назву та тему роботи, тексти та умови бригадних та індивідуальних завдань та результати їх виконання, а також відповіді на всі запитання.

4. Роздрукувати текст виконаної роботи у вигляді окремого видання в електронному вигляді у форматі А4 з полями: зліва 2 см, згори та знизу 2 см, з правого боку 1 см, без титульного листа.

5. Номер та назву практичнної роботи, а також назву групи та прізвище студента обов’язково розмістити у верхньому колонтитулі, де буде проставлена оцінка за її виконання. У такому вигляді робота представляється до захисту.

6. В кінці семестру усі роботи збираються разом. До них додається титульний лист (не плутати з титульним листом даних інструкцій). Форма титульного листа надана у кінці тексту даних інструкцій.

7. Кожна бригада здає CD зі збереженими на ньому двома копіями виконаних робіт студентами бригади. Кожна копія включає: тексти звітів у форматах WORD (*.rtf) та MATHCAD (*.mcd) та титульні листи до кожного звіту.

8. На титульному листі виставляється остаточна оцінка.

Виконання практичної роботи поділяється на основні етапи:

1. Попередньої самостійної підготовки, яка включає озна­йомлення з умовою практичної роботи, виконання необхід­них аналітичних вправ.

2. Налагодження програми з використанням засобів нала­годження та одержання наведених в інструкції результатів.

3. Самостійного складання алгоритмів та програм у відпо­відності з наведеними варіантами задач та вирішення їх з наведенням результатів.

4. Відповіді в письмовій формі на наведені запитання.

5. Самостійного вирішення базової та індивідуальної задачі.

6. Оцінку за знання теорії головним чином у межах питань до даної роботи можна одержати без пред’явлення звіту. Ця оцінка виставляється викладачем у журналі. Але остаточний залік по роботі можна одержати лише після пред’явлення звіту у вказаній раніше формі.

7. Захист роботи. Викладач не приймає до остаточного захисту роботу, яка оформлена неналежним чином. У разі захисту роботи оцінка проставляється викладачем на першій сто­рінці звіту з кожної з робіт. Одна оцінка за знання теорії проставляється у чисельнику, за виконання спільних та індивідуальної роботи у знаменнику.

Примітки:

1. Що стосується захисту роботи, наведені в інструкціях запитання слід вважати не єдиними чи остаточними, а лише типовими. Під час захисту роботи студенту можуть бути задані різні варіанти запитань у відповідності з темою роботи.

2. Під час захисту окремих робіт, або складання заліку студент повинен бути готовим надати конспект лекцій.

3. Програми вирішення задач в умовах практичної роботи №1 повинні бути створені студентами. Мова програмування не обмежується (окрім Бейсіка).

4. Програми для виконання інших робіт подані у готовому вигляді в тексті даного посібника. Вони також можуть бути надані викладачем у форматі Mathcad.

Практична робота №1 Тема: «Розв’язання алгебраїчних та тригонометричних рівнянь методом половинного ділення та методом ітерацій»

Мета роботи: засвоїти методи визначення коренів рівнянь, ознайомитися з поняттям збігу числових рішень.

Порядок виконання роботи

1. Визначити аналітичним шляхом точний розв’язок рівняння

a*x+b=0

на відрізку -5≤x≤5. Прийняти при цьому a=-0.5, b=-1.

2. Розв’язати це рівняння методом половинного ділення та методом ітерацій. Точність розв’язку (похибку) задавати з ряду: 0.1; 0.05; 0.001. Перед використанням методу ітерацій перевірити умову збігу процесу розв’язку рівняння цим методом.

3. Порівняти знайдений розв’язок з точним та знайденими різними числовими методами.

4. Задано рівняння

на відрізку -1≤x≤5. Прийняти при цьому a=0.2, b=2, с=1.

5. Довести, що точний розв’язок дорівнює

x=-5ln(1/2).

6. Розв’язати це рівняння методом половинного ділення та методом ітерацій. Точність розв’язку (похибку) задавати з ряду: 0.1; 0.05; 0.001. Перед використанням методу ітерацій перевірити умову збігу процесу розв’язку рівняння цим методом.

7. Розв’язати рівняння за індивідуальним завданням викладача.

Вказівка

Індивідуальні задачі необхідно вирішувати обома методами. Але методом ітерацій лише в тому випадку, коли цей метод збігається. Тому рекомендується спочатку віднайти корінь методом половинного ділення і в цій точці перевірити умову збігу процесу розв’язку методом ітерацій. В разі виконання умови розв’язати задачу методом ітерацій. Якщо точний розв’язок аналітичним способом виявиться дуже складним, або неможливим, розв’язати задачу за допомогою відповідних програм.

Контрольні запитання та завдання

1. В чому пролягає метод половинного ділення?

2. Від чого залежить точність розв’язку цим методом?

3. Чи завжди процес вирішення методом половинного ділення збіга­ється?

4. В яких випадках розв’язок методом половинного ділення не може бути знайдено, навіть якщо воно існує?

5. Що треба змінити для поліпшення можливості одержання розв’язку?

6. Як методом половинного ділення обчислити положення екстремуму функції?

а) без зміни алгоритму шляхом деяких аналітичних зусиль;

б) шляхом корекції алгоритму.

7. Написати та пояснити умови збігу процесу розв’язку рівняння методом ітерацій.

8. Чи будь-яке алгебраїчне та тригонометричне рівняння можна розв’язати методом ітерацій?

9. Вказати на переваги та недоліки обох методів.

10. Який метод Вам більше до вподоби? Чому?

Звіт повинен містити

1. Результати підготовки до виконання роботи згідно з п.п. 1 та 5.

2. Блок-схеми алгоритмів та тексти програм.

3. Результати розв’язку спільних та індивідуальних задач з необхід­ними поясненнями.

4. Пояснення всіх особливостей індивідуальної задачі. Чому вона не вирішується методом ітерацій? Чому виникли проблеми з одер­жанням точного значення кореня аналітичним шляхом?

5. Короткі але змістовні відповіді на поставлені запитання у письмовій формі.

П рактична робота №2

Тема: «Обчислення коренів поліномів та власних чисел матриць»

Мета роботи: навчитися обчислювати корені характеристичних поліномів, власні числа, коефіцієнт обумовленості матриці, ознайомитися з поняттям коректності розв’язку задач.

Теоретичні відомості

Задача 1

Визначити корені поліному, який необхідно представляти у вигляді

=0,

де а — вектор коефіцієнтів поліному.

Приклад визначення коренів полінома, заданого вектором своїх коефіцієнтів а

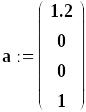
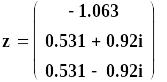
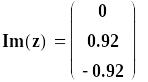
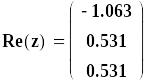
Заголовок циклу для побудови графіка коренів поліному

Рис.1. Відображення коренів поліному на комплексній площині

Задача 2

Визначити власні числа матриці М

Приклад визначення власних чи сел. матриці М

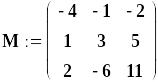
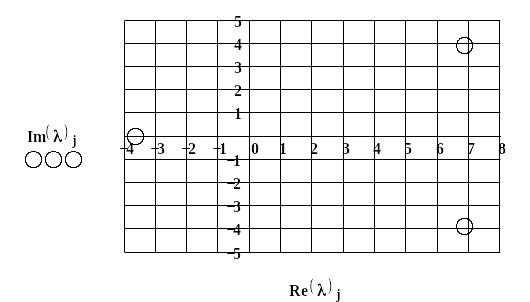
Рис.2. Відображення власних чисел матриці на комплексній площині

Хід роботи

1. Знайти корені поліному у відповідності із завданням викладача.

2. Знайти власні числа матриці та відповідного їй поліному за завданням викладача.

3. Написати однорідне диференціальне рівняння, яке відпо­відає даному поліному.

4. Написати поліном однорідного різницевого рівняння та саме рівняння, яке відповідає даному поліному. Необхідні для цього дані запросити у викладача.

5. Обчислити значення числа (коефіцієнта) обумовленості заданої матриці.