1. Пропорциональные отрезки в круге (доказать теоремы о пересекающихся хордах, пересекающихся секущих, секущей и касательной, проведенных из одной точки к окружности.

Т еорема 1 (следствие из теоремы о пропорциональных отрезках в прямоугольном треугольнике). Перпендикуляр, опущенный из какой-либо точки окружности на диаметр, есть средняя пропорциональная величина между отрезками, на которые основание перпендикуляра делит диаметр, а хорда, соединяющая эту точку с концом диаметра, есть средняя пропорциональная величина между диаметром и прилежащим к хорде отрезком диаметра.

ABC = 90 - вписанный,

опирающийся на диаметр.

 АВС – прямоугольный,

BD  AC, следовательно,

BD – высота, проведенная к гипотенузе.

Тогда на основании теоремы о пропорциональных отрезках в прямоугольном треугольнике:

Т еорема 2 (об отрезках пересекающихся хорд). Если через какую-либо точку внутри круга проведены хорда и диаметр, то произведение отрезков хорды равно произведению отрезков диаметра.

Дано: О – окружность;

Доказать:

Доказательство:

-

(по первому признаку подобия).

Следствие. Если через точку, взятую внутри круга, проведено сколько угодно хорд, то произведение отрезков каждой хорды есть величина постоянная для всех хорд.

Т еорема 3 (об измерении угла между хордой и касательной). Градусная мера угла, образованного хордой и касательной к окружности, проведенной через один конец хорды, равна половине градусной меры дуги, заключенной между сторонами угла.

Дано: О – окружность; AB – касательная, ВС – хорда.

Доказать:

Доказательство:

ВО  АВ - (по свойству касательной).

Т еорема 4 (об отрезках секущей и касательной). Если из точки, взятой вне круга, проведены к нему какая-либо секущая и касательная, то произведение секущей на ее внешнюю часть равно квадрату касательной. При этом считается, что секущая ограничена второй точкой пересечения, а касательная – точкой касания.

Дано: О – окружность; AB – касательная, AD – секущая.

Доказать:

Доказательство:

- (по первому признаку подобия).

Следствие. Если из точки М, взятой вне круга, проведены к нему сколько угодно секущих, то произведение каждой секущей на ее внешнюю часть есть число постоянное для всех секущих, так как для каждой секущей это произведение равно квадрату касательной, проведенной из точки М.

2. Вывод формулы для вычисления суммы внутренних углов выпуклого многоугольника.

Определение 1. Ломаной линией называется конечная последовательность отрезков, такая, что один из концов первого отрезка служит концом второго, другой конец второго отрезка служит концом третьего и т. п.

Отрезки, составляющие ломаную линию, называются звеньями. Соседние отрезки не лежат на одной прямой. Если концы ломаной совпадают, то она называется замкнутой. Ломаная может пересекать сама себя, касаться сама себя и налегать сама на себя. Если таких особенностей у ломаной нет, то она называется простой.

Определение 2. Простая замкнутая ломаная вместе с частью плоскости, ограниченной ею, называется многоугольником.

С ама ломаная при этом называется границей многоугольника, звенья ломаной – сторонами многоугольника, концы звеньев – вершинами многоугольника. Две соседних стороны многоугольника образуют угол. Число углов в многоугольнике равно числу сторон. У каждого многоугольника есть углы меньше 180°. Стороны и углы многоугольника называют элементами многоугольника.

Отрезок, соединяющий две несоседние вершины многоугольника, называется диагональю. В любом n-угольнике можно провести n-2 диагонали.

Определение 3. Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, содержащей его сторону. Многоугольники, не отвечающие этому условию, называются невыпуклыми.

Теорема о сумме внутренних углов выпуклого многоугольника. Сумма углов выпуклого многоугольника равна (n – 2)∙180°.

Доказательство:

С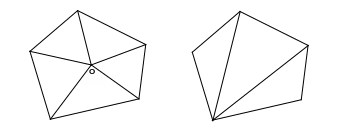 пособ 1: Возьмем внутри выпуклого многоугольника Р произвольную точку О и соединим ее со всеми вершинами многоугольника. Образуется n треугольников, сумма углов каждого из которых равна 180°. Углы при вершине О в сумме дают полный угол 360° = 2∙180°. Поэтому сумма углов многоугольника равна n∙180° - 2∙180° = (n – 2)∙180°.

Способ 2: Проведем все возможные диагонали из одной вершины выпуклого многоугольника. Они разобьют многоугольник на n – 2 треугольника. Сумма внутренних углов выпуклого многоугольника складывается из сумм внутренних углов получившихся треугольников, поэтому равна (n – 2)∙180°.

Билет № 4.