1. Взаимное расположение прямой и окружности. Характерное свойство касательной. Признак касательной. Доказать.

И сследуем взаимное расположение окружности с центром в точке О и прямой.

1) Прямая p пересекает окружность в двух точках и называется секущей. При этом расстояние от центра окружности до секущей p OK < R. Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки.

2) Прямая n касается окружности в одной точке В и называется касательной. При этом расстояние от центра окружности до касательной n OB = R. Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку.

3) Прямая m не имеет общих точек с окружностью. При этом расстояние от центра окружности до прямой m OC > R. Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек.

Определение 1. Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности.

Т еорема 1 (о характерном свойстве касательной). Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.

Доказательство:

Пусть прямая p касается окружности в точке А. Допустим, что прямая p не перпендикулярна ОА.

Проведем ОВp. Отложим на прямой p отрезок ВС = ВА. Тогда ΔАОВ = Δ СОВ как прямоугольные по двум катетам:

 OA = OC  точка С так же лежит на окружности, что противоречит условию. Следовательно, ОАp.

Теорема 2 (признак касательной, обратная). Прямая, проходящая через точку окружности и перпендикулярная ее радиусу, проведенному в эту точку, касается окружности.

Доказательство:

Возьмем любую точку А на окружности и проведем радиус ОА. Затем проведем прямую p, проходящую через точку А и перпендикулярную радиусу ОА. Любая точка В прямой p, отличная от точки А, удалена от О больше чем на радиус, поскольку наклонная ОВ длиннее перпендикуляра ОА. Следовательно, точка В не лежит на окружности. Значит, точка А − единственная общая точка прямой и окружности. Следовательно, прямая p является касательной к окружности.

2. Пропорциональные отрезки в трапеции.

1 . Отрезок, параллельный основаниям трапеции.

Пусть M₁N₁ II AD и AM₁ : M₁B = s:t.

Тогда по теореме Фалеса DN₁ : N₁C = s:t.

Проведем BT II CD. M₁N₁ = M₁L + LN₁. LN₁ = BC = TD = b, AT = AD – TD = a – b.

Из подобия треугольников  M₁BL и  АBТ :

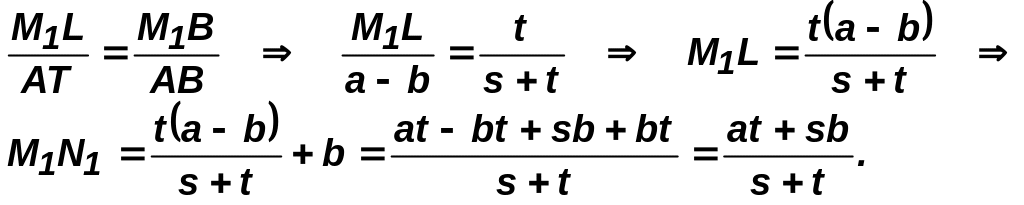
2. Отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей.

Из подобия треугольников  ВОС и  АOD :

3. Отрезок, параллельный основаниям трапеции и делящий ее на две подобные трапеции.

Из подобия трапеций AM₁N₁D и M₁BCN₁:

В математике числа 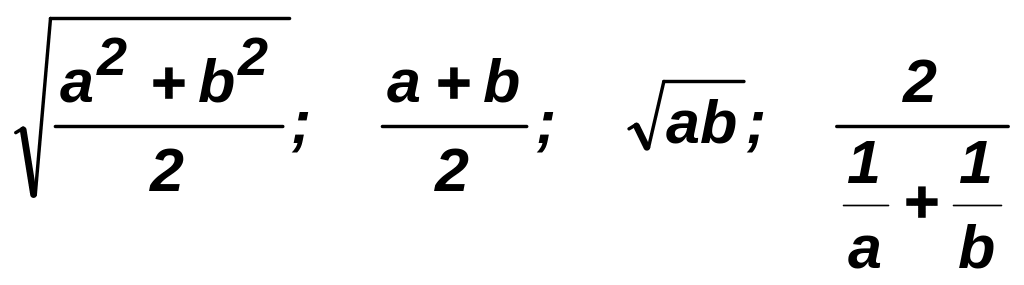называются соответственно средним квадратичным, средним арифметическим, средним геометрическим (средним пропорциональным) и средним гармоническим чисел a и b. Для положительных чисел a и b справедливы неравенства:

причем равенство достигается при a = b.

Выводы:

1. Прямая, параллельная основаниям трапеции и проходящая через точку пересечения диагоналей, является средним гармоническим оснований, ее длина равна

2. Прямая, параллельная основаниям трапеции и делящая ее на две подобные трапеции, является средним геометрическим оснований, ее длина равна

3. Средняя линия трапеции является средним арифметическим оснований.

4. Прямая, параллельная основаниям трапеции и делящая ее на две равновеликие трапеции, является средним квадратичным оснований, ее длина равна

Д оказательство:

По принципу равновеликости:

Используя полученные формулы, составим и решим уравнение:

T

№ 1 (10.034).

Из одной точки проведены две касательные к окружности. Длина каждой касательной 12 см, а расстояние между точками касания 14,4 см. Определите радиус окружности.

№ 2 (10.060).

Радиусы вписанной и описанной окружностей прямоугольного треугольника равны соответственно 2 и 5 см. Найти катеты треугольника.

№ 3 (10.111).

Сторона правильного треугольника, вписанного в окружность, равна а. Вычислить площадь квадрата, вписанного в ту же окружность.

№ 4 (10.135).

Основание треугольника равно 30 см, а боковые стороны равны 26 и 28 см. Высота разделена в отношении 2:3 (считая от вершины), и через точку деления проведена прямая, параллельная основанию. Определить площадь полученной при этом трапеции.

№ 5 (10.062).

В большем из двух концентрических кругов проведена хорда, равная 32 см и касающаяся меньшего круга. Определить длину радиуса каждого из кругов, если ширина образовавшегося кольца равна 8 см.

№ 6 (10.160).

В трапеции, площадь которой равна 594 м², высота 22 м, а разность параллельных сторон равна 6 м, найти длину каждой из параллельных сторон.

№ 7 (10.036).

В прямоугольный треугольник с углом 60 вписан ромб со стороной, равной 6 см, так, что угол в 60 у них общий и все вершины ромба лежат на сторонах треугольника. Найти стороны треугольника.

№ 7 (10.145).

Высота ромба равна 12 см, а одна из его диагоналей равна 15 см. Найти площадь ромба.

№ 8 (10.144).

В прямоугольнике проведены биссектрисы двух углов, прилежащих к большей стороне. На какие части делится площадь прямоугольника этими биссектрисами, если стороны прямоугольника равны 2 и 4 м?

№ 9 (10.121).

Вычислить площадь прямоугольной трапеции, если ее острый угол равен 60, меньшее основание равно а, а большая боковая сторона равна b.

№ 10 (10.188).

Радиус окружности, описанной около прямоугольного треугольника, относится к радиусу вписанной в него окружности как 5:2. Найти площадь треугольника, если один из его катетов равен а.

№ 11 (10.136).

В прямоугольном треугольнике биссектриса острого угла делит противоположный катет на отрезки длиной 4 и 5 см. Определить площадь треугольника.

№ 12 (10.203).

Из одной точки окружности проведены две хорды длиной 9 и 17 см. Найти радиус окружности, если расстояние между серединами данных хорд равно 5 см.

№ 13 (10.097).

Площадь прямоугольного треугольника равна Определить его высоту, проведенную к гипотенузе, если она делит прямой угол в отношении 1:2.

№ 14 (10.134).

В равнобедренной трапеции одно основание равно 40 см, а другое равно 24 см. Диагонали трапеции взаимно перпендикулярны. Найти ее площадь.

№ 15 (10.053).

В параллелограмме ABCD высота, проведенная из вершины В тупого угла к стороне AD, делит ее в отношении 5:3, считая от вершины D. Найти отношение AC:BD, если AD:AB = 2.

№ 16 (10.005).

В прямоугольный треугольник с катетами а и b вписан квадрат, имеющий с треугольником общий прямой угол. Найти периметр квадрата.

№ 17 (10.031).

В ромб, который делится своей диагональю на два равносторонних треугольника, вписана окружность радиуса 2. Найти сторону ромба.

№ 18 (10.273).

Высота, проведенная к гипотенузе прямоугольного треугольника, делит его на два треугольника с площадями Q и q. Найти катеты.

№ 19 (10.141).

Определить боковые стороны равнобедренной трапеции, если ее основания равны 8 и 14 см, а площадь равна 44 см².

№ 20 (10.061).

Перпендикуляр, проведенный из вершины параллелограмма к его диагонали, делит эту диагональ на отрезки длиной 6 и 15 см. Разность длин сторон параллелограмма равна 7 см. Найти длины сторон параллелограмма и его диагоналей.

№ 21 (10.090).

Расстояние от центра круга до хорды длиной 16 см равно 15 см. Найти площадь треугольника, описанного около круга, если периметр треугольника равен 200 см.

№ 22 (10.187).

Высота, проведенная к основанию равнобедренного треугольника, равна Н и вдвое больше своей проекции на боковую сторону. Найти площадь треугольника.

№ 23 (10.131).

В ромб с острым углом 30 вписан круг, площадь которого равна Q. Найти площадь ромба.

№ 24 (10.067).

Внутри круга радиуса 15 см взята точка М на расстоянии 13 см от центра. Через эту точку проведена хорда длиной 18 см. Найти длины отрезков, на которые точка М делит хорду.

№ 25 (10.162).

Вычислить площадь равнобедренного треугольника, если длина высоты, проведенной к боковой стороне, равна 12 см, а длина основания равна 15 см.

№ 26 (10.164).

Вычислить площадь трапеции ABCD (AD II BC), если длины ее оснований относятся как 5:3 и площадь треугольника ADM равна 50 см², где М – точка пересечения прямых АВ и СD.

№ 27 (10.057).

Диагональ прямоугольной трапеции и ее боковая сторона равны. Найти длину средней линии, если высота трапеции равна 2 см, а боковая сторона равна 4 см.

№ 28 (10.084).

Периметр ромба равен 2 м, длины его диагоналей относятся как 3:4. Найти площадь ромба.

№ 29 (10.020).

В пересечение двух равных кругов вписан ромб с диагоналями 12 и 6 см. Найти радиус окружностей.

№ 30 (10.129).

В равнобедренную трапецию вписан круг. Одна из боковых сторон делится точкой касания на отрезки длиной m и n. Определить площадь трапеции.

№ 31 (10.253).

Для треугольника со сторонами 26, 28 и 30 см найти произведение радиусов вписанной и описанной окружностей.

№ 32 (10.104).

Периметр прямоугольного треугольника равен 24 см, площадь его равна 24 см². Найти площадь описанного круга.

№ 33 (10.161).

Через вершину метр прямого угла прямоугольного треугольника с катетами 6 и 8 м проведен перпендикуляр к гипотенузе. Найти площади образовавшихся треугольников.

№ 34 (10.184).

Вычислить площадь трапеции, параллельные стороны которой содержат 16 и 44 см, а непараллельные – 17 и 25 см.

№ 35 (10.059).

В окружности радиуса r проведена хорда, равная 0,5r. Через один конец хорды проведена касательная к окружности, а через другой – секущая, параллельная касательной. Найти расстояние между касательной и секущей.

№ 36 (10.140).

Доказать, что если через вершины четырехугольника провести прямые, параллельные его диагоналям, то площадь параллелограмма, определяемого этими прямыми, в 2 раза больше площади данного четырехугольника.

№ 37 (10.040).

В прямоугольный треугольник вписана полуокружность так, что диаметр лежит на гипотенузе, а центр делит гипотенузу на отрезки длиной 15 и 20 см. Найти площадь треугольника и длину вписанной полуокружности.

№ 38 (10.166).

Один из катетов прямоугольного треугольника равен 15 см, а радиус окружности, вписанной в треугольник, равен 3 см. Найти площадь треугольника.

№ 39 (10.049).

Точка на гипотенузе, равноудаленная от обоих катетов, делит гипотенузу на отрезки длиной 30 и 40 см. Найти катеты треугольника.

№ 40 (10.163).

Стороны треугольника равны 13, 14 и 15 см. Найти отношение площадей описанного и вписанного в треугольник кругов.

№ 41 (10.004).

Высота ромба, проведенная из вершины тупого угла, делит его сторону на отрезки длиной m и n, считая от вершины острого угла. Определить диагонали ромба.

№ 42 (10.099).

Площадь равнобедренной трапеции, описанной около круга, равна 8 см². Определить стороны трапеции, если угол при основании содержит 30.

№ 43 (10.214).

Около круга радиуса 3 описан равнобедренный треугольник с острым углом 30 при основании. Определить стороны треугольника.

№ 44 (10.204).

Из одной точки окружности проведены две хорды длиной 10 и 12 см. Найти радиус окружности, если расстояние от середины меньшей хорды до большей хорды равно 4 см.

№ 45 (10.174).

Площадь равнобедренной трапеции, описанной около круга, равна S. Определить радиус круга, если угол при основании трапеции равен 30.