ДЕ17. СЛОЖНОЕ СОПРОТИВЛЕНИЕ
7.1. Виды нагружения стержня
Задание № 7.1.1.
Любая комбинация простых деформаций стержня называется…
Варианты ответа:
1. Деформированным состоянием в точке
Ответ неверный! Совокупность линейных и угловых деформаций по различным направлениям и плоскостям в одной точке называют деформированным состоянием в точке.
2. Напряженным состоянием в точке
Ответ неверный! Совокупность напряжений для множества площадок, проходящих через точку, образует напряженное состояние в точке.
3. Косым изгибом
Ответ неверный! Под косым изгибом понимается такой случай изгиба, при котором плоскость изгибающего момента не совпадает с главной осью сечения.
4. Сложным сопротивлением
Ответ верный! На практике элементы конструкций подвергаются действию сил, вызывающих одновременно несколько простых деформаций. Валы машин подвергаются деформациям кручения и изгиба. Элементы различных систем испытывают изгиб и растяжение (сжатие). Все случаи, когда в стержне возникают комбинации простых деформаций, называются сложным сопротивлением. Напряженным состоянием в точке
З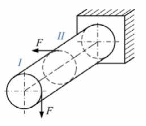
адание
№ 7.1.2.
Определите виды нагружения участков стержня.
1. I – плоский изгиб с кручением II – косой изгиб
Ответ неверный! Если главный вектор внешних сил пересекает ось стержня круглого поперечного сечения, то косой изгиб не возникает.
2. I и II – плоский изгиб
Ответ неверный! Сила, создающая момент относительно оси стержня, вызывает его кручение.
3. I и II – плоский изгиб с кручением
Ответ неверный! Сила, создающая момент относительно оси стержня, вызывает его кручение.
4. I – изгиб с кручением II – плоский изгиб
О
твет
верный:
Поперечные силы условно не показаны
П
оэтому
косой изгиб на участке II
можно свести
к плоскому изгибу моментом
На
участке I
сила 
вызывает
деформацию – плоский изгиб с кручением.
На
участке II
– плоский изгиб.
Задание № 7.1.3.
Укажите вид нагружения стержня, при котором напряженное состояние в опасных точках можно считать линейным:
а) внецентренное растяжение-сжатие; б) косой изгиб; в) изгиб с кручением; г) косой изгиб с сжатием.
Варианты ответа:
1. Только в
Ответ неверный! Вспомните, какие напряжения возникают в поперечных сечениях стержня при изгибе и при кручении.
2. Только а
Ответ неверный! Как при чистом изгибе, так и при растяжении-сжатии, точки стержня находятся в линейном напряженном состоянии.
3. Во всех случаях
Ответ неверный! Рассмотрите элементарный параллелепипед, вырезанный в окрестности опасной точки, с действующими на его гранях напряжениями.
4. Только а, б, г
Ответ верный! При этом не учитывают, как правило, касательные напряжения от поперечных сил.
Задание №7.1.4.
При внецентренном растяжении (сжатии) стержня в поперечном сечении возникают …
1. Поперечная сила и изгибающий момент
Ответ верный! Допущена ошибка при определении внутренних силовых факторов, которые возникают при внецентренном растяжении (сжатии) стержня. Данные внутренние силовые факторы возникают в сечении стержня при поперечном изгибе стержня.
2. Крутящий и изгибающий моменты
Ответ неверный! При внецентренном растяжении (сжатии) сила расположена параллельно продольной оси стержня, следовательно, крутящий момент будет равен нулю.
3. Продольная сила и крутящий момент
Ответ неверный! При внецентренном растяжении (сжатии) в поперечном сечении стержня возникают продольная сила и изгибающий момент. Крутящий момент равен нулю.
4. Продольная сила и изгибающий момент
О
твет
верный! Стержень
нагружен двумя равными и противоположно
направленными силами F,
линия
действия которых параллельна оси
стержня. Координаты точки приложения
силы в системе главных центральных осей
и .
Рассекаем
стержень поперечным сечением на две
части. Отбросим, например, правую часть.
Из условия равновесия оставшейся левой
части следует, что в поперечном сечении
отличны от нуля два внутренних силовых
фактора: продольная сила 
и
изгибающий момент, который можно
разложить на составляющие по координатам
осям:
и
Следовательно, при внецентренном растяжении (сжатии) в поперечном сечении возникают продольная сила и изгибающий момент.
З
адание
№7.1.5.
При данном нагружении стержень прямоугольного поперечного сечения испытывает…
1. Плоский поперечный изгиб
Ответ неверный! Ответ неполный. Стержень также испытывает деформацию кручения.
2. Кручение
Ответ неверный! Ответ неполный. Наряду с кручением стержень работает на плоский поперечный изгиб.
3. Кручение и изгиб
Ответ неверный! Ответ некорректный. Есть понятия «чистый изгиб» и «поперечный изгиб». В данном случае нагружения стержня в поперечном сечении возникает поперечная сила. Поэтому стержень испытывает кручение и плоский поперечный изгиб.
4. Кручение и плоский поперечный изгиб
О
твет
верный! Используя
метод сечений, рассекаем стержень
произвольным сечением на две части.
Отбросим
часть стержня, где расположена заделка.
Из условия равновесия оставшейся части
следует, что в поперечном сечении отличны
от нуля три внутренних силовых фактора:
крутящий момент ,
поперечная сила ,
изгибающий момент .
Следовательно, стержень испытывает кручение и плоский поперечный изгиб.
Задание №7.1.6.
Для вывода формул сложного сопротивления используется …
Варианты ответа:
1. Гипотеза о сплошности и однородности материала
Ответ неверный! Для вывода формул сложного сопротивления используется принцип независимости действия сил, который не связан с упомянутой гипотезой.
2. Принцип Сен-Венана
Ответ неверный! Принцип Сен-Венана гласит: в сечениях, достаточно удаленных от мест приложения нагрузки, величина напряжений весьма мало зависит от способа нагружения при условии статической эквивалентности способов нагружения.
3. Гипотеза о линейной зависимости между деформациями и нагрузками (закон Гука)
Ответ неверный! Для вывода формул сложного сопротивления используется принцип независимости действия сил, который не связан с законом Гука.
4. Принцип независимости действия сил
Ответ верный! Для вывода формул сложного сопротивления используется принцип независимости действия сил: результат действия на тело системы сил равен сумме результатов действий каждой силы в отдельности.