Проверка адекватности модели

Так как планы, используемые в методе симплексных решеток, являются полностью насыщенными (число опытов равно числу определяемых коэффициентов уравнения), то для проверки адекватности (соответствия реальной ситуации) не остается степеней свободы. В связи с этим для проверки адекватности ставятся опыты в контрольных точках. Количество точек и их расположение зависят от интересующей исследователя области диаграммы, постановки задачи, сложности опытов, экономических соображений и т.д. Общие рекомендации по выбору контрольных точек сводятся к следующему: во-первых, к необходимости изучения области симплекса представляющей наибольший интерес для исследователя, а во-вторых, к возможности использования данных контрольных опытов (или части из них) для перехода к модели более высокой степени. Например, при построении модели неполной третьей степени в тройной системе необходимо определить свойства у семи составов (см. рис. 1) . В этом случае целесообразно провести опыты еще в трех точках, соответствующих составам: х₁₁₂₃, х₁₂₂₃, х_1233. Для модели неполной третьей степени они будут проверочными, в случае неадекватности этой модели три указанные точки помогут перейти к модели неполной четвертой степени, а уже точка х₁₂₃ станет проверочной.

Адекватность модели проверяется расчетом для контрольных точек значений статистического критерия Стьюдента (Приложение 1) по формуле:

(14),

где y = y_эксп – y_расч  – абсолютная величина разности между экспериментально определенным и рассчитанным по модели значением свойства в контрольной точке; – среднеквадратичная ошибка опыта;  – уровень значимости (обычно  = 0,05), вероятностная величина, показывающая, каков риск ошибиться в правильности гипотезы и связана с Р – доверительной вероятностью, величиной определяющей степень вероятности принимаемой гипотезы ( = 1 – Р); f – число степеней свободы при определении дисперсии опыта f=N( r–1); N – число составов при определении дисперсии опыта.

Полученная модель признается адекватной в случае t_эксп  t_табл. Величина t_табл берется из таблицы значений критерия Стьюдента для данного уровня значимости() и числа степеней свободы (f).

Менее строго можно сделать вывод об адекватности модели в случае, когда величина y_эксп – y_расч  сравнима со среднеквадратичной погрешностью опыта.

Исследование локальных концентрационных участков системы

Во многих случаях для исследования представляет интерес не вся область концентраций компонентов, а только ее часть. Для применения метода симплексного планирования необходимо, чтобы локальный участок представлял бы собой симплекс (треугольник, тетраэдр и т.д.) подобный исходному с вершинами Z₁, Z₂, Z₃. Если локальный участок представлен другой фигурой, например, четырехугольником, то это может существенно затруднить расчеты. Для системы с псевдокомпонентами также справедливо условие нормировки.

Исследование локального участка, например, может иметь место при исследовании свойств фарфоровых масс, где за исходные компоненты принимаются составляющие шихты: глина (каолин), полевой шпат и кварц. Поскольку получить фарфор, используя любой из компонентов в чистом виде невозможно, то исследуется локальная область на основе псевдокомпонентов Z₁ (состоящего из 20% полевого шпата, 30% кварца и 50% глины), Z₂ (состоящего из 30% полевого шпата, 20% кварца и 50% глины) и Z₃ (состоящего из 30% полевого шпата, 30% кварца и 40% глины). Составление матрицы планирования в этом случае сводится сначала к определению опытных составов в псевдокомпонентах, а потом к пересчету на исходные компоненты.

Для удобства расчетов имеет смысл в полученных уравнениях перейти от псевдокомпонентов к исходным компонентам Х₁, Х₂, Х₃. Целесообразно также представить результаты графически в виде проекций линий равных значений физико-механических свойств на симплекс. Полученные зависимости позволяют определить точку (область), соответствующую составу, который характеризуется экстремальным значением оптимизируемого свойства. Может получиться так, что исследуемая зависимость не носит экстремальный характер, как это представлено на диаграмме состав–свойство (рисунок 2) для характеристики прочности и теплопроводности керамического (глиняного) кирпича при разном составе шихты. Но и в данном случае определение зависимости состав–свойство имеет большое практическое значение, так как позволяет выбрать состав для производства кирпича с допустимым значением прочности, но повышенной теплопроводностью.

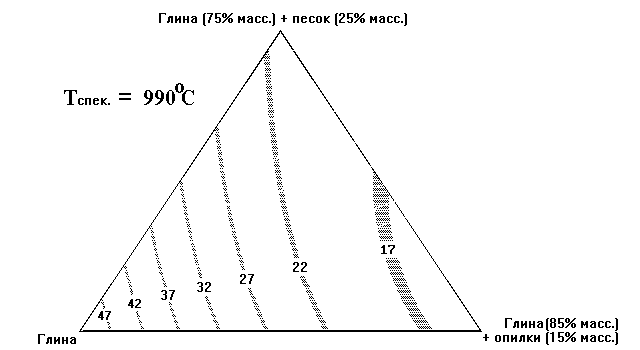
Рисунок 2 – Проекция линий равных значений прочности при изгибе на концентрационный треугольник (симплекс)