§ 3. Ряды Тейлора
1˚. Вещественные степенные ряды
Степенной ряд будем называть вещественным степенным ря- дом, если все его коэффициенты сk и центр круга сходимости а являются вещественными числами. Ряды, рассмотренные в примерах 17,18, и 19 ,§ 1, - это вещественные степенные ряды.
Опишем поведение вещественного степенного ряда . в точках вещественной оси Пусть R – радиус сходимости этого ряда. Интервал (а–R; а+R) является диаметром круга сходимости; поэтому в каждой точке этого интервала ряд абсолютно сходится; Точки вещественной оси, лежащие вне сегмента [а–R; а+R], находятся вне окружности | z- a | = R, ограничивающей круг сходимости; поэтому ряд в таких точках расходится. Что касается точек а ± R , то есть ряды, сходящиеся в каждой из них, есть ряды расходящиеся в обеих этих точках, наконец, есть и такие, которые в одной из них сходятся, а в другой расходятся ( пример 19, § 1).
Пусть заданы последовательность вещественных чисел и веществен- ное число а. Рассмотрим функциональный ряд (х), где при любом ве -щественном х и любом натуральном k fk(x) = ck-1(x-a) . Обозначим через Х0 , Х0 R , множество сходимости этого ряда, а через S(x) – его сумму. Оче- видно, ряд (х) - это вещественный степенной ряд :
(1)
Из сказанного выше явствует, что множество сходимости Х0 ряда (1) пред- ставляет собой или интервал (а–R; а+R), где R – радиус сходимости, или сег- мент [а–R; а+R], или один из полуоткрытых промежутков, ограниченных точками а ± R . Интервал (а–R; а+R) называют интервалом сходимости ряда (1). В его точках сходимость ряда всегда абсолютная. Выясним вопрос о рав- номерной сходимости ряда (1).
Теорема 1. ( О равномерной сходимости степенногоь ряда внутри интер- вала сходимости) Пусть радиус сходимости R ряда (1) больше нуля (слу- чай R=+∞ не исключен). Ряд (1) равномерно сходится на всяком сегменте, со- держащемся в интервале сходимости (а–R; а+R).
► Для
доказательства теоремы достаточно
установить равномерную схо-
димость
ряда на всяком сегменте вида [а–r;
а+r], где
0<r<R, ибо для любого сегмента [α
; β],
содержащегося в интервале (а–R;
а+R) всегда
можно подоб-
рать r,
0<r<R, такое, что [α
; β]
[а–r;
а+r], и если
ряд равномерно сходится на [а–r;
а+r], то он
равномерно сходится и на [α
; β].
Итак,
пусть задано некоторое r, 0<r<R..
Обозначим: через х0
любую
из то-
чек а±
r. Так как х0
(а–R;
а+R) , ряд (1)
абсолютно сходится в этой точке, т.е.
сходится ряд
;
кроме того, для всякого х
[а–r;
а+r] имеем :
при
всех k = 0,1, … Отсюда и из признака
Вейерштрасса (теорема 3, § 2) вытекает
равномерная сходимости (1) на сегменте
[а–r;
а+r]. ◄
Замечание 1. Хотя ряд равномерно сходится на всяком сегменте, содержащемся в (а–R; а+R), он не всегда является равномерно сходящимся на всем этом интервале.
Замечание 2. Если ряд сходится в точке а+R, он равномерно сходится на всяком сегменте [а–r; а+R] , где0<r<R.. Если ряд сходится в точке а–R, он равномерно сходится на всяком сегменте [а–R; а+r],где 0<r<R. Доказатель- ства этих утверждений можно найти в [1], том 1.
Последующие теоремы посвящены свойствам суммы вещественного степенного ряда.
Теорема 2. (О непрерывности суммы степенного ряда ) Сумма S степен- ного ряда (1) непрерывна на интервале сходимости этого ряда.
► Пусть х0 – некоторая точка интервала сходимости (а–R; а+R). Подберем r, 0<r<R, такое, чтобы было выполнено х0 [а–r; а+r] По теореме 1 ряд равномерно сходится на [а–r; а+r] . Так как члены ряда непрерывны на [а–r; а+r], в силу теоремы 5, § 2, его сумма S также непрерывна на [а–r; а+r]. Значит, S непрерывна в точке х0. Так как х0 - любая точка интервала (а–R; а+R), доказана непрерывность S на этом интервале. ◄
Замечание. Из замечания 2 к теореме 1 и теоремы 4, § 2 вытекает: если ряд (1) сходится в точке а+R, то S непрерывна на промежутке (а–R; а+R] ; если ряд (1) сходится в точке а-R, то S непрерывна на промежутке [а–R; а+R) .
Пусть
х – некоторое вещественное число.
Заметим: при любом k = 0,1, . …
.
Мы будем говорить, что ряд
(2)
получен почленным интегрированием ряда (1). Ряд (2) представляет собой также вещественный степенной ряд. Его радиус сходимости обозначим через Ri , его сумму – через Si .
Теорема
3.
(О
почленном интегрировании степенного
ряда )
1) Радиус
сходимости
ряда (2) не меньше рядиуса сходимости
ряда (1).
2) Для
любого х
(а–R;
а+R) Si(х)
=
,
где S – сумма ряда (1).
► Выберем некоторое х (а–R; а+R). По теореме 1 ряд (1) равномерно сходится на сегменте, ограниченном точками а и х; значит, в силу теоремы 5. § 2, ряд (1) можно почленно проинтегрировать по указанному сегменту:
,
т.е.
= Si(х).
Мы доказали тем самым, что ряд (2) сходится в точке х и нашли значение его суммы в этой точке. Но х – произвольная точка интервала (а–R; а+R). Значит, (2) сходится в каждой точке этого интервала и поэтому утверждение 1) теоремы справедливо. Утверждение 2) теоремы. также доказано. ◄
Мы будем говорить, что ряд
(3)
получен почленным дифференцированием ряда (1). Ряд (3) есть веществен- ный степенной ряд. Его радиус сходимости обозначим через Rd, его сумму – через Sd.
Теорема 4. ( О почленном дифференцировании степенного ряда ) 1) Радиус сходимости ряда (3) не меньше радиуса сходимолсти ряда (1) . 2) Сумма S(x) ряда (1) дифференцируема в каждой точке интерала сходимо- сти (а–R; а+R), причем на этом интервале S′(x) = Sd(x).
► 1)
Выберем некоторое х
(а–R;
а+R) и
докажем,что (3) сходится в этой точке.
Найдется r, 0<r<R, такое, что х
[а–r;
а+r]. Так как
х0
= а+r
при-
надлежит
(а–R;
а+R) , ряд (1)
абсолютно сходится в этой точке,т.е.
сходится ряд
.
Общий член этого ряда стремится к нулю,
значит, последова-
тельность
{|ck|
|}
ограничена: существует М > 0 такое,
что при всех k |ck|
|
≤ M. Теперь для выбранного выше х
получим:
,
где
q =
< 1. С помощью признака Даламбера
нетрудно установить, что ряд
сходится;. Значит, сходится
и ряд
,
т.е. (3) абсо-
лютно
сходится в выбранной точке х.
Но х
– произвольная точка интервала (а–R;
а+R),
следовательно (3) сходится на этом
интервале и поэтому Rd
≥ R. .
2)
Почленно
проинтегрируем
ряд (3): так как
, то получим
ряд
.
Очевидно, его сумма равна S(x) – с0.
По теореме З S(x) – с0=
.
Отсюда: S(x) = с0
+
.
Sd –
непрерывная функция как сумма степенного
ряда, поэтому интеграл с переменным
верхним пределом
- функция, дифференцируемая, причем ее
производная равна Sd.
Значит, если
х
(а–R;
а+R) ,
то S′(x)
= Sd(x).
◄
Следствие. Сумма степенного ряда имеет на интервале сходимости производные любого порядка.
► Действительно, Сумма S(x) ряда (1) – дифференцируемая функция, производная которой S′ (x) есть сумма ряда (3), полученного почленным дифференцированием ряда (1). Таким образом, S′ (x) в свою очередь явля- ется суммой степенного ряда (3); значит, она дифференцируема, а ее произ- водная S″(x) является суммой степенного ряда, полученного почленным диф- ференцированием ряда (3). Эти рассуждения могут быть продолжены неогра- ниченно. ◄
Теорема 5. (О сохранении радиуса сходимости при почленном интегриро- вании и дифференцировании степенного ряда ) Пусть R, Ri и Rd – радиусы сходимости рядов (1),(2) и (3) соответственно. Тогда R = Ri = Rd.
► При почленном интегрировании и дифференцировании степенного ряда радиус сходимости не уменьшается (утверждения 1) теорем 3 и 4 ). Почленно проинтегрировав ряд (3), получим ряд ( см. доказа -тельство предыдущей теоремы), радиус сходимости которого, очевидно, ра- вен R; значит, R ≥ Rd. Вместе с неравенством Rd ≥ R (теорема 4) это даст Rd= R. Аналогично, почленно дифференцируя (2), докажем равенство Ri = R. ◄
Теорема
6. (
О коэффициентах
степенного ряда
) 1) Для коэффициентов сk
ряда (1) справедливы равенства : с0
= S(а)
и при всяком натуральном k ck=
.
2)
Пусть
есть сумма некоторого
вещественного
степенного ряда
;
если на некотором интервале (а–δ;
а+δ)
, где δ > 0,
≡
S(х), то коэффициенты ряда
совпадают с соответствующими коэффици-
ентами
ряда (1) : при всех k = 0,1, …
.
► 1) При всяком х на (а–R; а+R) имеем:
S(х)
=
.
Последовательно дифференцируем это равенство:
S′(х)
=
S′′(х)
=
…………………………………………………….
S
(х) = k(k-1)…2·1ck
+ (k+1)k…2
ck+1(x-a)+
… ;
………………………………………………………
при х=а из этих равенств получаем: S(а) = с0 ; S′(а) = с1 ; S′′(а) = 2 с2 ; … S (а) = = k! ck, … , что и требовалось доказать.
2)
Так как
≡
S(х) на (а–δ;
а+δ),
то
и при всех натуральных k
.
Отсюда:
=
с0
, и при всех натуральных k
=
.
◄
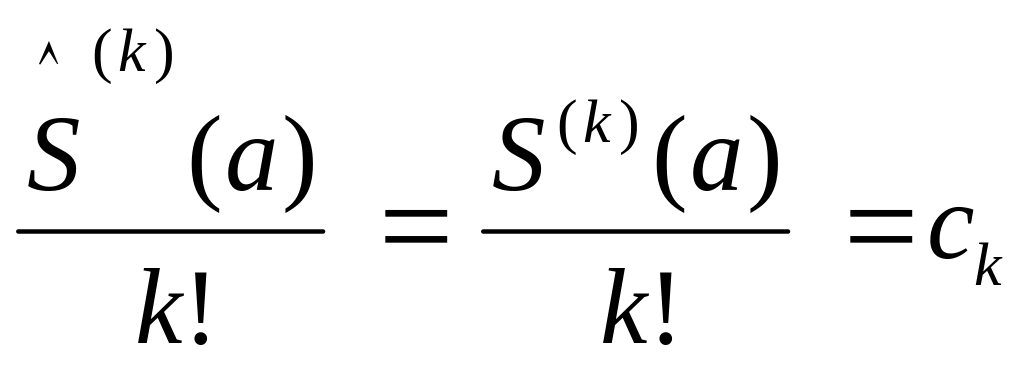