3°. Функциональные ряды

Пусть на множестве Х определена последовательность функций . Рассмотрим функциональную последовательность {S_n},где S₁ = f₁ ,a при n ≥2 S_n = f₁+ f₂ + …+ f_n . Если Х₀ – множество сходимости последовательности {S_n}, а S - ее предельная функция, то будем говорить, что функциональный ряд

f₁(х)+ f₂(х) + …+ f_n(х)+ … = (х)

сходится на множестве Х₀ , а функцию S назовем суммой этого ряда; при этом будем записывать : = S или . Члены последо- вательности называют членами ряда , а сумму S_n = - его n-ой частичной суммой. Отметим, что сумма ряда есть предельная функция после- довательности его частичных сумм: .

Пример 4. Пусть f_k(x) = x , x R. Рассмотрим ряд

Имеем:

S_n(х) =

Отсюда нетрудно увидеть, что при |x| < 1; если же |x| ≥ 1, то последовательность {S_n (х)} расходится. Следовательно, рассматриваемый ряд сходится на интервале Х₀ =(-1 ; 1), а его сумма есть S(х) .

Опираясь на известные свойства числовых рядов, нетрудно прийти к сле- дующим выводам.

1) Если ряд (х) сходится на некотором множестве Е ,то , т.е. последовательность членов ряда сходится на Е , и ее предельная функция тождественно на Е равна нулю.

2) Если функциональный ряд (х) | сходится на некотором множест- ве Е ,то и ряд (х) сходится на этом множестве.

Пусть ряд (х) | сходится на множестве Е . В этом случае будем говорить, что ряд (х) абсолютно сходится на Е.

4˚. Равномерно сходящиеся функциональные ряды

Пусть Х₀ - множество сходимости функционального ряда , а Е – некоторое множество, ( случай Е = Х₀ не исключен).

Определение. Будем говорить, что ряд равномерно сходится на множестве Е, если последовательность его частичных сумм равномерно сходится на этом множестве : .

Теорема 3. ( Признак Вейерштрасса) Пусть заданы функциональный ряд , члены которого определены на некотором множестве Е, и числовой ряд с неотрицательными членами. Если 1) при всех натуральных k и всех х, справедливы неравенства f_k(x) | ≤ a_k и 2) ряд сходится, то ряд сходится на Е абсолютно и равномерно.

► Из условия 1) теоремы и первого признака сравнения ( 3˚,§ 1) следует, что ряд (х) | сходится на множестве Е ; значит, (х) абсолютно сходится на этом множестве. Докажем, что , т.е., что

N n N x R ( (n > n_ε)

Зададим ε > 0. Так как сходится, в силу критерия сходимости Коши (2˚,§ 1) существует натуральное n_ε такое, что при всех n > n_ε и любых натуральных р выполняется . Выберем некоторое n > n_ε. При всяком натуральном р и любых х Е имеем:

.

Перейдем в неравенстве к пределу при р→ ∞ : .

Заметим: . Таким образом, для всякого ε > 0 существует n_ε такое, что при всех n > n_ε и любых х Е справедливо |S_n(x) – S(x) | < ε, что и требовалось доказать. ◄

Вообще говоря, сумма функционального ряда, члены которого непрерыв- ные (дифференцируемые ) функции, не обязательно является непрерывной (дифференцируемой ) функцией. Но для равномерно сходящихся рядов ука- занные свойства членов ряда передаются его сумме, о чем свидетельствуют следующие теоремы.

Теоерма 4. (О непрерывности суммы ряда) Пусть члены ряда (х) непрерывны на промежутке . Если ряд равномерно сходится на , то его сумма S(x) также непрерывна на этом промежутке.

► Так как члены ряда непрерывны, то любая его частичная сумма S_n(x) – непрерывная на функция. Значит, S(x) есть предельная функция равно- мерно сходящейся последовательности непрерывных функций; в силу теоре- мы 1 S(x) непрерывна на . ◄

Теорема 5. (О почленном интегрировании ряда) Пусть члены ряда (х) непрерывны на сегменте [a;b]. Если ряд равномерно сходится на [a;b], то числовой ряд сходится, причем , где S(x) – сумма ряда (х) .

► Обозначим : σ = , Ι _k = . Нужно доказать, что числовой ряд сходится, а число σ есть его сумма: σ = .

Последовательность {S_n (х)} частичных сумм – это последовательность непрерывных функций, равномерно сходящаяся на [a;b] к S(x). По теореме 2 = , а это и есть равенство σ = . ◄

Замечание. Доказанной теореме можно дать такую формулировку: если ряд сходится равномерно, то его можно почленно проинтегрировать, т.е., знак интеграла можно внести под знак бесконечной суммы:

.

Теорема 6. ( О почленном дифференцировании ряда) Пусть члены ряда (х) непрерывно дифференцируемы на сегменте [a;b]. Если 1) ряд (х) сходится на [a;b] и 2) ряд сходится на [a;b] равномерно, то сумма S(x) ряда (х) также дифференцируема на [a;b], а ее производ- ная S’(x) есть сумма ряда .

► Обозначим сумму ряда через σ(х). Пусть ξ – некоторая точка промежутка (a;b]. Рассмотрим сегмент [a;ξ ] . На этом сегменте ряд удовлетворяет всем требованиям теоремы 5; значит, этот ряд можно поч- ленно проинтегрировать по сегменту [a;ξ ] : . Так как ряды (ξ) и (а) сходятся, то = (ξ)+ (а), (свойство 5, 2˚, § 1). Отсюда : = (ξ) + (а) = S(ξ) + S(a) и S(ξ) = - S(a). Последнее равенство справедливо при любом ξ [a;b]. Рассматривая интег- рал как интеграл с переменным верхним пределом от непрерывной на [a;b] функции σ(х), и опираясь на теорему о дифференцируемости интег- рала с переменным верхним пределом ( [5], п. 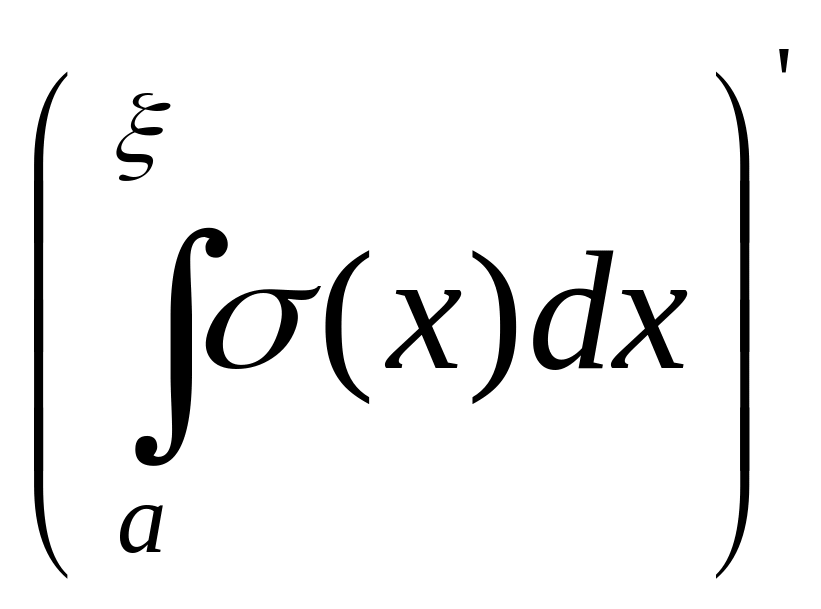1.12 ) заключаем, что есть дифференцируемая функция от ξ , причем для всякого ξ [a;b] = σ(ξ). Теперь из равества S(ξ) = - S(a) следует: функция S дифференцируема на [a;b], а ее производная есть функция σ. ◄

Замечание. Таким образом, если выполнены условия теоремы 6, то функциональный ряд (х) можно почленно продифференцировать, т.е. внести знак дифференцирования под знак бесконечной суммы :