
- •§ 1. Числовые ряды.
- •1º. Основные понятия.
- •2˚. Общие свойства числовых рядов
- •3º. Признаки сходимости рядов с неотрицательными членами.
- •4°. Признаки сходимости произвольных рядов
- •5 ˚. Абсолютно сходящиеся ряды
- •6˚. Степенные ряды.
- •§ 2. Функциональные последовательности и ряды
- •1˚. Последовательности функций
- •2˚. Равномерно сходящиеся последовательности функций
- •3°. Функциональные ряды
- •4˚. Равномерно сходящиеся функциональные ряды
- •§ 3. Ряды Тейлора
- •1˚. Вещественные степенные ряды
- •2°. Коэффициенты Тейлора. Ряд Тейлора.
- •§ 1. Числовые ряды
- •§ 2. Функциональные последовательности и ряды
- •§ 3. Ряды Тейлора
5 ˚. Абсолютно сходящиеся ряды
Если сходится ряд , то ряд также сходится ( теорема 8 ). Если же расходится, то может оказаться как сходящимся, так и расхо- дящимся рядом. Ряд называют абсолютно сходящимся рядом, если сходится . Если сходится, а расходится, то говорят, что сходится неабсолютно или условно.
Пример
13. При λ ≤ 0 ряд
![]() расходится, а при λ > 0 он
сходится ( пример 10) . Заметим:
расходится, а при λ > 0 он
сходится ( пример 10) . Заметим:
![]() ,
а
,
а
![]() расходится при 0 < λ ≤ 1 и сходится
при λ > 1. Значит, при 0
< λ ≤ 1 ряд
сходится условно, а при λ >
1 его сходимость абсолютная.
расходится при 0 < λ ≤ 1 и сходится
при λ > 1. Значит, при 0
< λ ≤ 1 ряд
сходится условно, а при λ >
1 его сходимость абсолютная.
Пример 14. Пусть φ . Ряд сходится при λ > 0 ( при- меры 11 и 12). Так как , то при 0 < λ ≤ 1 сходимость этого ряда условная, а при λ > 1 - абсолютная.
Абсолютно сходящиеся ряды представляют особый интерес, ибо они обладают свойствами, сближающими их с конечными суммами. Ниже эти свойства будут рассмотрены подробно; а пока отметим, что их наличие упрощает обращение с абсолютно сходящимися рядами; поэтому, имея дело со сходящимся рядом , важно выяснить, является ли он абсолютно схо- дящимся, для чего нужно исследовать сходимость ряда . Так как члены его неотрицательны, применимы теоремы, изложенные в 3˚. Кроме того, если z k- мнимые числа, часто оказывается полезной следующая теорема.
Теорема
11 . Пусть
и
-
последовательности вещественных чисел
. Обозначим : zk
= xk
+ i yk.
Для того чтобы ряд
абсолютно сходился, необходимо и
достаточно, чтобы абсолютно сходились
оба ряда
![]() и
и
![]() .
.
►
Необходимость. Так
как |x k|
≤ |z k|,
то в силу первого признака сравнения
из сходимости
вытекает сходимость
![]() .
Доказательство схо- димости
.
Доказательство схо- димости
![]() аналогично.
аналогично.
Достаточность. Пусть
и
сходятся; тогда сходится и
![]() .
Из неравенства |z k|
≤ |x k|
+ |yk|
и первого признака сравне- ния вытекает
сходимость
.
◄
.
Из неравенства |z k|
≤ |x k|
+ |yk|
и первого признака сравне- ния вытекает
сходимость
.
◄
Пример
15. Рассмотрим ряды
![]() и
и
![]() , где φ и λ
– вещественные числа, причем число
φ не кратно π.
Заметим:
, где φ и λ
– вещественные числа, причем число
φ не кратно π.
Заметим:
![]()
![]() ,
,
![]()
![]() .
При λ > 0 ряд
сходится; значит (свойство
71),
2˚), при λ > 0 рассматриваемые
ряды сходятся. Из примера 14 и теоремы
10 вытекает, что при λ >
1 их сходимость абсолютная, а при
0 < λ ≤ 1 сходимость хотя бы одного
из них должна быть условной.
.
При λ > 0 ряд
сходится; значит (свойство
71),
2˚), при λ > 0 рассматриваемые
ряды сходятся. Из примера 14 и теоремы
10 вытекает, что при λ >
1 их сходимость абсолютная, а при
0 < λ ≤ 1 сходимость хотя бы одного
из них должна быть условной.
Покажем,
что при 0 < λ ≤ 1 ряд
сходится условно, т.е. что при
указанных λ
![]() расходится. Сначала покажем, что
расходится ряд
расходится. Сначала покажем, что
расходится ряд
![]() .
Действительно,
.
Действительно,
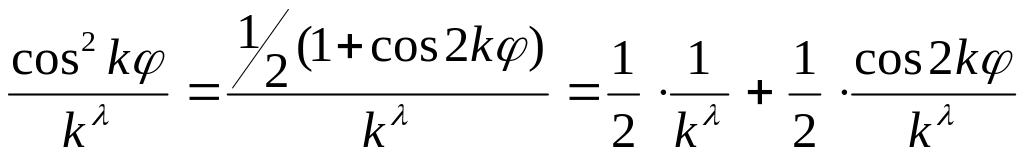 .
При 0 < λ ≤ 1 ряд
.
При 0 < λ ≤ 1 ряд
![]() расходится, а
расходится, а
![]() сходится ( см. выше). Следова- тельно
(свойство 4 и свойство 52),
2˚ ), ряд
расходится. Так как
сходится ( см. выше). Следова- тельно
(свойство 4 и свойство 52),
2˚ ), ряд
расходится. Так как
![]() ,
то
,
то
![]() ,
поэтому
,
поэтому
![]()
![]() .
По первому признаку сравнения
расходится. Аналогично можно
установить, что при 0 < λ ≤ 1 и φ
, не кратных π , ряд
.
По первому признаку сравнения
расходится. Аналогично можно
установить, что при 0 < λ ≤ 1 и φ
, не кратных π , ряд
![]() расходится.
расходится.
Итак, пусть φ - вещественное число, не кратное π. При λ > 0 ряды и сходятся, причем для 0 < λ ≤ 1 их сходимость условная, а для λ > 1 она абсолютная
Сформулируем и докажем основные свойства абсолютно сходящихся рядов .
Произведение любого числа на абсолютно сходящийся ряд есть абсо-лютно сходящийся ряд. Сумма двух абсолютно сходящихся рядов есть абсолютно сходящийся ряд.
► Пусть
![]() и
и
![]() абсолютно сходятся, а λ – некоторое
число. Так
абсолютно сходятся, а λ – некоторое
число. Так
как
![]() и
и
![]() сходятся, то сходятся и
сходятся, то сходятся и
![]() и
и
![]() ( свойства 4 и 5 , 2˚). Отсюда следует, во
– первых, что произведение
( свойства 4 и 5 , 2˚). Отсюда следует, во
– первых, что произведение
![]() абсолютно сходится. Во-вторых, так как
| z′k
+ z″k|
≤ |z′k|
+ |z″k|
, сходится
абсолютно сходится. Во-вторых, так как
| z′k
+ z″k|
≤ |z′k|
+ |z″k|
, сходится
![]() , т.е. сумма
, т.е. сумма
![]() рядов
и
абсолютно сходится . ◄
рядов
и
абсолютно сходится . ◄
Пусть
заданы две последовательности
![]() и
и
![]() .
Будем говорить, что
можно получить из
перестановкой ее членов, если для
всякого натурального j
существует натуральное kj
такое ,что w j
= z k
.
Будем говорить, что
можно получить из
перестановкой ее членов, если для
всякого натурального j
существует натуральное kj
такое ,что w j
= z k![]() ,
причем последовательность чисел
,
причем последовательность чисел
![]() отличается от натурального ряда 1,2, …
лишь порядком, в котором расположены
составляющие ее натуральные числа.
отличается от натурального ряда 1,2, …
лишь порядком, в котором расположены
составляющие ее натуральные числа.
Если
можно получить из
перестановкой ее членов, то и
последовательность
можно получить из
,
переставив ее члены: для всякого
натурального k найдется
натуральное j
k такое, что z k
= wj![]() .
.
Будем говорить, что ряд
![]() получен из ряда
получен из ряда
![]() перестановкой
его членов, если последовательность
{wj}
можно получить из {zk},
переставив ее члены.
перестановкой
его членов, если последовательность
{wj}
можно получить из {zk},
переставив ее члены.
2. ( Переместительное свойство) Пусть ряд абсолютно сходится, а S - его сумма. Если ряд получен перестановкой членов ряда , то он также абсолютно сходится, причем его сумма равна также S.
► Пусть n и m - натуральные
числа. Обозначим: S![]() ,
,
![]()
![]() ,
S
,
S![]() ,S
,S![]() .
Имеем: w j
= z k
,
j = 1,2, … ,m . Обозначим через К
наибольшее из чисел k1,
k2,
…, km
. Очевидно, К ≥ m; поэто- му S
.
Имеем: w j
= z k
,
j = 1,2, … ,m . Обозначим через К
наибольшее из чисел k1,
k2,
…, km
. Очевидно, К ≥ m; поэто- му S![]() =
=
![]()
![]() ,
где А- сумма ряда
,
где А- сумма ряда
![]() .
Таким образом, последовательность {
S
.
Таким образом, последовательность {
S![]() }
частичных сумм ряда
}
частичных сумм ряда
![]() ограничена сверху числом А, значит (
теорема 1, 3˚ ), этот ряд сходится, т.е.
сходится абсолютно.
ограничена сверху числом А, значит (
теорема 1, 3˚ ), этот ряд сходится, т.е.
сходится абсолютно.
Докажем, что число S является
суммой ряда
,
т.е. , что S![]() :
:
![]() N
N
![]()
![]() N ( m
>m ε
N ( m
>m ε
![]() )
)
Зададим некоторое ε > 0. Так как S
является пределом последовательности
{S![]() },
то ([3], п. 3.2 ), найдется
натуральное n
},
то ([3], п. 3.2 ), найдется
натуральное n![]() такое, что при всех n > n
справедливо
такое, что при всех n > n
справедливо
![]() .Так как последовательность { S
.Так как последовательность { S![]() }
сходится, в силу критерия
Коши ([3], п.3.8) существует натуральное
n
такое, что при всех n > n
и любых натуральных р cправедливо
}
сходится, в силу критерия
Коши ([3], п.3.8) существует натуральное
n
такое, что при всех n > n
и любых натуральных р cправедливо
![]() Выберем некоторое
натуральное N > max{ n
,
n
}.
Заметим:
Выберем некоторое
натуральное N > max{ n
,
n
}.
Заметим:
![]() ; при любом натуральном р
; при любом натуральном р
![]() (4)
(4)
Имеем:
zk =
wj
,
k = 1,2, …, N. Обозначим:
m ε =
max{ j1,
j2, …,
jN}.
Очевидно, m ε
≥ N. Пусть m > m ε
. Рассмотрим разность
S![]() – S . Добавляя и вычитая S
– S . Добавляя и вычитая S![]() ,
получим : S
- S = (S
– S
)
+ ( S
- S). Отсюда и из (4):
,
получим : S
- S = (S
– S
)
+ ( S
- S). Отсюда и из (4):
| S
- S| ≤ | S
– S
|
+ | S
- S| <
![]() + | S
– S
|
(5)
+ | S
– S
|
(5)
Докажем, что | S
– S
|<
.
Заметим: S
– S
=
![]()
![]() Так как m > m ε
= max{ j1,j2,
…,jN},
то S
содержит все слагаемые суммы S
;
следовательно, S
– S
представляет собой
сумму
Так как m > m ε
= max{ j1,j2,
…,jN},
то S
содержит все слагаемые суммы S
;
следовательно, S
– S
представляет собой
сумму
![]() ,
из которой удаленa часть ее слагаемых,
а именно, слагаемые с номерами j1,
j2, …,
jN .
Для оставшихся m-N слагаемых введем
обозначения: W1,
W2,
…,Wm-N
: S
– S
= W1+W2+…
…+Wm-N .
Тогда | S
– S
,
из которой удаленa часть ее слагаемых,
а именно, слагаемые с номерами j1,
j2, …,
jN .
Для оставшихся m-N слагаемых введем
обозначения: W1,
W2,
…,Wm-N
: S
– S
= W1+W2+…
…+Wm-N .
Тогда | S
– S
![]() |
≤
|
≤
![]() . Каждое из чисел Wl
, l =1,2,…, m-N, является
и членом последовательности
; пусть Wl
= zk
. Каждое из чисел Wl
, l =1,2,…, m-N, является
и членом последовательности
; пусть Wl
= zk![]() , l =1,2,…,
m-N. Введем обозначение : К = = max{
k1,k2,…,km-N}.
Каждое из чисел k1,k2,…,km-N
больше N , ибо из S
удалены слагаемые суммы S
,
т.е. числа z1,
z2, …,
zN . Значит, К >
N , т.е. К = N + р, где р -
некоторое натуральное число. Ввиду
этого можем записать:
, l =1,2,…,
m-N. Введем обозначение : К = = max{
k1,k2,…,km-N}.
Каждое из чисел k1,k2,…,km-N
больше N , ибо из S
удалены слагаемые суммы S
,
т.е. числа z1,
z2, …,
zN . Значит, К >
N , т.е. К = N + р, где р -
некоторое натуральное число. Ввиду
этого можем записать:
| S
– S
|
≤
=
![]() ≤
≤
![]()
Отсюда
и из (4) следует: | S
– S
|
<
.
Подставив эту оценку в (5), можем
утверждать: при всяком m > m ε
справедливо неравенство
![]() ◄
◄
Таким образом, сумма абсолютно сходящегося ряда , как и сумма конечного количества слагаемых, не зависит от порядка , в котором производится сложение. Отметим, что условно сходящиеся ряды подобным свойством не обладают, о чем говорит следующая теорема.
Теорема 12. (Теорема
Римана ) Пусть
![]() -
условно сходящийся ряд с вещественными
членами. Каким бы ни было заданное S
– любым вещественным числом или одним
из символов + ∞ ,- ∞ , - всегда существует
ряд
-
условно сходящийся ряд с вещественными
членами. Каким бы ни было заданное S
– любым вещественным числом или одним
из символов + ∞ ,- ∞ , - всегда существует
ряд
![]() ,
полученный из
перестановкой его членов, сумма которого
равна S.
,
полученный из
перестановкой его членов, сумма которого
равна S.
Доказательство этой теоремы можно найти в [2].
Еще одно свойство абсолютно сходящихся рядов, сближающее их с конечными суммами, связано с операцией умножения ряда на ряд.. Опишем эту операцию.
Пусть заданы два ряда и Умножая каждый член первого ряда последовательно на все члены второго, получим бесконечное множество всевозможных попарных произведений, которое запишем в виде матрицы, имеющей бесконечное количество строк и бесконечное количество столбцов :
z
 1w1
z1w2
… z1wj
…
1w1
z1w2
… z1wj
…
z2w1 z2w2 … z2wj …
….……………………………. (6)
zkw1 zkw2 … zkwj …
………………………………..
Произведением
ряда
на ряд
называют ряд, составленный из всех
элементов этой матрицы, т.е. ряд вида
![]() ,
причем каждый эле- мент матрицы
встречается в последовательности
,
причем каждый эле- мент матрицы
встречается в последовательности
![]() только один раз. Чтобы построить такой
ряд, нужно каким-нибудь способом
перенумеро- вать элементы матрицы, т.е.
каждому элементу присвоить натуральный
но- мер s, причем разным элементам должны
быть присвоены обязательно раз- личные
номера. Ниже представлены два таких
способа присваивания но -меров элементам
матрицы - ″по диагоналям″ и ″по
квадратам″:
только один раз. Чтобы построить такой
ряд, нужно каким-нибудь способом
перенумеро- вать элементы матрицы, т.е.
каждому элементу присвоить натуральный
но- мер s, причем разным элементам должны
быть присвоены обязательно раз- личные
номера. Ниже представлены два таких
способа присваивания но -меров элементам
матрицы - ″по диагоналям″ и ″по
квадратам″:


 1 2 4 7 …
1 2 5 10 …
1 2 4 7 …
1 2 5 10 …
3 5 8 … 4 3 6 11 …
6 9 …. 9 8 7 12 …
10 …. 16 15 14 13 …
Конечно, возможны и другие способы. Заметим, что два ряда, построенные различными способами, отличаются один от другого лишь порядком, в кото- ром расоложены их члены, т.е. один ряд может быть получен из другого за счет перестановки его членов.
Пусть ряды и абсолютно сходятся , а S
 и
S
и
S - суммы
- суммы
этих рядов. Тогда всякий ряд , составленный из элементов матрицы (6) также абсолютно сходится,причем его сумма равна S · S .
► Пусть
n - некоторое натуральное число. Введем
обозначения : S![]() , S
, S![]() , S
, S![]() , S
, S![]() - сумма ряда
, S
- сумма ряда
, S![]() - сумма ряда
- сумма ряда
![]() . Заметим:: S
. Заметим:: S![]() ≤ S
· S
≤ S
· S![]() , так как каждое слагаемое суммы S
содержится в произведении сумм S
· S
. Очевидно, S
≤ S
,
S
≤ ≤ S
.
Следовательно, при всяком натуральном
n S
≤ S
·
S
,т.е. после- довательность частичных
сумм ряда
, так как каждое слагаемое суммы S
содержится в произведении сумм S
· S
. Очевидно, S
≤ S
,
S
≤ ≤ S
.
Следовательно, при всяком натуральном
n S
≤ S
·
S
,т.е. после- довательность частичных
сумм ряда
![]() ограничена сверху числом S
·
S
,
значит (теорема 1, 3° ), этот ряд сходится,
а
абсолютно сходится.
ограничена сверху числом S
·
S
,
значит (теорема 1, 3° ), этот ряд сходится,
а
абсолютно сходится.
Обозначим
через S сумму ряда
и докажем, что она равна произ-
ведению
сумм рядов
и
.
Обозначим:
S![]() =
=
![]() .Заметим
,
что последовательность {S
}
сходится
к S .Так
как S не зависит от способа приписывания
номеров элементам матрицы (6),
будем считать, что в ряде
эти элементы перенумерованы ″по
квадратам″. Тогда при всяком n S
.Заметим
,
что последовательность {S
}
сходится
к S .Так
как S не зависит от способа приписывания
номеров элементам матрицы (6),
будем считать, что в ряде
эти элементы перенумерованы ″по
квадратам″. Тогда при всяком n S![]() =
S
=
S![]() S
S![]() .
Значит, S
→ S
·
S
.
Но
так как вся последовательность {S
}
сходится к S
,
то и ее подпоследовательность {
S
}
имеет
тот же предел. Следовательно,
S = S
·
S
.
◄
.
Значит, S
→ S
·
S
.
Но
так как вся последовательность {S
}
сходится к S
,
то и ее подпоследовательность {
S
}
имеет
тот же предел. Следовательно,
S = S
·
S
.
◄
