Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Омский Государственный Университет Путей Сообщения

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Tmo_kursovik.doc

Скачиваний:

Добавлен:

01.05.2025

Размер:

3.14 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 63 4 5 6 > Следующая >>>

1.3 Выводы

Процессы теплообмена, при которых температурное поле изменяется не только в пространстве, но и во времени, называются нестационарными. Это и охлаждение воздуха в течение суток, и охлаждение вскипячённой воды в чайнике с течение времени и многие другие. Из указанных примеров можно выделить два основных вида процесса нестационарной теплопроводности. Первый из них, когда нагретое или охлаждённое тело стремится к тепловому равновесию, второй, когда тело претерпевает периодические температурные изменения.

Если нагревать поверхность плиты, то сначала начинают прогреваться поверхностные слои, затем уже тепло начинает поступать в глубинные слои. Тепло от пара к стенке передаётся конвекцией, которая характеризуется интенсивностью теплообмена.

Графики показывают:

1)Увеличение скорости пара ведёт к росту коэффициента теплоотдачи. Причём зависимость прямопропорциональная. Однако по мере увеличения температуры пара влияние скорости снижается.

2) Зависимость времени нагрева от скорости потока пара – экспоненциальная, и с увеличением скорости потока время нагрева резко снижается; при увеличении температуры пара время также уменьшается вплоть до нуля при определенном значении скорости потока.

3) Количество же тепла, необходимое для нагревания поверхности плиты до температуры пара, снижается при увеличении скорости пара. При повышении температуры пара количество необходимого для нагрева поверхности плиты также уменьшается. Этот факт можно объяснить тем, что поток движущегося вдоль поверхности плиты пара конвекцией передаёт тепло поверхностному слою плиты. От поверхности плиты в глубь тепло распространяется теплопроводностью, которая не зависит от скорости и температуры пара. Нагрев поверхности плиты под воздействием пара происходит быстро. За это время поверхностный слой не успевает отдать тепло другим слоям, а при этом получает новые «порции» тепла. Тепло накапливается и, так как нет возможности быстро его передать, поверхность плиты начинает перегреваться. Этот эффект называют тепловым ударом. Так как разность между температурой поверхности плиты и глубинными слоями велика, то такой режим течения пара может привести к возникновению трещин и разрушению плиты.

2. Передача теплоты через оребренную стенку цилиндрической формы.

З а д а н и е. Исследовать эффективность оребрения поверхности цилиндрической стенки наружным диаметром 2r₁в зависимости от высоты ребра h, а также условий омывания внешней оребренной поверхности воздушным потоком со скоростью w. Температура у основания ребра t₀=120⁰С, средняя температура потока воздуха t_в=10⁰С.

Оребрение выполнено цилиндрическими ребрами прямоугольного сечения толщиной δ. Данные к заданию приведены в таблице 2.1.

Т а б л и ц а 2.1

Исходные данные к выполнению задания по теме 2

Вариант

Диаметр трубки 2r₁, мм

Высота ребра

h , мм

Толщина ребра

δ , мм

Скорость движения воздуха w, м/с

Материал ребра

4, 8, 16

1,0; 1,5; 2,0

5, 10, 14, 20

Сталь, Латунь, Медь

2.1 Расчет.

В этой задаче температурный напор Θ_о = t₁ – t_Ж , а уравнение теплового баланса ребра : dQ = Qr – Qr + dr.

Дифференциальное уравнение в цилиндрических координатах выглядит следующим образом:

. (2.1)

Критерий Рейнольдса Re находим по формуле:

, (2.2)

где w – скорость потока воздуха, м/с;

м²/с.

Критерий Нуссельта находим по формуле:

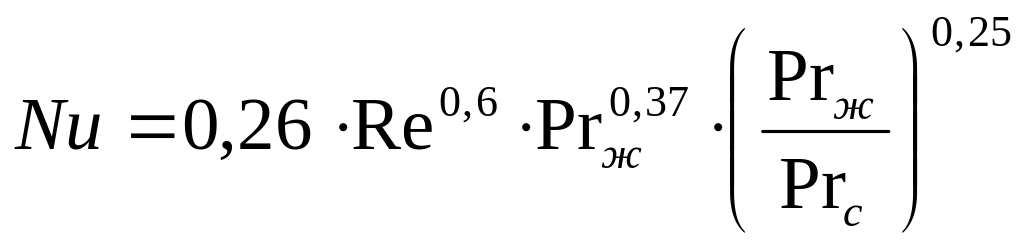, (2.3)

где – критерий Рейнольдса;

=0,705 - критерий Прандтля;

=0,686 - критерий Прандтля.

Коэффициент теплоотдачи от потока пара к поверхности плоской стенки находим по формуле, Вт/м²·К:

, (2.4)

где – критерий Нуссельта;

=2,51·10^-2 Вт/(м·К) - коэффициент теплопроводности;

2r₁=16  10^-3 - диаметр трубки, м;

Т а б л и ц а 2.2

Расчет значения коэффициента Нуссельта, число Рейнольдса и коэффициента теплоотдачи

Параметр	W₁=5 м/с	W₂=10 м/с	W₃= 14м/с	W₄= 20м/с
Nu	41,0191	62,1733	76,0817	94,237
Вт/м²К	64,3486	97,5343	119,3532	147,8343
Re	5649,7175	11299,435	15819,209	22598,87

Параметр m находим по формуле:

, - параметр цилиндрического ребра , 1/м; (2.5)

где λ = 370 Вт/м·К – коэффициент теплопроводности для меди;

λ = 100 Вт/м·К – коэффициент теплопроводности для латуни;

λ = 46 Вт/м·К – коэффициент теплопроводности для стали;

Посчитаем m и полученные результаты сведем в таблицу:

Т а б л и ц а 2.3

Расчет значений параметра ребра

Параметр ребра m, 1/м
Медь	α₁	α₂	α₃	α₄
δ₁	18,6502	22,9611	25,3999	28,2684
δ₂	15,2278	18,7477	20,7389	23,0811
δ₃	13,1877	16,236	17,9604	19,9888

Т а б л и ц а 2.4

Параметр ребра m, 1/м
Латунь	α₁	α₂	α₃	α₄
δ₁	35,8744	44,1666	48,8576	54,3754
δ₂	29,2913	36,0619	39,8921	44,3973
δ₃	25,367	31,2305	34,5475	38,4492

Т а б л и ц а 2.5

Параметр ребра m, 1/м
Сталь	α₁	α₂	α₃	α₄
δ₁	52,8939	65,1201	72,0366	80,1722
δ₂	43,1877	53,1703	58,8176	65,4603
δ₃	37,4016	46,0468	50,9376	56,6903

Температурное поле в кргуглом ребре определяется уравнением Бесселя:

. (2.6)

где I_O – модифицированная функция Бесселя первого рода нулевого порядка,

Y_О – модифицированная функция Бесселя второго рода нулевого порядка,

С₁, С₂ – постоянные интегрирования.

Температурное поле определим по формуле:

. (2.7)

Это есть распределение температуры по телу ребра.

Количество тепла, переданное через основание ребра, можно вычислить по формуле:

, (2.8)

где .

Далее ищем распределение температурного напора  с помощью функций Бесселя. По этому напору находим текущую температуру .

(2.9)

где r₁ и r₂– радиусы в основании вершине ребра, м;

I₁(mr) и Y₁(mr) – соответственно модифицированные функции Бесселя первого и второго рода первого порядка.

где ₀ = t_0. – t_в_. = 120 – 10 = 110C;

t_x = _x + t_о;

Тепловой поток, проходящий через основание ребра, определяется по закону Фурье:

, (2.10)

(2.11)

Рассчитываем эффективность оребрения (табл.№5):

(2.12)

Из (2.12) следует, что коэффициент ребра зависит от его геометрических размеров и параметра m, определяемого коэффициентом теплообмена α и теплопроводными свойствами материала ребра, поэтому при решении задачи следует оценить влияние размеров ребра, интенсивность его теплообмена с взаимодействующим потоком воздуха.

Т а б л и ц а 2.6

Распределение температуры вдоль ребра круглой формы

t,°c	α, Вт/м²К	x,м	Сталь			Латунь			Медь
t,°c	α, Вт/м²К	x,м	δ1,м	δ2,м	δ3,м	δ1,м	δ2,м	δ3,м	δ1,м	δ2,м	δ3,м
h=0,004, м	64,349	r	120	120	120	120	120	120	120	120	120
		r+1/4h	118,72	119,14	119,36	119,41	119,60	119,70	119,84	119,89	119,92
		r+1/2h	117,87	118,57	118,92	119,01	119,34	119,50	119,73	119,82	119,86
		r+3/4h	117,39	118,24	118,68	118,78	119,19	119,39	119,67	119,78	119,83
		r+h	117,23	118,14	118,60	118,71	119,14	119,35	119,65	119,77	119,82
	97,534	0,008	120	120	120	120	120	120	120	120	120
		0,009	118,08	118,71	119,03	119,10	119,40	119,55	119,76	119,84	119,88
		0,01	116,81	117,85	118,38	118,51	119,00	119,25	119,59	119,73	119,80
		0,011	116,08	117,36	118,01	118,17	118,77	119,08	119,50	119,67	119,75
		0,012	115,85	117,20	117,89	118,06	118,70	119,02	119,47	119,65	119,73
	119,353	0,008	120	120	120	120	120	120	120	120	120
		0,009	117,67	118,43	118,81	118,91	119,27	119,45	119,70	119,80	119,85
		0,01	116,12	117,38	118,02	118,18	118,78	119,08	119,50	119,67	119,75
		0,011	115,24	116,78	117,57	117,76	118,50	118,87	119,39	119,59	119,69
		0,012	114,96	116,59	117,43	117,63	118,41	118,80	119,35	119,57	119,67
	147,834	0,008	120	120	120	120	120	120	120	120	120
		0,009	117,14	118,06	118,54	118,65	119,10	119,32	119,63	119,75	119,81
		0,01	115,23	116,77	117,56	117,75	118,49	118,86	119,38	119,59	119,69
		0,011	114,16	116,04	117,01	117,24	118,15	118,60	119,24	119,49	119,62
		0,012	113,81	115,81	116,83	117,08	118,04	118,52	119,20	119,46	119,60
h=0,008, м	64,349	r	120	120	120	120	120	120	120	120	120
		r+1/4h	114,48	116,21	117,12	117,34	118,20	118,64	119,26	119,50	119,63
		r+1/2h	111,03	113,85	115,31	115,67	117,07	117,79	118,79	119,19	119,39
		r+3/4h	109,17	112,56	114,33	114,77	116,46	117,33	118,54	119,02	119,27
		r+h	108,59	112,16	114,03	114,48	116,27	117,18	118,46	118,97	119,23
	97,534	0,008	120	120	120	120	120	120	120	120	120
		0,01	111,97	114,43	115,73	116,05	117,31	117,97	118,88	119,25	119,44
		0,012	106,99	110,95	113,06	113,58	115,63	116,69	118,18	118,78	119,08
		0,014	104,30	109,07	111,61	112,24	114,71	115,99	117,80	118,52	118,89
		0,016	103,47	108,48	111,16	111,82	114,43	115,78	117,68	118,44	118,83
	119,353	0,008	120	120	120	120	120	120	120	120	120
		0,01	110,43	113,30	114,85	115,23	116,74	117,53	118,64	119,09	119,31
		0,012	104,52	109,14	111,63	112,25	114,70	115,98	117,78	118,51	118,88
		0,014	101,33	106,88	109,89	110,64	113,59	115,13	117,32	118,20	118,64
		0,016	100,35	106,19	109,35	110,14	113,25	114,87	117,17	118,10	118,57
	147,834	0,008	120	120	120	120	120	120	120	120	120
		0,01	108,53	111,90	113,73	114,19	116,01	116,96	118,32	118,87	119,15
		0,012	101,48	106,87	109,83	110,57	113,52	115,06	117,27	118,16	118,62
		0,014	97,70	104,16	107,72	108,61	112,16	114,03	116,70	117,78	118,33
		0,016	96,53	103,32	107,07	108,00	111,74	113,71	116,52	117,66	118,23

Продолжение таблицы 2.6

h=0,016, м	64,349	r	120	120	120	120	120	120	120	120	120
		r+1/4h	99,14	104,57	107,75	108,57	111,94	113,77	116,49	117,62	118,20
		r+1/2h	87,80	96,07	100,96	102,22	107,43	110,28	114,51	116,27	117,18
		r+3/4h	82,13	91,77	97,51	98,99	105,12	108,49	113,49	115,58	116,65
		r+h	80,44	90,49	96,47	98,02	104,43	107,95	113,18	115,37	116,50
	97,534	0,008	120	120	120	120	120	120	120	120	120
		0,012	92,52	98,99	102,98	104,03	108,47	110,98	114,81	116,45	117,30
		0,016	77,88	87,57	93,63	95,23	102,07	105,94	111,90	114,45	115,78
		0,02	70,67	81,86	88,92	90,80	98,81	103,37	110,40	113,43	115,00
		0,024	68,54	80,16	87,51	89,47	97,84	102,60	109,95	113,12	114,77
	119,353	0,008	120	120	120	120	120	120	120	120	120
		0,012	89,00	95,88	100,24	101,40	106,40	109,27	113,76	115,71	116,73
		0,016	72,71	82,89	89,46	91,23	98,87	103,30	110,25	113,29	114,89
		0,02	64,75	76,44	84,05	86,11	95,05	100,26	108,46	112,05	113,94
		0,024	62,42	74,53	82,45	84,59	93,92	99,36	107,92	111,68	113,65
	147,834	0,008	120	120	120	120	120	120	120	120	120
		0,012	85,11	92,34	97,04	98,32	103,90	107,19	112,43	114,76	116,00
		0,016	67,09	77,62	84,64	86,56	95,04	100,08	108,19	111,82	113,74
		0,02	58,39	70,36	78,45	80,68	90,56	96,48	106,03	110,31	112,58
		0,024	55,86	68,23	76,62	78,94	89,23	95,40	105,38	109,86	112,23

Т а б л и ц а 2.7

Расчет теплового потока, проходящего через основание ребра Q₀

Q₀,Вт	α, Вт/м²К	Сталь			Латунь			Медь
Q₀,Вт	α, Вт/м²К	δ1,м	δ2,м	δ3,м	δ1,м	δ2,м	δ3,м	δ1,м	δ2,м	δ3,м
h=0,004, м	64,349	3,492	3,513	3,524	3,526	3,536	3,541	3,548	3,551	3,552
	97,534	5,245	5,292	5,316	5,322	5,345	5,356	5,372	5,378	5,381
	119,353	6,38	6,45	6,486	6,495	6,528	6,545	6,568	6,577	6,582
	147,834	7,842	7,948	8,002	8,015	8,066	8,092	8,127	8,142	8,149
h=0,008, м	64,349	7,875	8,082	8,19	8,216	8,319	8,372	8,446	8,475	8,49
	97,534	11,49	11,93	12,16	12,22	12,45	12,57	12,73	12,8	12,83
	119,353	13,72	14,35	14,69	14,77	15,11	15,28	15,53	15,63	15,68
	147,834	16,48	17,39	17,89	18,01	18,51	18,77	19,15	19,3	19,37
h=0,016, м	64,349	16,28	17,94	18,92	19,18	20,22	20,8	21,65	22,01	22,19
	97,534	21,68	24,61	26,45	26,94	29,02	30,2	32,02	32,8	33,21
	119,353	24,62	28,38	30,82	31,47	34,32	35,97	38,57	39,7	40,3
	147,834	27,94	32,74	35,95	36,84	40,74	43,07	46,82	48,5	49,39

Т а б л и ц а 2.8

Расчет коэффициента эффективности круглого ребра Е

E	α, Вт/м²К	Сталь			Латунь			Медь
E	α, Вт/м²К	δ1,м	δ2,м	δ3,м	δ1,м	δ2,м	δ3,м	δ1,м	δ2,м	δ3,м
h=0,004, м	64,349	0,9821	0,9880	0,9909	0,9917	0,9944	0,9958	0,9977	0,9985	0,9989
	97,534	0,9731	0,9819	0,9863	0,9874	0,9916	0,9937	0,9966	0,9977	0,9983
	119,353	0,9673	0,9779	0,9833	0,9846	0,9897	0,9923	0,9958	0,9972	0,9979
	147,834	0,9599	0,9728	0,9795	0,9811	0,9873	0,9904	0,9948	0,9965	0,9974
h=0,008, м	64,349	0,9227	0,9469	0,9596	0,9627	0,9747	0,9809	0,9896	0,9930	0,9948
	97,534	0,8878	0,9219	0,9401	0,9446	0,9623	0,9714	0,9843	0,9895	0,9921
	119,353	0,8665	0,9063	0,9278	0,9332	0,9543	0,9653	0,9809	0,9872	0,9903
	147,834	0,8404	0,8868	0,9123	0,9187	0,9441	0,9574	0,9764	0,9841	0,9881
h=0,016, м	64,349	0,7154	0,7883	0,8314	0,8426	0,8886	0,9138	0,9513	0,9669	0,9750
	97,534	0,6284	0,7134	0,7667	0,7809	0,8412	0,8755	0,9282	0,9508	0,9626
	119,353	0,5832	0,6723	0,7300	0,7456	0,8130	0,8521	0,9136	0,9405	0,9547
	147,834	0,5344	0,6261	0,6876	0,7045	0,7792	0,8237	0,8954	0,9275	0,9445

<<< < Предыдущая 1 23 / 63 4 5 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
09.04.20151.07 Mб110teor_ver_1 (1).doc
#
10.04.20152.07 Mб5Teplyakov_A.doc
#
01.05.2025170.37 Кб0Testy_MSiS,, 1 блок.docx
#
01.05.2025173.92 Кб0Testy_MSiS,, 1 блок.docx
#
09.04.20159.6 Mб128tlets_test.doc
#
01.05.20253.14 Mб0Tmo_kursovik.doc
#
15.03.201643.57 Кб32Transportnaya_bezopasnost (1).docx
#
10.04.201546.59 Кб27Trebovania_k_oformleniyu_referata.doc
#
10.04.20152.02 Mб7UdalcovKONSTR.pdf
#
01.05.202526.33 Кб0UK_12_chetn.docx
#
01.05.2025137.22 Кб0Upravlenie_potokami_na_sklade (1).doc