
Тестирование
Запустите программу и введите значение
x=3
Проверьте, результат должен быть следующим:
значение выражения=0.355556
Заполните таблицу
x
Значение выражения
1
1
2
0.2
3
-0.5
Добавьте в таблицу свои значения x. Подберите такие значения x, чтобы получить значение суммы больше 100, меньше -100.
Подберите два таких значения x (положительное и отрицательное), чтобы выполнялось неравенство |S|<10-3
Как описать функцию f, не используя описаний для функций min и max. Какое из решений оптимальное? Почему?
Индивидуальные задания.
Дано действительное число x. Получить
f(2x,
3) +
f(3,
5 –
x),
где
f(a,
b)=![]() ;
;
Даны действительные числа s и t. Получить
f(1,
s)
+
f(t,
2)
где
f(a,
b)=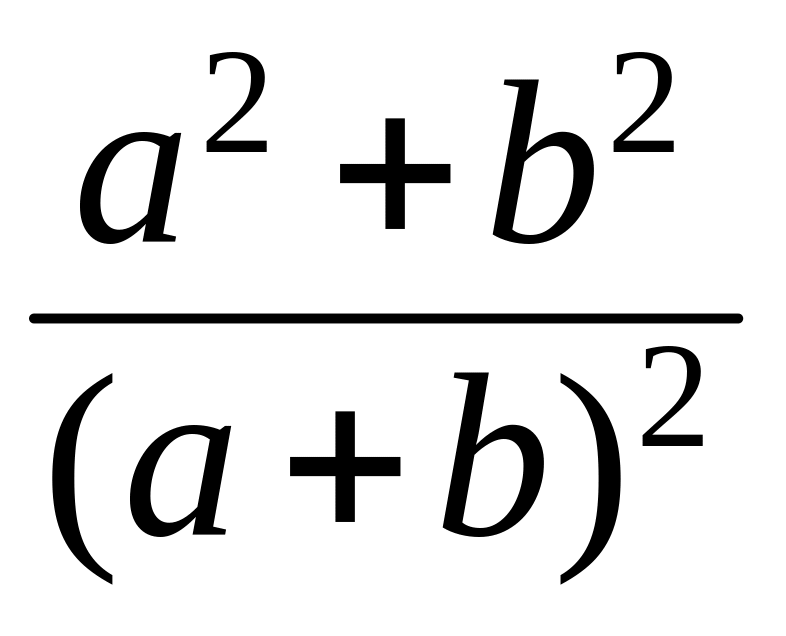 ;
;
Даны действительные числа s и t. Получить
f(t,
–2s,
1.17) +
f(2.2,
t,
t
–
s),
где
f(a,
b,
c)=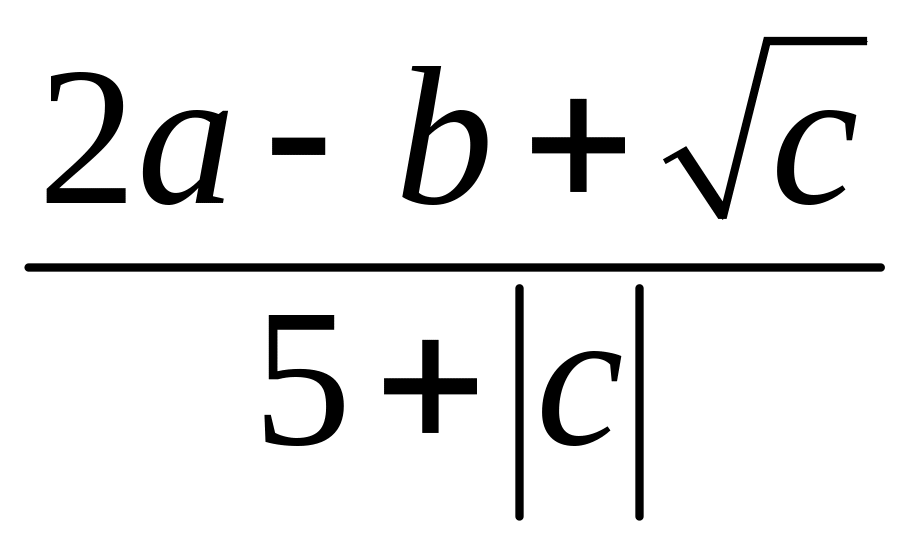 ;
;
Даны действительные числа s и t. Получить
f(1.2,
s)
+
f(t,
s)
–
f(2s
–
1, st),
где
f(a,
b)=![]() ;
;
Даны действительные числа s и t. Получить
f(t,
–2s)
+
f(2t,
t
–
s),
где
f(a,
c)=![]() ;
;
Даны а, b. Получить
![]()
Даны а, b. Получить
![]()
Даны а, b, c. Получить
![]() ;
;
Даны а, b, c. Получить
![]() ;
;
Даны действительные числа s и t. Получить
![]() ,
,
где
f(a,
b)
=![]() +
+![]() +
(a
–
b)3
+
(a
–
b)3
Даны действительные числа s, t, v. Получить
![]() ,
,
где
f(a,
b)
=![]() +
(a–b)2
,
r(a,
b)
=
+
(a–b)2
,
r(a,
b)
=![]() +
(a–b)2.
+
(a–b)2.
Дано действительное число y. Получить
![]() ,
где f(x,
k)
=
,
где f(x,
k)
=![]()
Задание 3. Написать программу для решения геометрической задачи.
Образец выполнения задания.
Задача: Выпуклый четырехугольник задан координатами своих вершин. Найти периметр и площадь четырехугольника. Вычисление длины отрезка и площади треугольника оформить в виде подпрограмм.
Этапы выполнения задания.
Определение исходных данных: x1, y1, x2, y2, x3, y3, x4, y4 (координаты вершин).
Определение результатов: P и S – периметр и площадь четырехугольника.
Алгоритм решения задачи.
Ввод исходных данных.
Периметр четырехугольника – сумма длин его сторон. Длина стороны – длина отрезка, соединяющего вершины. Вычисление длины отрезка оформляем в виде функции dlin.
Д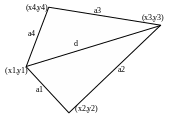 ля
вычисления площади проведем диагональ,
соединяющую вершины с координатами
(x1,y1)
и (x3,y3)
(или (x2,y2)
и (x4,y4)),
четырехугольник разобьется на два
треугольника. Площадь четырехугольника
– сумма площадей двух треугольников.
Для вычисления площади треугольника
оно воспользоваться формулой Герона,
так как для треугольников известны
длины сторон. Обозначения вспомогательных
переменных смотри на рисунке. Вычисление
площади треугольника оформляем в виде
функции plos.
ля
вычисления площади проведем диагональ,
соединяющую вершины с координатами
(x1,y1)
и (x3,y3)
(или (x2,y2)
и (x4,y4)),
четырехугольник разобьется на два
треугольника. Площадь четырехугольника
– сумма площадей двух треугольников.
Для вычисления площади треугольника
оно воспользоваться формулой Герона,
так как для треугольников известны
длины сторон. Обозначения вспомогательных
переменных смотри на рисунке. Вычисление
площади треугольника оформляем в виде
функции plos.
Вывод результата.
Описание переменных:
Все переменные в программе имеют тип double.
Программа:
#include <iostream>
#include <math.h>
#include <windows.h>
using namespace std;
double dlin(double x,double y,double x0, double y0)
{ double d=sqrt(pow((x-x0),2)+pow((y-y0),2));
return d;
}
double plos(double a, double b, double c)
{ double pr=(a+b+c)/2;
double pl=sqrt(pr*(pr-a)*(pr-b)*(pr-c));
return pl;
}
int main()
{
SetConsoleCP(1251);
SetConsoleOutputCP(1251);
double x1,y1,x2,y2,x3,y3,x4,y4,a1,a2,a3,a4,p,s1,s2,d,s;
cout << "введите координаты вершины 1 - ";
cin>>x1>>y1;
cout << "введите координаты вершины 2 - ";
cin>>x2>>y2;
cout << "введите координаты вершины 3 - ";
cin>>x3>>y3;
cout << "введите координаты вершины 4 - ";
cin>>x4>>y4;
a1=dlin(x1,y1,x2,y2);
a2=dlin(x2,y2,x3,y3);
a3=dlin(x3,y3,x4,y4);
a4=dlin(x4,y4,x1,y1);
d=dlin(x1,y1,x3,y3);
p=a1+a2+a3+a4;
s1=plos(a1,a2,d);
s2=plos(a3,a4,d);
s=s1+s2;
cout<<"периметр="<<p<<endl;
cout<<"площадь="<<s<<endl;
}
