3.3.2. Електроно-ядерна спінова система донорного атома в магнітному полі

Ядерний і електронний спіни донорного атома, що знаходиться в основному орбітальному стані , взаємодіють між собою за допомогою надтонкої і диполь-дипольної магнітної взаємодії. Проте останнє, після усереднення по орбітальному електронному S-стану, перетворюється в нуль і залишається лише надтонка взаємодія, спіновий гамільтоніан який в системі одиниць СІ визначається формулою Фермі (F. Fermi) у вигляді:

де

- константа надтонкої взаємодії, - ядерний магнетон, і для ³¹P_{g N} = 2,26. За допомогою експериментально знайденого значення постійної надтонкої взаємодії [5.6] , для ймовірності нахожденя електрона на ядрі донора (координата г = 0), отримаємо .

Спіновий електроно-ядерний гамільтоніан для донорного атома має вигляд:

чотири енергетичних рівня якого описуються формулою Брей-та-Рабі (G. Вгеit, I. Rabi) [5.7], яка для I = S = 1/2 (вісь z паралельна В) має вигляд:

де F = I ± 1/ 2 = 1, 0, при цьому M_F = M + m = ± 1, 0 при F = 1 i M_F = 0 при F = 0, М, m - власні значення операторів . Залежність енергетичних рівнів від X показана на рис. 5.2.

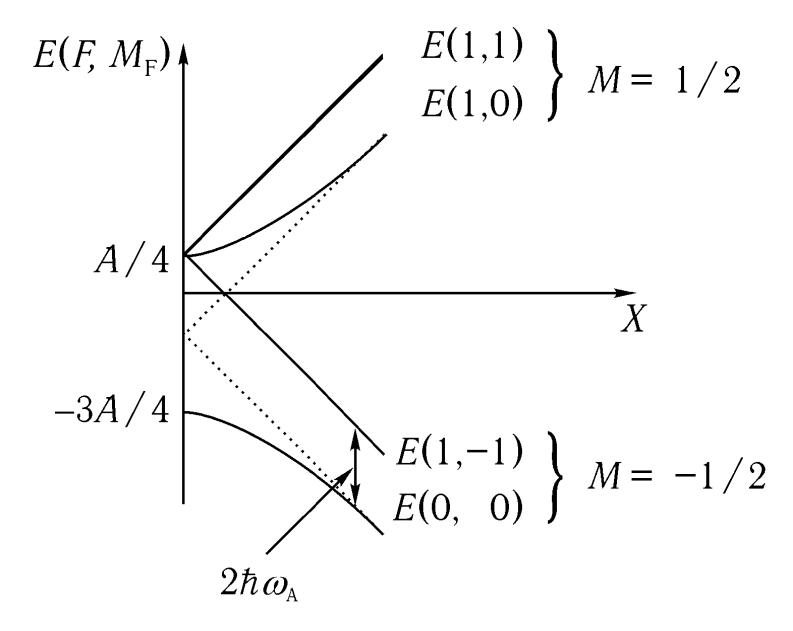
Рис. 5.2. Схема енергетичних рівнів електроно-ядерної спінової системи донорного атома.

Для енергії основного спінового стану F = 0, М_F = 0 (М = -1 / 2, m = 1/2) отримаємо

Наступний збуджений енергетичний рівень відповідає стану F = 1, М_F = -1 з іншим станом ядерного спина (М = -1 / 2, m = -1 / 2):

.

Таким чином, різниця енергій двох станів ядерного спiна, що взаємодіє з електроном донорного атома, не змінюючи свого стану, має простий вигляд (при ,

):

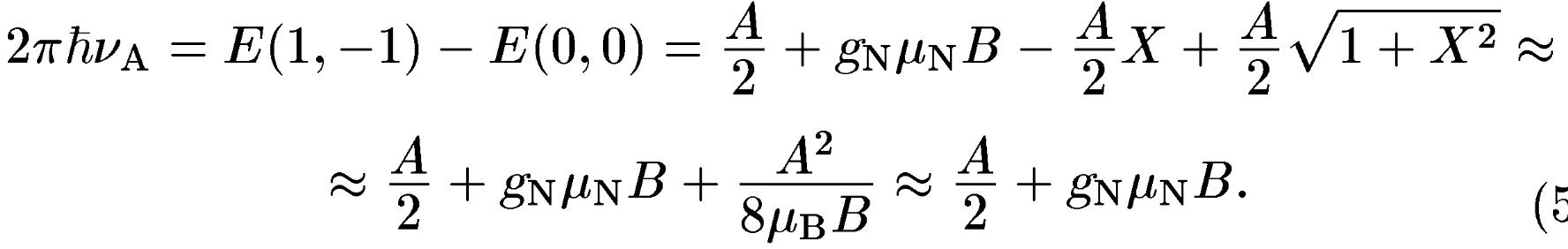
Для донорних атомів ³¹P перший доданок в (5.7) перевищує другий в полях В < 3,5 Тл. У цьому випадку ядерна резонансна частота визначається переважно стаціонарним локальним магнітним полем, створюваним на ядрі електронної спінової поляризацією.

Стан в базисі М, m еквівалентнa стану , а стан є в цьому ж базисі суперпозицією станів наступного виду:

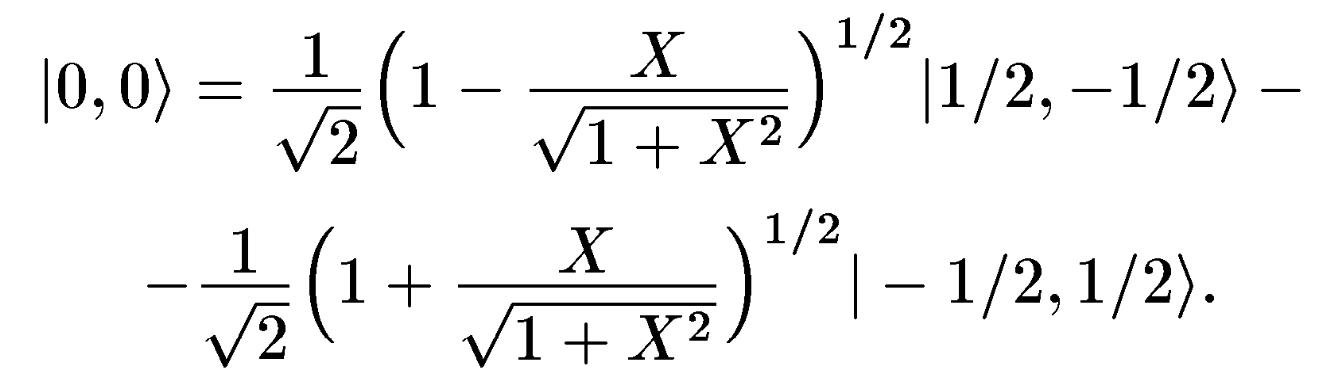
Резонансна частота Рабі , відповідна переходам між станами (рис. 5.2), визначається матричним елементом від гамильтониіана взаємодії з обертовим з резонансною частотою v_A в перпендикулярній зовнішньому полю площині радіочастотнe поле з амплітудою b:

де

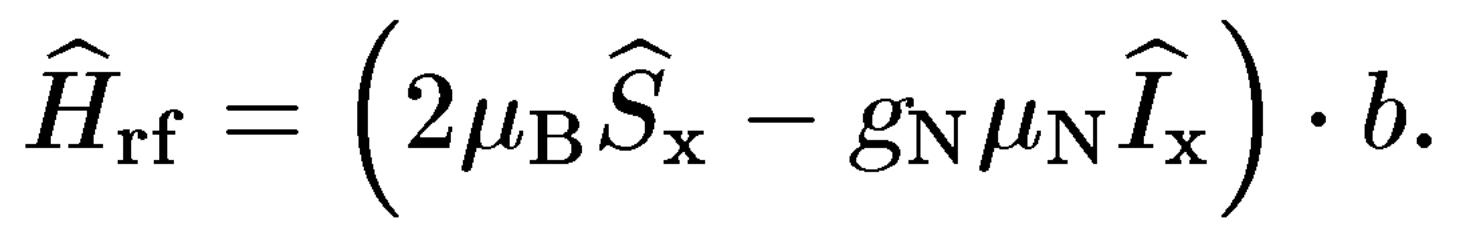
Для ефективного гіромагнітного відношення отримаємо

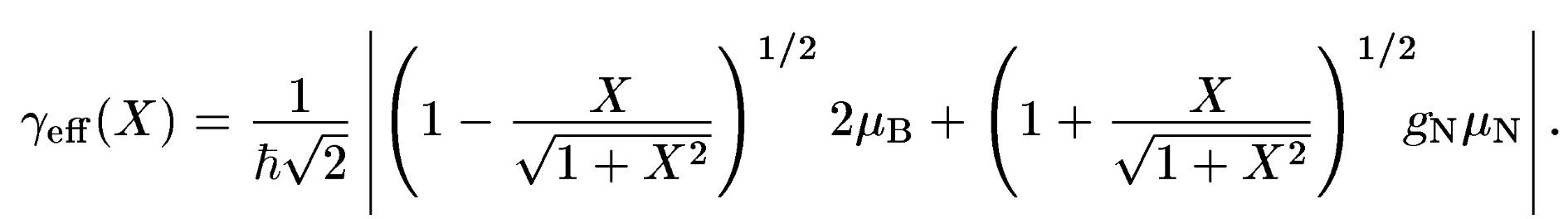
Частота Рабі має максимальне значення при X = 0 з і швидко монотонно зменшується до значення, відповідно існуючому ізольованому (А => 0) ядерного спіна . Тому з точки зору швидкості виконання квантових операцій, яка визначається частотою Рабі, бажано працювати в області малих зовнішніх полів, при яких X < 1. Це, крім того, дозволить зменшити вплив поля на сусідні напівпровідникові пристрої.

При значеннях радіочастотне поле в процесі ЯМР впливає не небезпосередньо на ядерний спін, а через поперечну складову електронної поляризації. В результаті ядерний спін відчуває набагато більш сильне змінне локальне магнітне поле в порівнянні з зовнішнім радіочастотним полем. На таке посилення сигналу ядерного резонансу в парамагнітних системах, як уже зазначалося, було зазначено в роботі Валієва [5.8].

Далі, використовуючи [5.1], приймемо В = 2Тл і для ядерної резонансної частоти отримаємо