3.2.2. Двохкубітовий вентиль сnot. Приклади його реалізації

Основним двухкубитовий вентилем, як зазначалося вже, є операція СNOT, яку можна записати в матричній формі наступним чином:

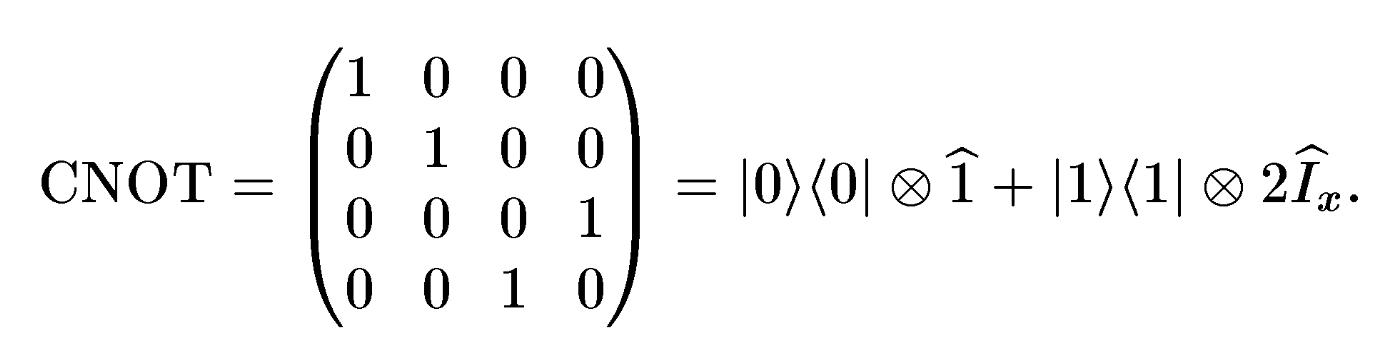
Результат дії операції СNOT на два кубіта полягає в тому, що перший кубіт не змінює свого стану, а другий змінює його тільки якщо перший кубіт перебував у стані | 1). Для того, щоб можна було здійснити цю операцію істотна наявність взаємодії між кубытами. Спін-спінова взаємодія між ядерними спынами в гамільтоніані (4.5) якраз і здатне забезчити відповідне перетворення.

Існують різні способи реалізації операції СNOT. Найбільш прямим є використання імпульсів, селективним образом збуджуючих один з спінив, коли другий залишається в одному з двох власних станів. Цим двом станам другого спіна відповідають два переходи, з різними внаслідок спін-спінової взаємодії енергій. Фактично цей спосіб аналогічний відомому методу подвійного резонансу Паунда-Оверхаузера (R. Pound, A. Overhauser) [4.4, 4.10]. Нижче на конкретних прикладах буде продемонстрований цей спосіб.

Інший більш загальний спосіб заснований на використанні багатоімпульсній техніки. Операція СNOT була представлена у вигляді квантової схеми:

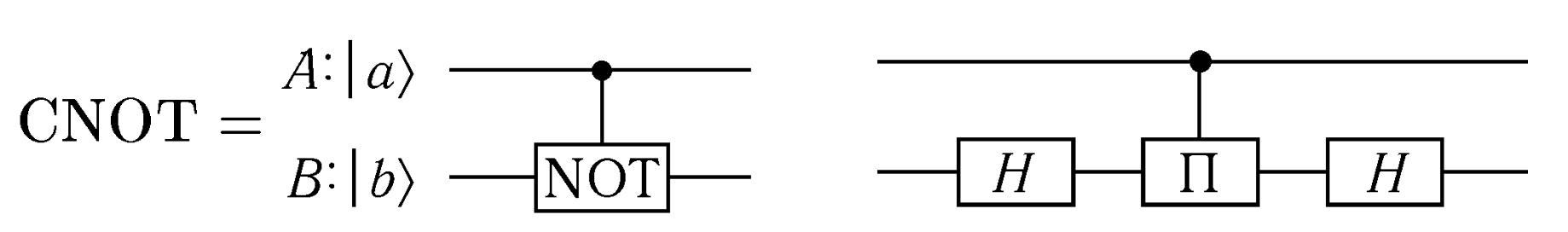
Однак при її реалізації зручніше скористатися іншою еквівалентною схемою, в якій оператори Адамара Н замінюються прямим і оберненим самоперевідним псевдооператор Адамара [4.13]

які відповідають більш простий операцій повороту на кут ± ПІ / 2 навколо осі у: . Квантова схема для оператора СNOT при цьому приймає наступний вигляд (операції в послідовності зліва направо):

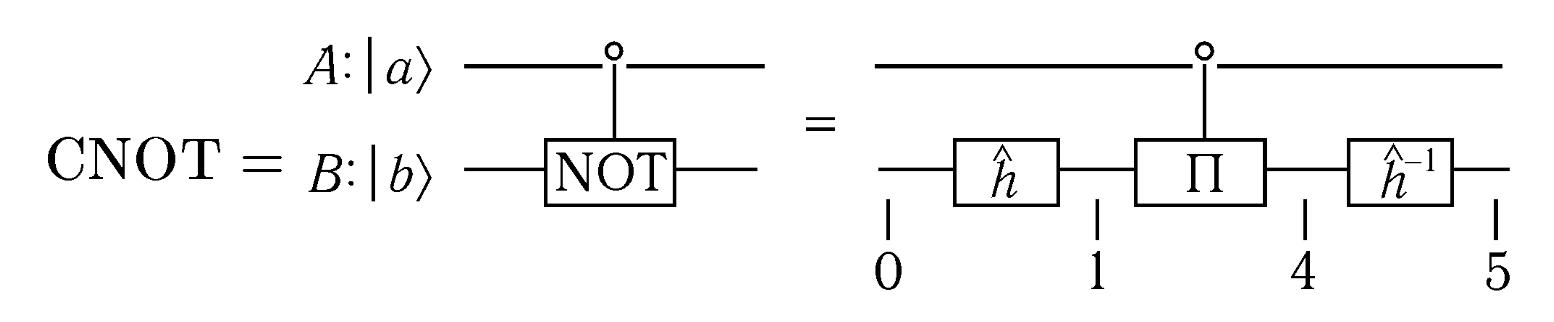
Розглянемо тепер один із способів здійснення операції СNOT за допомогою імпульсної техніки ЯМР [4.1]. Для цього, згідно (4.33), слід провести наступну послідовність операцій, що діють на контролюючий А і контрольований В спіни-кубіти (у послідовності справа наліво), тобто

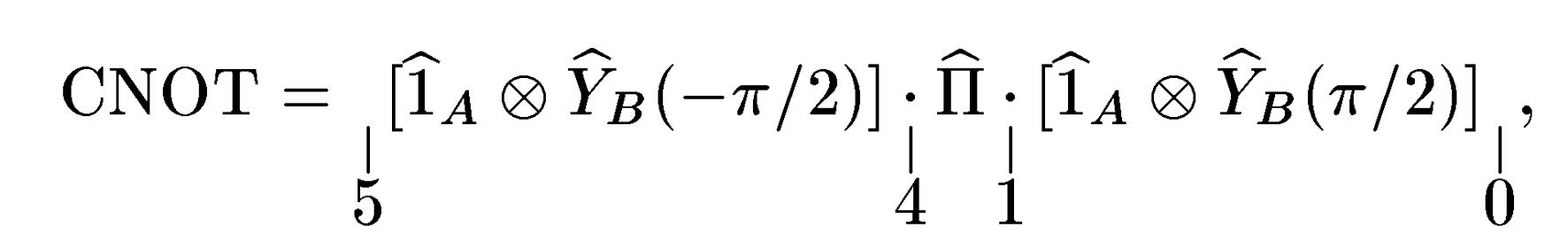
де оператор контрольованої зміни фази стану з урахуванням (4.16), (4.18) і (4.24) може бути представлений у вигляді добутку наступних трьох комутуючих матриць повороту [4.1]:

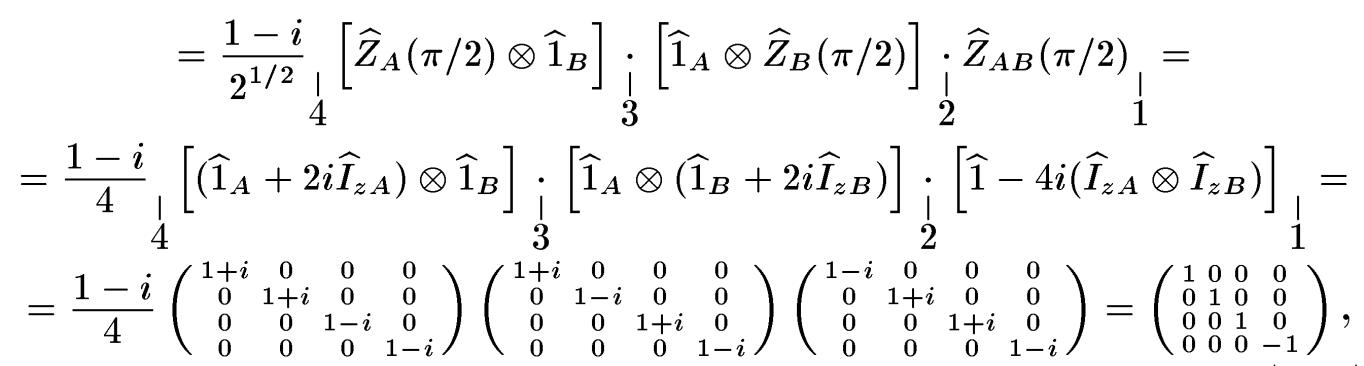
де цифрами відзначені послідовні моменти часу, відповідні границям між окремими операціями у виразах (4.33) - (4.35).

Проста векторна модель, яка пояснює наочно дію послідовності п'яти зазначених операцій, представлена ​​на рис. 4.4 [4.1], з якого видно, що перевертання в кінці всього процесу (момент 5) контрольованого спіна В відбувається, тільки коли контролюючий спін А знаходиться в стані . В інтервалі 1-2 діє двохкубітовий оператор , який здійснює, у відповідності з (4.21), поворот х-складової оператора спіна В навколо осі z на кут -ПІ / 2 при стані спина або на кут ПІ / 2 при . Усі інші операції здійснюються за допомогою однокубітових операцій повороту з спінами А і В.

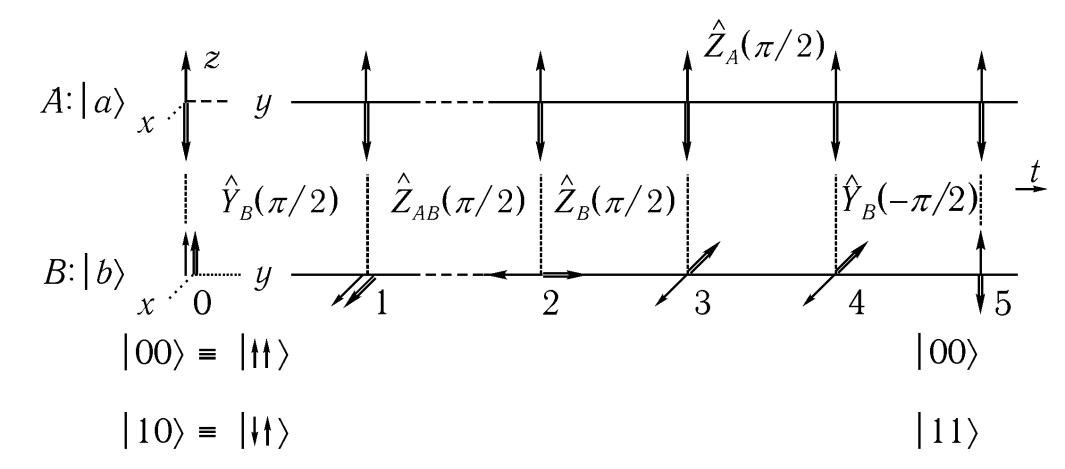
Рис. 4.4. Проста векторна модель С] чот, що ілюструє дію п'яти імпульсів при абсолютному нулі температур [4.1]. Представлені два випадки на вході: стан | 00) (жирні вектори) і стан 110) (вектори з подв ¬ ної лінією). Прецессия вектора спина А в зовнішньому полі В в цій моделі, як і операції 2 А, незображується.

Оператор СNOT у формі (4.34), (4.35) можна представити в іншому більш зручному вигляді. Переставимо для цього місцями операції в двох квадратних дужках в інтервалі 2-5 і врахуємо властивість прямих добутків

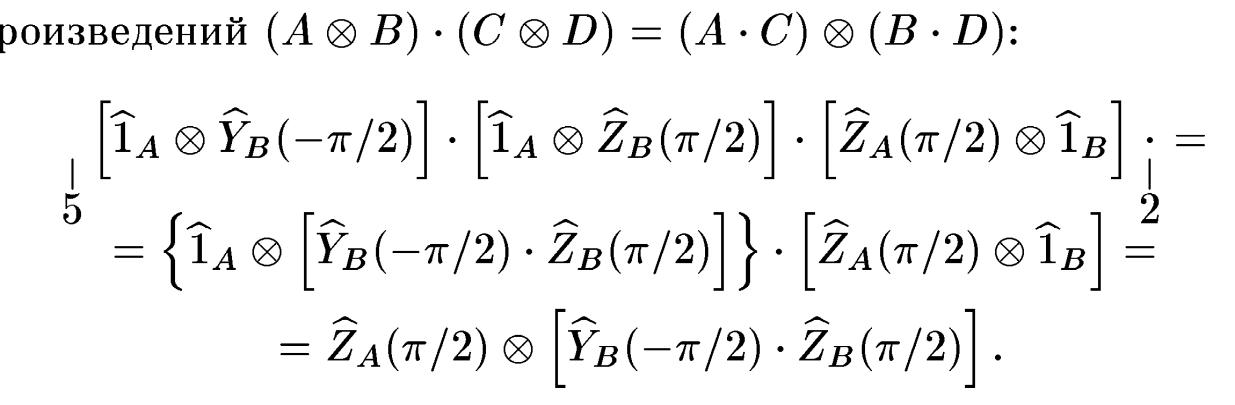
У результаті операція СNОТ тепер буде описується наступною послідовністю з п'яти незалежних операцій:

Оператори повороту в (4.37) можуть здійснювати, як уже зазначалося, за рахунок вільної прецесії спінів А і В у зовнішньому постійному магнітному полі при відсутності радіочастотних імпульсів. Але в цьому випадку ця прецесія повина «включатися» протягом наступних один за одним зі своїм початком відліку проміжків часу порядку чверті періоду вільної прецесії , тобто дуже коротких у порівняні з тривалістю операцій , які порядку , що, очевидно, практично неможливо. Тому операції повороту навколо осі z слід здійснювати за допомогою послідовності трьох селективних радіочастотних імпульсів. Використовуючи вираз (4.25), знайдемо

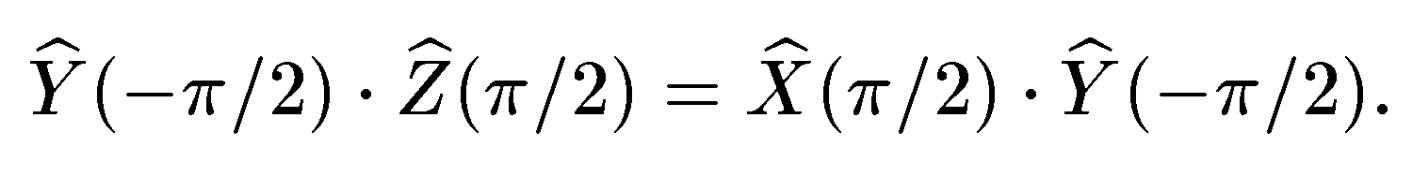
Враховуючи співвідношення (4.25), (4.38) і властивість прямих добутків, замість (4.37) отримаємо тепер послідовність семи операцій, що не містить зовсім операцій повороту :

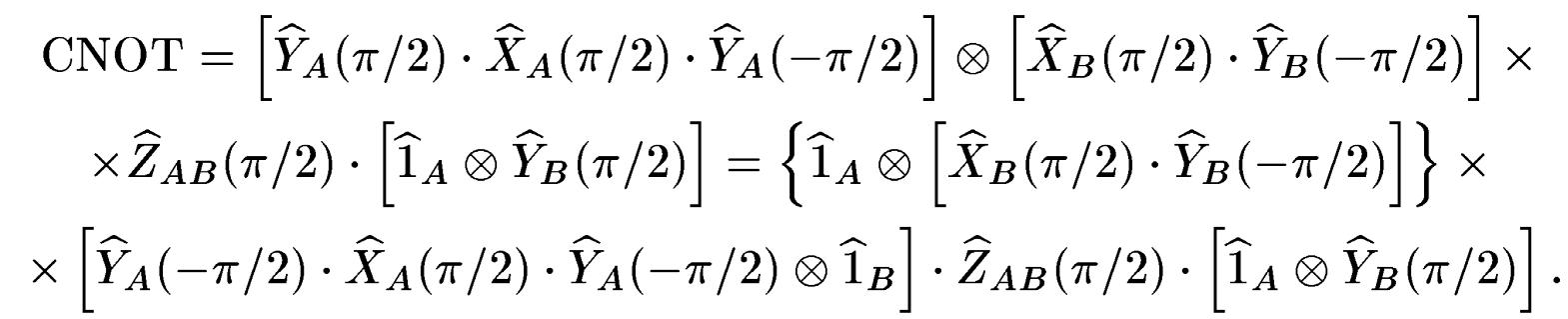
Її можна переписати інакше (такого типу послідовність приводиться, наприклад, в [4.15])

де операція представляє собою одночасний поворот на --ПІ / 2 обох спінив А і В навколо осі у в результаті дії двох селективних або одного неселектівного (nonselective, «hard») імпульсу. Останнє можливо, якщо ширина частотного спектра імпульсів перекриває резонансні частоти обох ядерних спінів.

Зауважимо, що негативні кути повороту -ПІ / 2 для операторів спина еквівалентні, як і для класичних векторів позитивним кутам (двокомпонентні хвильові функції - Спінор, як відомо, при зміні фази на 2п змінюють знак! ). Мінімальний час повороту оператора спина В і аналогічно спіна А навколо осі z на -ПІ / 2 тепер визначається тривалістю трьох радіочастотних імпульсів з позитивними кутами поворотів , яка при значно більше періоду вільної прецесії .