3.2. Формування квантових вентилів методами ямр

3.2.1. Однокубітові квантові операції

У порівнянні з процесом ініціалізації формування квантових вентилів у ЯМР квантових комп'ютерах виявляється порівняно простим, воно грунтується на добре розроблених імпульсних методах в ЯМР спектроскопії [4.10-4.12]. Нагадаємо перш за все деякі необхідні для подальшого відомості з теорії магнітного резонансу, які в рівній мірі відносяться як до ядерних, так і до електронних спінів. Найбільш простий спосіб опису однокубітової операцій полягає у використанні векторної моделі Блоха, в якій стан спінакубіта представляється точкою на сфері Блоха, а однокубітові операції під дією радіочастотних імпульсів як повороти класичного вектора Блоха, що вказує на цю точку. Однак тут буде використано більш загальний квантовий опис, воно буде необхідним далі для опису двохкубітових квантових операцій, для яких простої векторної моделі не існує.

Гамільтоніан вільного ядерного спина I_A= 1/2 з гіромагнітного відношення 7а у постійному полі В (вісь z) має вигляд Вільна прецесія спіна в цьому полі з частотою описується, як відомо , унітарним оператором правого повороту оператора спіна навколо осі z на кут :

Оператор еволюції в часі пари взаємодіючих спінів, описуваний комутуючим з операторами гамільтоніаном (4.5), можна представити як три незалежні оператора: два оператори повороту навколо осі z спінів А і В у постійному зовнішньому полі (матриці 2x2: ) і оператор повороту, обумовлений взаємодією спінів (матриця 4x4: ):

де

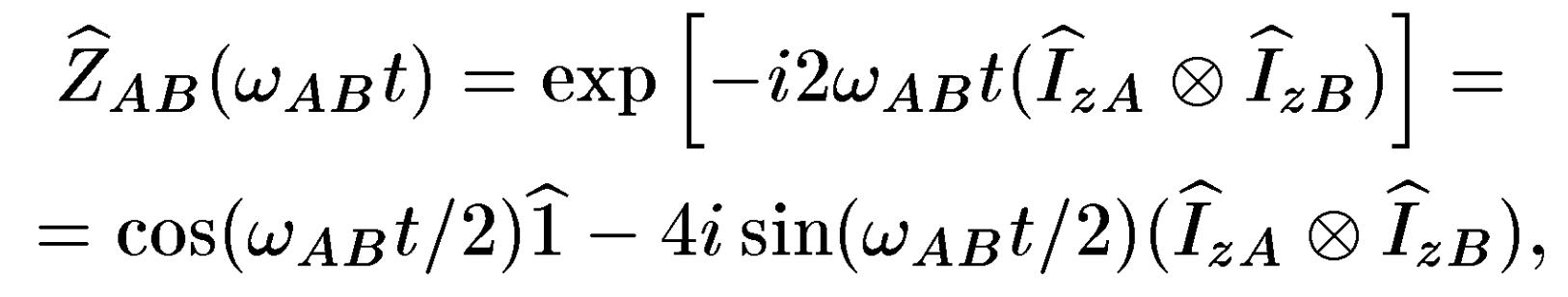
де 1 - одинична чотирирядна матриця.

Еволюція в часі оператора спина описується виразом

Зокрема, в результаті дії оператора на оператор частини спіна відбувається поворот її на кут

а в результаті дії оператора - поворот складової отримаємо на кут :

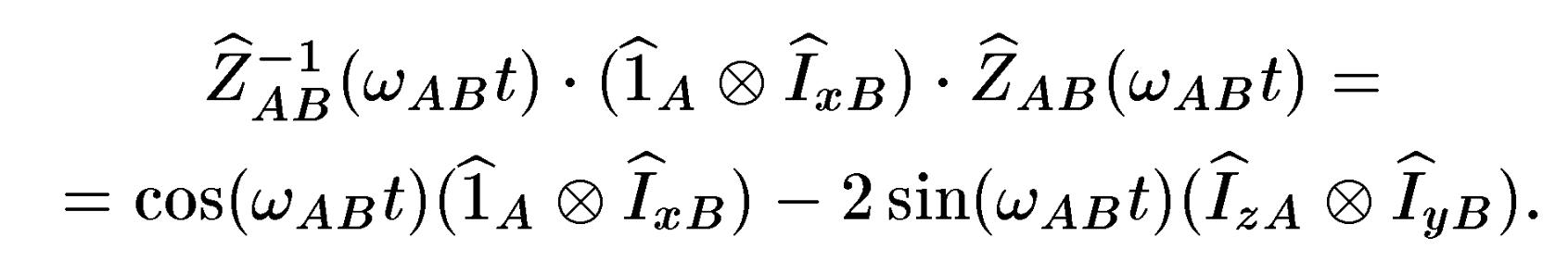
З останнього виразу випливає, що операція (4.21) при відповідає лівому або правому повороту поперечної складової оператора спина на кут в залежності від стану спина А: .

Імпульс радіочастотного поля в простому випадку має одну поляризовану по колу складову (вона створюється двома перпендикулярними одна одній котушками) видання в площині перпендикулярній зовнішньому полю В = Вк (i, j, k - орти в напрямку осей x, y, z), з амплітудою b << B, з резонансною для розглянутого спина А частотою w=w_A і тривалістю імпульсу ^t>>1/ w_A . Якщо перейти з лабораторної системи у обертову з частотою w навколо осі z систему координат, в якій вектор b=bi протягом тривалості імпульсу не залежить від часу, то спін буде прецессировать навколо напрямку цього вектора з частотою , названої резонансною частотою Рабі. Радіочастотний імпульс справить поворот спіна навколо напрямку вектора b=bi (косинус-імпульс) на кут - площа прямокутного імпульсу). Відповідний унітарний оператор в обертовій системі координат має вигляд:

Операція повороту навколо осі у здійснюється резонансним імпульсом зрушеним за фазою на (синус-імпульс), для якого .

Зокрема, операції повороту навколо осей х, у під дією імпульсів на кут представляються матрицями вигляду:

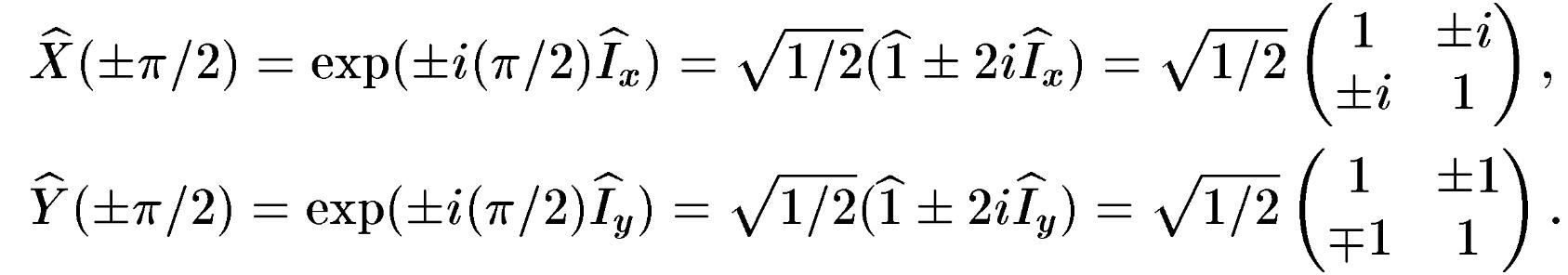
Тривалість відповідного імпульсу . При досить великій різниці резонансних частот [w_A – w_B] в порівнянні з шириною спектру радіочастотного імпульсу, яка порядку частоти Рабі (селективний (selective, «soft») імпульс) можлива індивідуальна резонансна настройка на один спін, без істотної зміни стану іншого спіна . Операція повороту на кут навколо осі z, описувана виразом

виконується за рахунок природного процесу вільної прецесії спіна в зовнішньому полі В за час у відсутності радіочастотного імпульсу.

Однак як буде видно з подальшого, зручніше здійснювати її за допомогою послідовності трьох діючих на спини селективних радіочастотних імпульсів, що виконують послідовні повороти навколо осей х і у в обертовій з резонансною частотою системі координат. Так, використовуючи вирази (4.23), (4.24), неважко переконатися, що

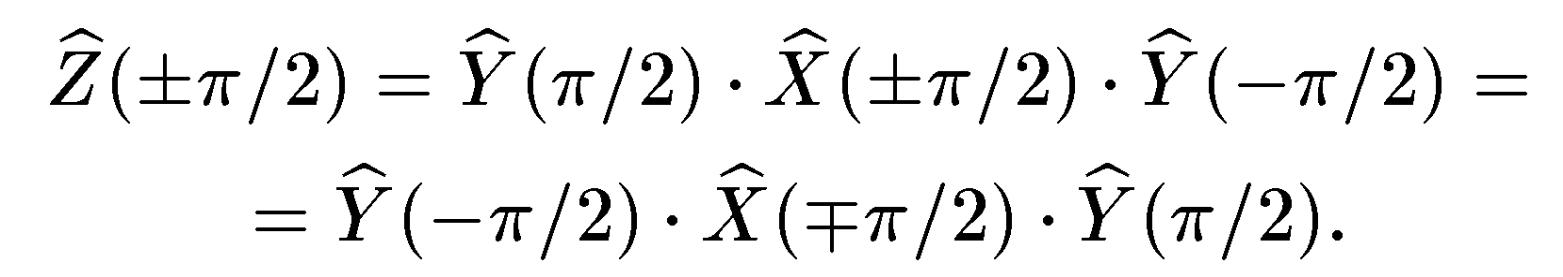
Перейдемо тепер до розгляду основних однокубітових квантових вентилів, перетворюючих, стан окремого ядерного спина. Таким є, зокрема, однокубітовий оборотний вентиль НЕ (NOT). Операція над ядерним спіном, відповідному такому вентилю, здійснюється унітарним оператором, що виробляють поворот в спіновім просторі одного спіна навколо осі х на кут = ПІ, тобто

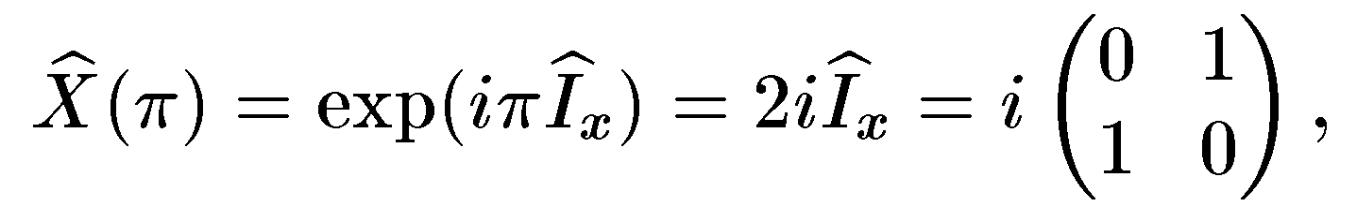
який відрізняється від оператора NOT несуттєвим постійним фазовим множником i.

Іншим однокубітовим вентилем є оператор Адамара Н. Йому відповідає унітарний оператор, що відрізняється від самоперевідного оператора Адамара також несуттєвим множником,

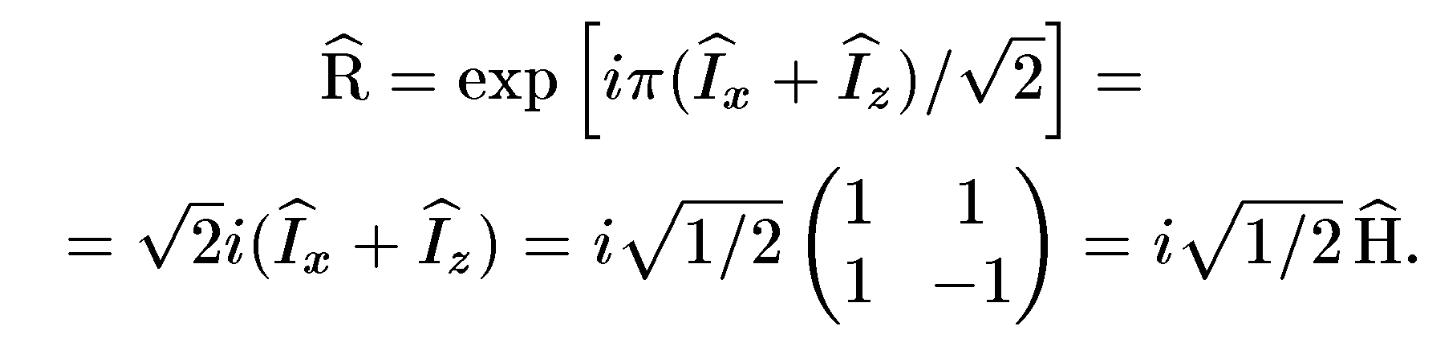
Він визначає операцію повороту на кут ПІ навколо напрямку i+k, що може бути досягнуто шляхом впливу нерезонансного імпульсу з частотою або послідовності трьох імпульсів (трьохімпульсний сендвіч), що здійснюють повороти на кут -ПИ / 4 навколо осі у , на ПИ навколо осі х і на ПИ/ 4 навколо осі у [4.12, 4.13]:

Ще однією однокубітовой операцією є селективна декогерентізація стану кубітів в ансамблі, здійснювана за допомогою імпульсів градієнта магнітного поля. Ця операція використовується, наприклад, при приготуванні квазічістого початкового стану методом просторового усереднення. Оператор повороту і-го спіна в ансамблі навколо осі z під дією імпульсу градієнта постійного поля вздовж осі zdВ / dz = G = соnst і тривалістю ^t має вигляд:

Усереднення по ансамблю, якщо припускати гаусівський розподіл відхилень координат спінів , де D - коефіцієнт спінової дифузії, приводить до відомого з теорії спінового еха результату [4.14]:

Когерентні (недіагональні) елементи однокубітової матриці густини під дією такої операції загасають, тобто має місце рефокусіровка або декогерентізація однокубітових станів з характерним часом