1.4. Основні квантові логічні операції

У квантовому комп'ютері, як уже зазначалося, логічні операції проводяться в системі кубітів. Вони розбиваються на дискретну сукупність послідовних у часі базисних квантових логічних операцій - квантових вентилів (quantum gates). Кожен квантовий вентиль за фіксований проміжок часу виконує унітарне перетворення з виділеними кубітами. Квантовий вентиль здійснює оборотні операції і з цієї точки зору класичний оборотний комп'ютер є аналогом квантового комп'ютера. Одним з основних умов для побудови квантового комп'ютера є наявність універсального набору квантових вентилів, за допомогою якого може бути виконане будь унітарне перетворення в 2^L-вимірному гільбертовому просторі.

До однокубітових квантових операторів, діючих тільки на один кубіт, відносяться різні оператори повороту вектора стану кубіта в двомірному гільбертовому просторі. Це, зокрема, такі вентилі, як NOT, що описується матрицею 2x2 або оператором Паулі

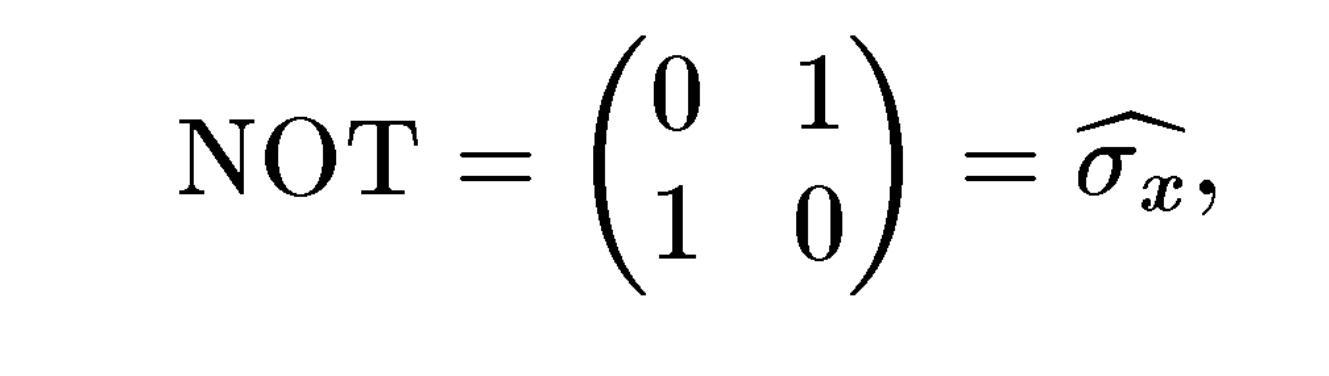
оператор Адамара (М. Наdamard), який здійснює самостійно (self snverse) операцію формування суперпозиції станів

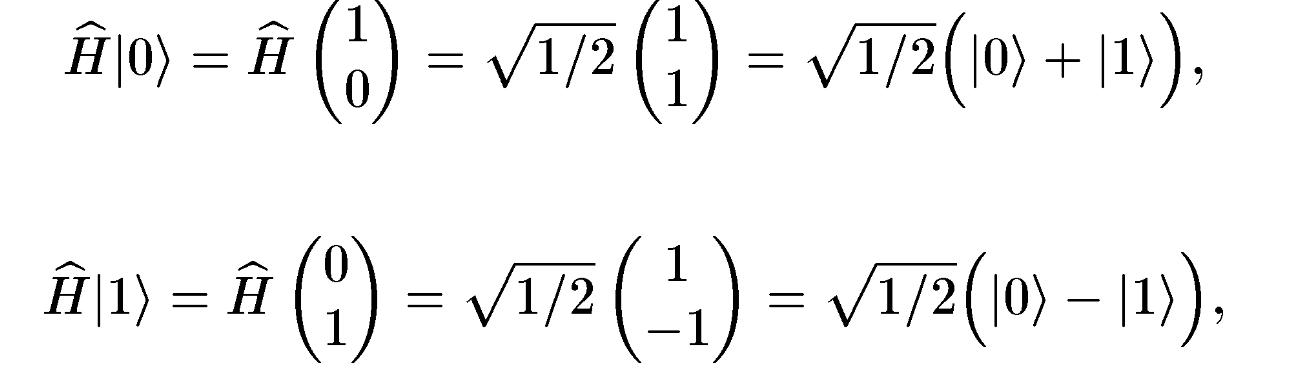
яку можна записати також у вигляді

Оператор Адамара Н описується матрицею

Аналогічне перетворення в системі L кубітів здійснюється за допомогою N=2^L-мірного оператора Уолша-Адамара (Walsh-Hadamald), що представляє собою прямий добуток однокубітових операторів Адамара:

Використовуючи вираз (2.3), для нього отримаємо

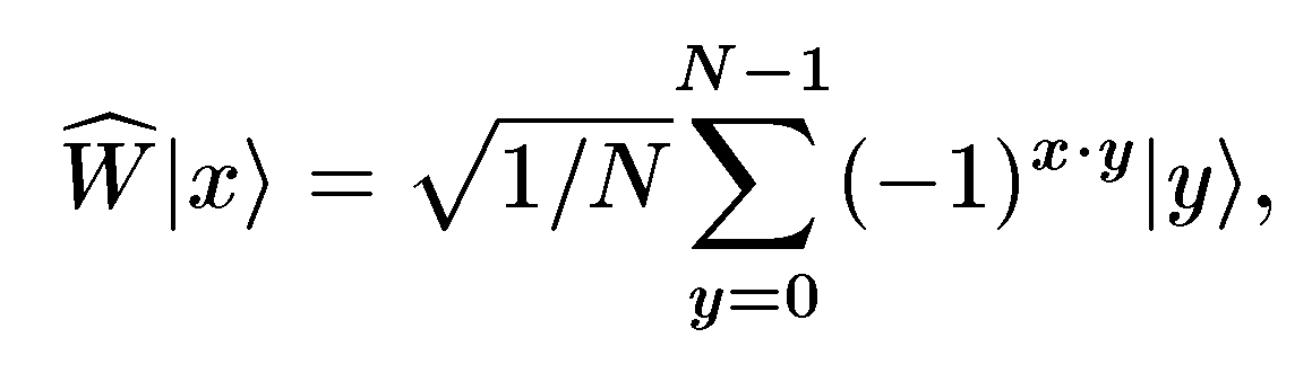
де х, у являють собою ланцюжки з N=2^L станів L кубітів, а х • у означає їх побітовий скалярний добуток по модулю 2, яке визначається як . Існують і інші передставлення оператора W.

Двохкубітові вентилі відповідають операціям повороту в гільбертовому просторі двох взаємодіючих кубітів, які не можуть бути представлені у вигляді прямого добутку незалежних однокубітових операцій. Основним двохкубітовим вентилем є оборотний контрольований інвертор або оператор контрольований НЕ (СNOT), який у сукупності з відносно простими однокубітовими операціями може бути базовим для формування будь-якої унітарної операції в системі з понад двох кубітів [2.1].

Цей вентиль описується квантовою схемою і матрицею 4x4 наступного виду:

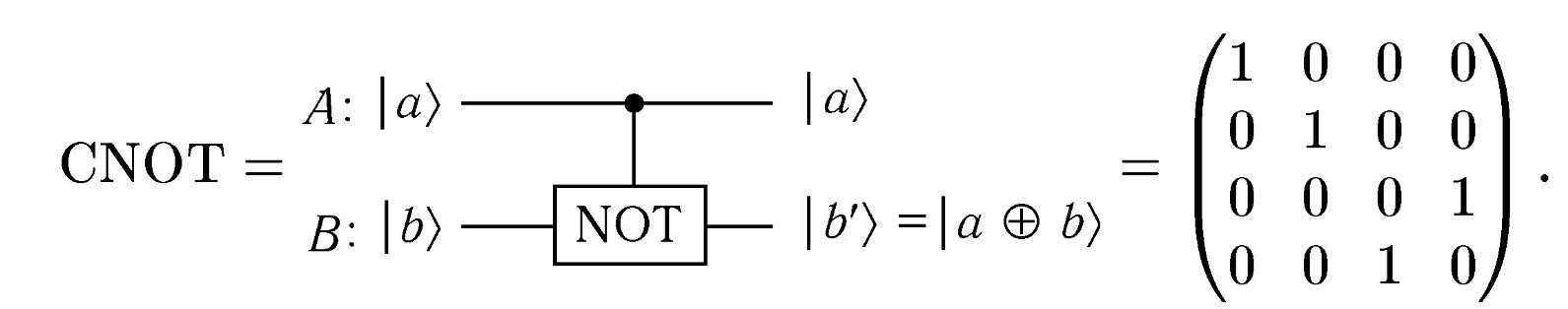
Послідовність операцій у квантових схемах прийнято розглядати зліва направо у відповідності з напрямком часу по горизонтальних лініях на схемі. Вентиль із симетричною щодо входу і виходу схемою описується симетричною матрицею. Перший кубіт А в операції СNOT є контролюючим, а другий B контрольованим, над ним і здійснюється операція NOT, за умови, якщо перший кубіт знаходиться в стані |1).

Зауважимо, що за допомогою СNOT можна здійснювати операцію копіювання або неруйнуючий вимір стану контролюючого кубіта, оскільки, вважаючи |b) = 0, отримаємо |b ') = |а).

У свою чергу оператор СNOT формально може бути побудований з трьох простіших вентилів [2.1-2.3]:

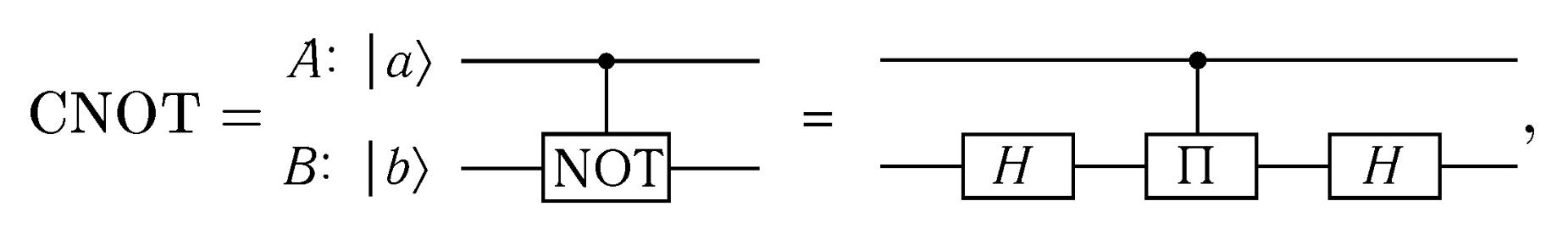
де

двохкубытовий оператор контрольованої зміни фази, що виробляє в розглянутому випадку зсув фази тільки стану | 1,1) на ПІ: (| 1,1) => -11,1)), залишаючи інші стани без змін. Для його виконання суттєва наявність фізичної взаємодії між кубітами.

Двохкубиіовий оператор обміну станами кубітів SWAP можна зіставити квантовою схемою, у якій послідовно виконуються три операції СNOT:

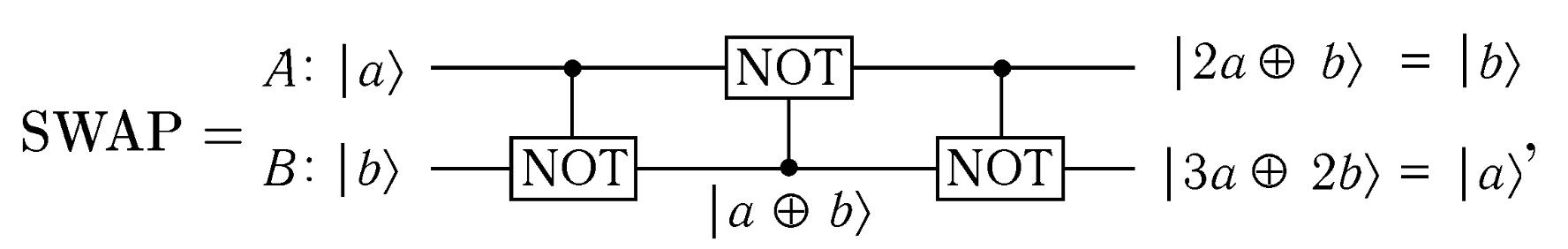
описувані матрицею

Зауважимо, що випадку коли стан | а) = | 0), третій оператор СNOT виявляється зайвим.

Операцію СNOT можна здійснити також за допомогою послідовності операцій наступного виду [2.4]:

де

- однокубітові операції повороту оператора спина що представляє стан кубіта, на кут ± ПІ / 2 навколо осі z: у спіновому просторі, а двохкубітові операції описуються матрицями

Використовуючи систему з трьох пов'язаних спінів-кубітів, можна сформувати і такий універсальний елемент, як вентиль Тоффолі або CCNOT [2.3]:

У цьому операторі керуючими є два кубіта А і В і один керований С. Він описується наступною матрицею 8x8 в базисних станах | 0,0,0), | 0,0,1), | 0,1,0), |1,0 , 0), | 0,1,1), |1,0,1), |1,1,0) і |1,1,1):

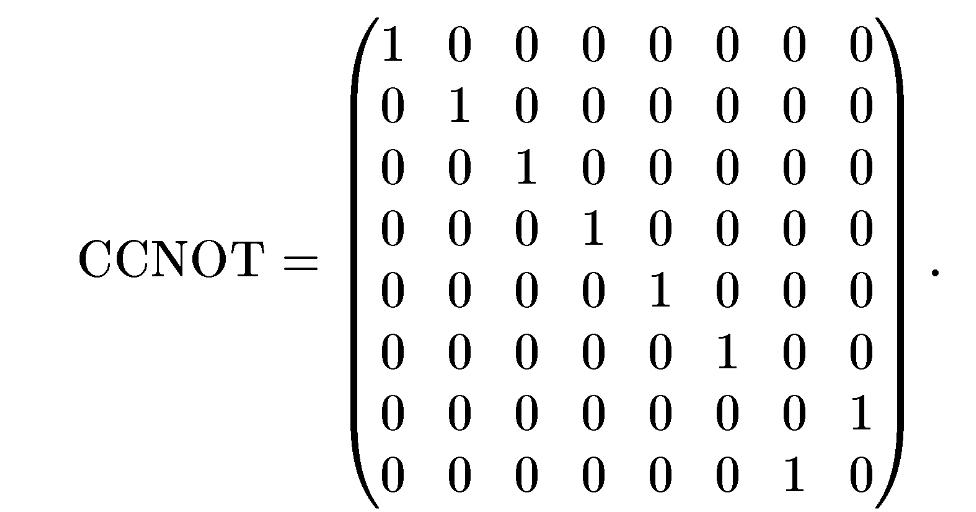
Така операція може бути виконана за допомогою п'яти двокубітових операцій [2.1].