6. Индексы структурных сдвигов
При изучении динамики качественных показателей приходится определять изменение средней величины индексируемого показателя, которое обусловлено взаимодействием двух факторов - изменением значения индексируемого показателя у отдельных групп единиц и изменением структуры явления. Под изменением структуры явления понимается изменение доли отдельных групп единиц совокупности в общей их численности. Так, средняя заработная плата на предприятии может вырасти в результате роста оплаты труда работников или увеличения доли высокооплачиваемых сотрудников. Так как на изменение среднего значения показателя оказывают воздействие два фактора, возникает задача определить степень влияния каждого из факторов на общую динамику средней.
Эта задача решается с помощью индексного метода, т.е. путем построения системы взаимосвязанных индексов, в которую включаются три индекса: переменного состава, постоянного состава и структурных сдвигов.
Индексом переменного состава называется индекс, выражающий соотношение средних уровней изучаемого явления, относящихся к разным периодам времени.
Например, индекс переменного состава себестоимости продукции одного и того же вида:
Индекс переменного состава отражает изменение не только индексируемой величины (в данном случае себестоимости), но и структуры совокупности (весов).
Общая формула индекса переменного состава:
,
где - индексируемые величины;
- веса индекса.
Индекс постоянного (фиксированного) состава - это индекс, исчисленный с весами, зафиксированными на уровне одного какого-либо периода, и показывающий изменение только индексируемой величины.
Индекс фиксированного состава определяется как агрегатный индекс. Так, индекс фиксированного состава себестоимости продукции рассчитывают по формуле:
Общая формула индекса постоянного состава:
Под индексом структурных сдвигов понимают индекс, характеризующий влияние изменения структуры изучаемого явления на динамику среднего уровня этого явления. Индекс определяется по формуле (при изучении изменения среднего уровня себестоимости):
Общая формула индекса структурных сдвигов:
Система взаимосвязанных
индексов при анализе динамики средней
себестоимости
имеет следующий
вид:
Индексы пространственно-территориального сопоставления
В статистической практике часто возникает потребность в сопоставлении уровней экономического явления в пространстве: по странам, экономическим районам, областям, т.е. в исчислении территориальных индексов. При построении территориальных индексов приходится решать вопрос, какие веса использовать при их исчислении. Например, если стоит задача сравнить цены двух регионов (А и Б), то можно построить два индекса:
и 
,
где
- индекс, в котором
в качестве базы сравнения применяются
данные по региону А;
- индекс, используемый
в качестве
базы сравнения данных
по региону Б.
Эти формулы могут дать совершенно различное представление о соотношении уровней явления. Например, при расчете по первой формуле значение признака будет ниже в регионе А, а по второй формуле - в регионе Б.
Пример.
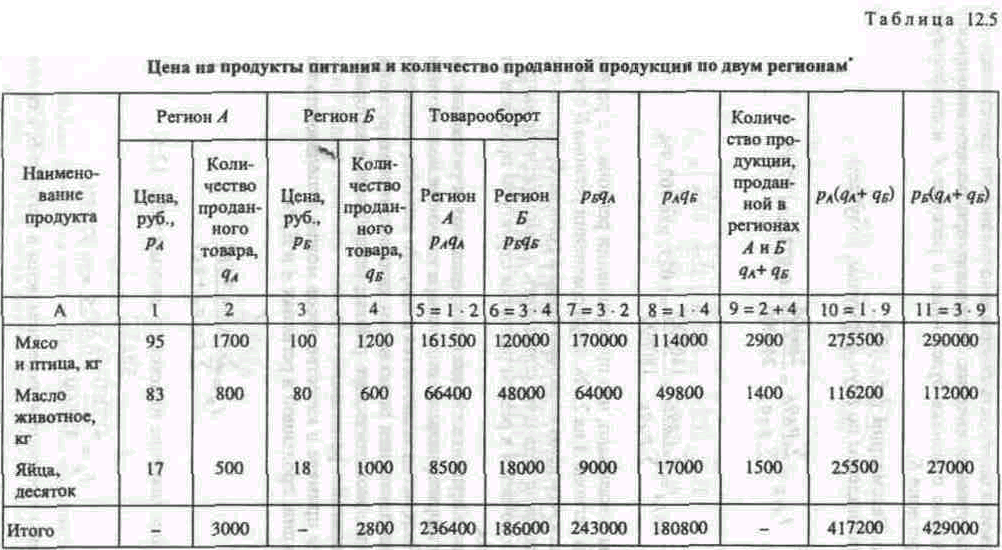
Рассчитав индексы по двум формулам, получаем:
Индексы показывают, что при сравнении региона А с регионом Б цены ниже в регионе А на 2,7%, а при сравнении региона Б с регионом А оказывается, что цены несколько выше в регионе Б. Таким образом, расчет индексов не позволяет определить, в каком регионе выше цены. Причина заключается в резком различии структуры продаж в отдельных регионах.
В статистике предлагаются различные методы построения территориальных индексов, в том числе метод стандартных весов. Этот метод заключается в том, что значения индексируемой величины взвешиваются не по весам какого-то одного региона, а по весам области, экономического района, республики, в которых находятся сравниваемые регионы.
В нашем примере в качестве весов можно использовать количество продукции, проданной в регионах А и Б, т.е.:
Определим значение индекса:
Цены в регионе А ниже, чем цены в регионе Б, в среднем на 2,75%.