2.4 Оцінка щільності та перевірка істотності статистичних взаємозв'язків

Оцінка впливу варіації факторної ознаки «х» на результативну «у» у методі аналітичного групування і лінійного рівняння регресії різна.

В аналітичному групуванні мірою щільності зв'язку є відношення міжгрупової дисперсії до загальної, яке називається кореляційним відношенням:

(2.5)

де – міжгрупова дисперсія, яка вимірює варіацію ознаки «у» під впливом фактора «х»;

– загальна дисперсія.

Міжгрупова та загальна дисперсії розраховуються за формулами:

(2.6)

(2.7)

Оцінимо щільність зв'язку між площею однокімнатних квартир і їх вартістю. Для цього необхідні розрахунки приведемо у таблицях 2.4 і 2.5.

Таблиця 2.4 – Розрахунок загальної дисперсії вартості реалізації однокімнатних квартир

Вартість квартир (уі)	8000	9000	10000	11000	12000	Разом
Кількість квартир (fi)	20	32	34	26	18	130
	9853
	– 1853	– 853	147	1147	2147	Х
	68672180	23283488	734706	34205834	82972962	209869170

Таблиця 2.5 – Розрахунок міжгрупової дисперсії вартості реалізації однокімнатних квартир

Площа квартир, м2	Кількість квартир (fi)
20-25	28	8571	9853	-1283	46090492
25-30	30	9367		-486	7085880
30-35	40	10225		372	5535360
35 і вище	32	11250		1397	62451488
Разом	130	9853		Х	121163220

Кореляційне відношення для нашого прикладу аналітичного групування:

Тобто 57,7% варіації ціни за однокімнатні квартири пояснюється варіацією площі реалізованих квартир. Або ціна однокімнатної квартири на 57,7% залежить від площі квартири.

Перевірка істотності взаємозв'язку в аналітичному групуванні проводиться шляхом порівняння фактичного значення з його критичним значенням для певного рівня суттєвості і числа ступенів свободи , де – число груп, – обсяг сукупності. Якщо > – то зв'язок вважається істотним.

Значення визначається за допомогою таблиці критичних значень кореляційного відношення і коефіцієнта детермінації R² при , яка наведена у додатку.

Для нашого прикладу критичне значення при дорівнюватиме .

Таким чином, розраховане фактичне значення значно перевищує критичне, а значить взаємозв'язок між факторами визнається істотним.

Оцінка щільності кореляційного зв'язку в лінійному рівнянні регресії проводиться з використанням коефіцієнта кореляції Пірсона:

(2.8)

Згідно до даних нашого прикладу про взаємозалежність видобутку вугілля від розміру інвестицій коефіцієнт кореляції становить:

Значення коефіцієнта кореляції коливається від -1 до 1. Чим ближче значення до одиниці, тим щільніший зв'язок. Коли зв'язок прямий, r – величина додатна, а коли зворотній – від'ємна. В нашому прикладі r додатна величина – зв'язок прямий, значення 0,8432 свідчить про вагомий вплив інвестицій на обсяг видобутку вугілля.

Перевірка істотності кореляційного зв'язку ґрунтується на порівнянні фактичного значення коефіцієнта детермінації R² з критичними, аналогічно до кореляційного відношення в аналітичному групуванні.

Коефіцієнт детермінації взаємопов’язаний з лінійним коефіцієнтом кореляції r. Коли зв'язок лінійний, , де – індекс кореляції. Коефіцієнт детермінації в нашому прикладі становить R²=0,71 (0,8432²), це означає що 71% варіації видобутку вугілля залежить від розміру інвестицій.. Критичне значення коефіцієнта детермінації визначається за тим же принципом, як і в аналітичному групуванні. Число ступенів свободи для певного рівня істотності , де – число параметрів в рівнянні регресії, – обсяг сукупності.

Таким чином, при коефіцієнт детермінації дорівнюватиме . Тобто, фактичне значення коефіцієнта детермінації значно перевищує його критичне (0,71>0,362), що з імовірністю 0,95 підтверджує істотність зв'язку між розміром інвестицій та видобутком вугілля.

Коефіцієнт детермінації, як міра щільності кореляційного зв'язку, використовується як при лінійних так і при нелінійних зв'язках. Розраховується за формулою:

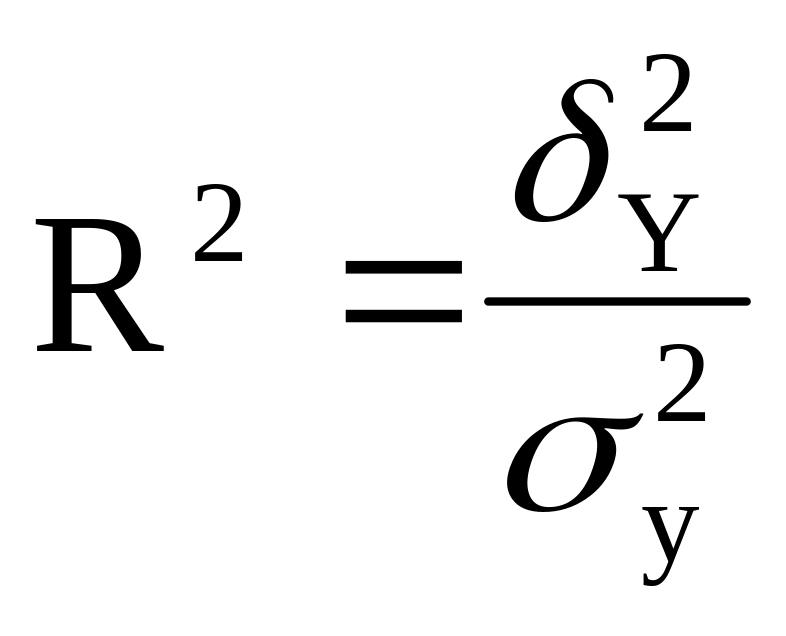(2.9)

де – факторна дисперсія;

– загальна дисперсія.

Факторна та загальна дисперсії розраховуються за формулами:

(2.10)

(2.11)

Розрахунок коефіцієнта детермінації за формулами 2.10 та 2.11 для оцінки щільності зв'язку між розміром інвестицій та обсягом видобутку вугілля, надав відомий вже результат R²=0,71.