Вправи до підрозділу «Властивості середньої арифметичної величини»

1. Якщо частоти ряду розподілення перетворити у частості чи зміниться середня величина?

Відповіді: а) так; б) ні; в) точна відповідь відсутня.

2. Якщо частоти всіх значень ознаки зменшити у п’ять разів, а значення ознаки залишити без змін, то середня: 1) збільшиться у п’ять разів; 2) зменшиться у п’ять разів; 3) не зміниться; 4) зміну середньої величини передбачити неможливо.

Відповіді: 1); 2); 3); 4).

3. Якщо всі індивідуальні значення ознаки зменшити у шість разів, а частоти збільшити у 2 рази, то середня: 1) збільшиться у два рази; 2) зменшиться у три рази; 3) зменшиться у шість разів; 4) зміну середньої величини передбачити неможливо.

Відповіді: 1); 2); 3); 4).

4. Якщо частоти середніх значень ознаки зменшити на 35 одиниць, то середня: 1) зменшиться на 35; 2) зменшиться у 35 разів; 3) не зміниться; 4) зміну середньої величини передбачити неможливо.

Відповіді: 1); 2); 3); 4).

5. Після впровадження раціональних запропонувань витрати часу на обробку деталі кожним робітником скоротилися у 2 рази, а кількість оброблених деталей кожним робітником збільшилася у 2 рази. Середні витрати часу на обробку однієї деталі: 1) не змінилися; 2) зменшилися у два рази; 3) збільшилися у два рази; 4) передбачити зміну середньої неможливо.

Відповіді: 1); 2); 3); 4).

6. Якщо всі індивідуальні значення ознаки збільшити у 3 рази, а частоту зменшити у три рази, то середня: 1) не зміниться; 2) зменшиться у три рази; 3) збільшиться у три рази; 4) передбачити зміну середньої неможливо.

Відповіді: 1); 2); 3); 4).

5 Ряди розподілу. Показники варіації

5.1 Мода і медіана

У статистиці в якості характерних, визначальних характеристик ознак використовують структурні середні – моду і медіану.

Мода – це величина ознаки, яка найбільш часто зустрічається у даній статистичній сукупності.

Медіана – це значення ознаки, яка поділяє упорядкований ряд на дві рівні частини.

При визначенні моди у дискретному ряду не потрібні ніякі формули: модою буде та варіанта ряду, яка має найбільшу частоту.

У неперервних рядах з рівними інтервалами мода визначається за наступною наближеною формулою:

, (5.1)

де x₀ – нижня межа модального інтервалу, тобто інтервалу який має найбільшу частоту;

d – довжина модального інтервалу;

f₁ – частота попереднього до модального інтервалу;

f₂ – частота модального інтервалу;

f₃ – частота інтервалу наступного за модальним.

В якості модального, тобто інтервалу який містить моду, приймається інтервал який має найбільшу частоту.

Приклад 5.1. У таблиці 5.1 надано розподілення дорослого чоловічого населення за розміром взуття.

Таблиця 5.1 – Розмір взуття дорослих чоловіків

Розмір	38	39	40	41	42	43 та більше	Разом
Кількість чоловіків, % до результату	6	12	23	28	21	10	100

Так як це дискретний ряд розподілу, то модою у даному ряду буде 41 розмір, тому що він зустрічається у найбільшої кількості чоловіків.

Приклад 5.2. У таблиці 5.2 зведені дані про розподіл малих виробничих підприємств за вартістю основних виробничих фондів у розрахунку на одне підприємство.

Таблиця 5.2 – Вартість основних виробничих фондів на малих підприємствах

М₀

Вартість основних виробничих фондів, тис. грн.	до 10	10-14	14-18	18-22	22 і більше	Разом
Кількість підприємств	10	22	34	28	6	100

F₁ F₂ F₃

Модальним (який містить моду) є інтервал 14-18 тис. грн. Значення моди визначимо за формулою 5.1.

Медіаною – у варіаційному ряду є значення ознаки у той одиниці сукупності, яка поділяє варіаційний ряд за сумою частот на дві рівні частини, так, що у одній половині одиниць значення ознаки менше медіани, а у другій – більше її.

Найбільш часто медіану визначають за даними інтервального варіаційного ряду. Це пояснюється тим, що при невеликій кількості дискретних значень варіантів, значення ознаки рівне медіані можуть мати більшість одиниць сукупності, що робить медіану у даному випадку непоказовою.

В інтервальному варіаційному ряді медіана визначається у наступній послідовності: спочатку визначається інтервал, у межах якого розташована медіана, потім за формулою розраховується конкретне значення медіани.

Для визначення медіанного інтервалу підраховується сума накопичених частот до тієї межі, поки не будуть отримані дві суміжні величини накоплених частот, одна з яких менше, а друга більше половини суми всіх частот ряду. Тоді медіана знаходиться у межах того інтервалу, складання частоти якого до першої суми дає другу.

Розрахунок конкретного значення медіани проводиться за формулою:

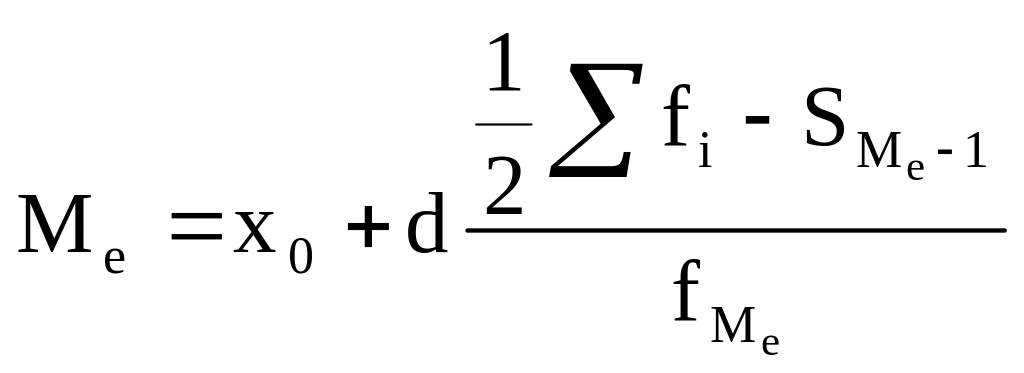, (5.2)

де х₀ – нижня межа медіанного інтервалу;

d – довжина медіанного інтервалу;

∑f_i – сума частот ряду;

S_Me-1 – сума накопичених частот попереднього до медіанного інтервалу;

f_Me – частота медіанного інтервалу.

Приклад 5.3. Розподілення заводів за кількістю цементу, який ними виробляється надано варіаційним рядом у графах 1-2 таблиці 5.3.

Необхідно визначити медіану виробництва цементу.

Таблиця 5.3 – Виробництво цементу заводами

Групи заводів за кількістю цементу, який ними виробляється, тис. т.	Кількість заводів, % до підсумку	Накопичені частоти
1	2	3
до 250	12	12
250-275	18	30<50
275-300	22	52>50
300-325	28	80
325-350	10	90
350-375	8	98
375 і більше	2	100
Разом	100	––

Обсяг ряду дорівнює ∑f=100, половина суми ½ ∑f_i=50. Підрахував суму накопичених частот (гр. 3 табл. 5.3) знаходимо, що медіана лежить в інтервалі 275-300 тис. т. (сума накопичених частот до цього інтервалу менша половини всього обсягу ряду, а з частотою цього інтервалу – більша). З цього можна визначити і значення медіани:

х₀=275; d=25; S_Me-1=30; f._Me=22:

тис. грн.

У підрозділі 5.2 наведені приклади задач, які рекомендуються студентам для самостійного рішення з метою закріплення знань з теми підрозділу 5.1 «Мода і медіана».