4 Середні величини

Середні величини – це показники, які виражають типові розміри кількісних ознак, що варіюють, якісно однорідних статистичних сукупностей. При розрахунку середньої величини вплив відхилень індивідуальних значень ознаки у окремих елементів статистичної сукупності взаємно компенсується, а розмір ознаки обумовлений загальними для даної групи причинами, навпаки, проявляється.

Обчислюючи середню величину слід прийняти до уваги, що вона буде дійсною типовою величиною при дотриманні наступних неодмінних умов:

1) ознака повинна бути суттєвою. Якщо обрати для аналізу несуттєву ознаку, тоді розрахована середня величина буде маловажною;

2) середня величина повинна розраховуватися для груп сукупності, які об’єднані якісною однорідністю. У протилежному випадку, можна викривити дійсні риси ознаки. У зв’язку з цим існує наявний взаємозв’язок між методом середніх величин і методом статистичного групування, який дозволяє попередньо відокремити якісно однорідні групи;

3) сукупність одиниць, для яких знаходиться середня повинна бути достатньо великою. При невеликій чисельності випадкові, індивідуальні обставини здатні викривити результати та стати перепоною у виявленні загальних закономірностей.

Приступаючи до обчислення середніх величин, необхідно прийняти до уваги, що середня величина повинна розраховуватися з врахуванням економічного змісту показника, який визначається, та відображає його природу.

Приклад 4.1.

=

=

=

=

Такий підхід дозволяє правильно визначити середню величину ознаки та обрати форму середньої.

4.1 Середня арифметична та середня гармонічна

Існують різні види середніх величин. Найбільш часто у розрахунках використовується середня арифметична, середня гармонічна, середня геометрична та середня квадратична. Вони називаються ступеневими середніми.

Ступенева середня може бути у двох видах: незважена (проста) та зважена.

Якщо варіанти у сукупності не повторюватимуться, або зустрічаються по однаковому числу разів, тобто можна сказати, «мають однакову вагу», тоді у цьому випадку використовується незважена (проста) середня арифметична.

Приклад 4.2. У таблиці 4.1 наведені наступні дані про вік п’яти робітників фарбувального цеху ткацької фабрики.

Таблиця 4.1 –Вік робітників фарбувального цеху

Вік робітників, роки

22

24

32

35

42

Необхідно визначити середній вік робітників.

Для визначення середнього віку цієї групи робітників достатньо знайти суму їх віку та поділити на число робітників, тобто:

(4.1)

Аналогічно простим буде розрахунок, якщо число робітників у кожній віковій групі буде однаковим.

Приклад 4.3. У таблиці 4.2 наведені дані про вік двадцяти п’яти робітників фарбувального цеху ткацької фабрики.

Необхідно також визначити середній вік робітників.

Таблиця 4.2 –Вік робітників фарбувального цеху

Вік робітників, роки	22	24		32		35	42
Число робітників у групі	5	5	5		5		5

Розрахунок слід проводити за тим правилом, що вказано вище.

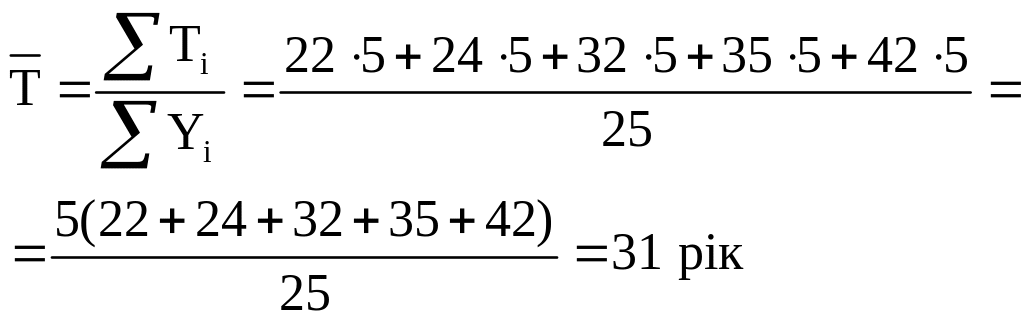(4.1)

У наведених прикладах достатньо використовувати формулу середньої арифметичної простої: у першому випадку значення варіант не повторюється, у другому – повторюється однакову кількість разів.

Якщо сукупність, яка досліджується роздроблена на окремі групи, які відрізняються не тільки за величиною осередняємої ознаки, але і за числом одиниць, які містяться у кожній з груп, тоді у цьому випадку використовують середню арифметичну зважену.

Приклад 4.4. Місячна заробітна плата 10 робітників характеризується наступними даними, які наведені у таблиці 4.3.

Таблиця 4.3 – Місячна заробітна плата 10 робітників

Номер групи	Заробітна плата, грн.	Число робітників, осіб
1	Х1=200	F1=2
2	Х2=350	F2=5
3	Х3=550	F3=3

Необхідно розрахувати середню місячну заробітну плату одного робітника.

Середню заробітну плату можна виразити логічною формулою:

=

Використовуючи літерні позначення, які вказані у таблиці, цю середню можна представити наступним чином:

(4.2)

Формула 4.2 і є формулою зваженої середньої арифметичної. Добуток і т. д. є варіанти, які помножені на їх ваги та називаються зваженими варіантами. Таким чином зважена середня арифметична дорівнює сумі зважених варіант, яка поділена на суму важелів.

У нашому прикладі вона дорівнює:

Зважену середню арифметичну також застосовують при обчисленні загальної середньої з часткових групових середніх. Наприклад, при визначенні середньої заробітної робітників заводу, якщо відома середня заробітна плата і число робітників кожного цеху.

Слід мати на увазі, що у випадку кожної конкретної задачі співмножники “x” і “f”, а також добуток “xf” мають певний економічний зміст. Так у прикладі 4.4 обчислення середньої заробітної плати:

х_і – заробітна плата окремих груп робочих (варіанти);

f_i – число робочих у окремих групах (важелі);

х_іf_i – фонд заробітної плати окремих груп робочих;

– фонд заробітної плати усієї сукупності робітників.

Розрахунок середніх за даними інтервальних варіаційних рядів проводиться наступним чином: у кожній групі (інтервалі групувальної ознаки) за величину конкретної варіанти умовно приймається середина інтервалу, тобто проста середня арифметична з двох крайніх значень інтервалу. Наступні розрахунки подібні до наведених вище.

Приклад 4.5. Дана група заводів, які виробляють однакові вироби, а також відомі дані про витрати на 1 грн. товарної продукції кожною групою заводів (див. табл. 4.3).

Необхідно визначити середні витрати на 1 грн. товарної продукції всіма заводам.

Таблиця 4.3 – Витрати на 1 грн. товарної продукції кожною групою заводів

Витрати на 1 грн. товарної продукції	Число заводів	Загальний обсяг товарної продукції, який вироблено всіма заводами, тис. грн.
70-75	2	200
75-80	4	300
80-85	8	350
85-90	11	450
90-95	5	100

Витрати на 1 грн. товарної продукції можна виразити логічною формулою:

=

Використовуючи вихідні дані прикладу 4.5 та дотримуючись вищенаведеної логіко-математичній формули складемо розрахункову таблицю 4.4.

Таблиця 4.4 – Розрахункова таблиця до розрахунків прикладу 4.5

Умова			Рішення
Групи заводів за рівнем витрат на 1 грн. товарної продукції, коп.	Число заводів	Загальний обсяг продукції, який вироблено усіма заводами, тис. грн.	Середній рівень витрат на 1 грн. товарної продукції у групі, коп.	Загальна сума витрат на виробництво всієї продукції, тис. грн.
70-75	2	200		x1f1=145
75-80	4	300		x2f2=232,5
80-85	8	350		x3f3=288,75
85-90	11	450		x4f4=393,75
90-95	5	100		x5f5=92,5
Разом	30	1400	–––	1152,5

Застосовуючи формулу зваженої середньої арифметичної, отримаємо:

Звичайно, слід розуміти, що величина отриманої середньої внаслідок припущенних умовностей не є достатньо точною, а лише наближеною, однак практика виправдовує такий розрахунок.

Розрахунок за формулою середньої арифметичної, при певних умовах конкретної задачі не завжди виправдано. Отримана при цьому середня може не бути загальною характеристикою осередненої ознаки у наданій задачею сукупності.

Приклад 4.6 Валовий збір зерна пшениці у кожному з двох відділень сільгосппідприємств склав 240ц. Врожайність у першому відділені 24ц. з гектару, а у другому 30 ц. з гектару. Слід визначити середню врожайність пшениці на сільгосппідприємстві.

На перший погляд рішення задачі достатньо просте – використати формулу середньої арифметичної простої:

Перевіримо рішення. По сутті середня врожайність визначається за формулою:

=

Тоді,

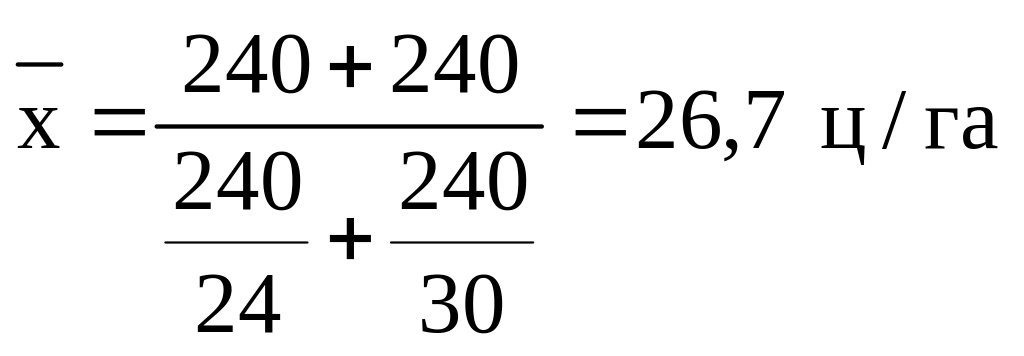
Як видно середня арифметична у випадку даної задачі не підходить (середня арифметична складає 27 ц/га, а фактична середня врожайність тільки 26,7 ц/га). Слід звернути увагу, що у задачі яка розглядається, відомі конкретні значення ознаки (варіанти врожайності – х_і) і обсяг явища (валовий збір зерна пшениці – w_i), який представляє перемноження варіантів на їх ваги (одиниці посівної площі – f_i) w_i=x_if_i.

Якщо використовувати формулу середньої арифметичної, тоді попередньо слід виокремити «ваги» (f_i), як частку від поділення (f_i= ), після цього розрахунок виглядатиме звично, як для середньої арифметичної – , але якщо прийняти до уваги, що x_if_i= w_i, а f_i= отримаємо формулу:

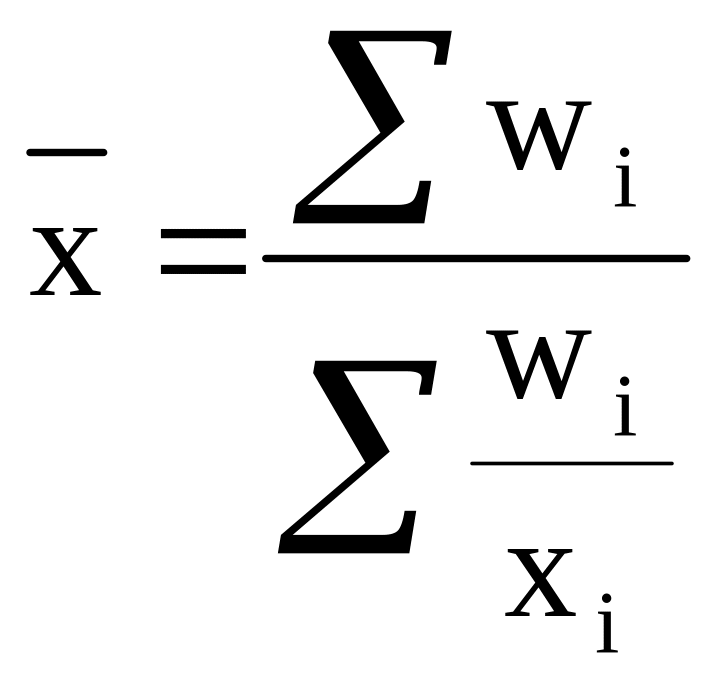, (4.3)

Формула 4.3 і є формулою середньої гармонічної зваженої.

Якщо w₁=w₂=w₃=…=w_n, то формула (4.3) прийме вид середньої гармонічної простої:

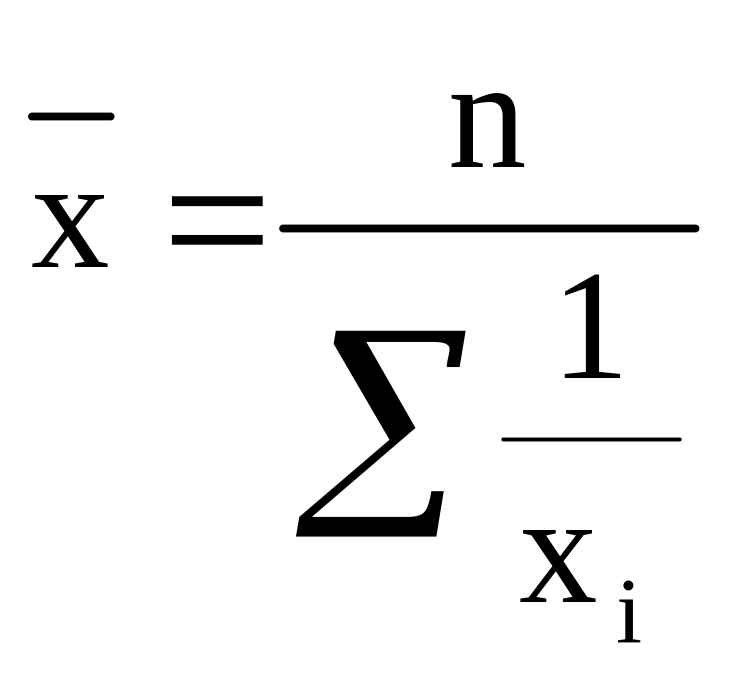, (4.4)

Дробі ; ; … у знаменнику формули 4.4 виражають числа зворотні заданим варіантам х₁; х₂; х₃…х_n. Назвемо ці числа зворотними варіантами. Тоді можна дати таке визначення: проста середня гармонічна утворюється шляхом поділення числа варіант (n) на суму зворотних варіант ( ). У випадку наведеного вище прикладі, коли w₁=w₂=240 га, отримаємо:

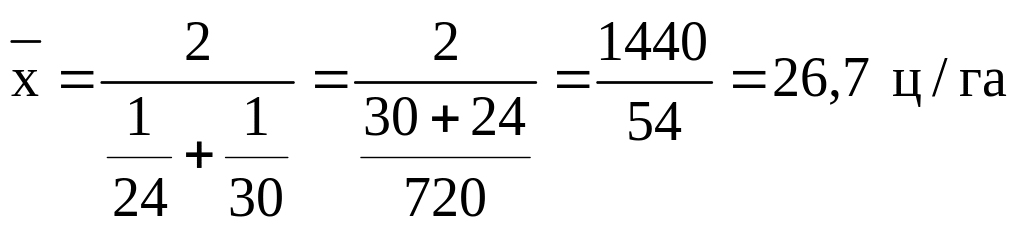
У наведеному прикладі варіантами є врожайність, а вагами – валовий збір зерна пшениці (однаковий для кожного відділення).

Ці ваги відрізняються від важелів середньої арифметичної. У середній арифметичній вагами (f_i) була сукупність (число) одиниць – носіїв ознаки, яка досліджується.

У задачі, яка розглядається, хоча одиницею – носієм ознаки, яка досліджується, все таки є посівна площа, однак ваги у цьому випадку (валовий збір зерна пшениці) представляють собою добуток варіант (врожайності) і одиниць – носіїв ознаки (посівної площі). Якщо ваги рівні, що має місце у прикладі, який розглядаємо, тоді у розрахунку використовується проста (незважена) середня гармонічна.

Якщо ваги різні, то застосовується зважена середня гармонічна, яка має наступний вид:

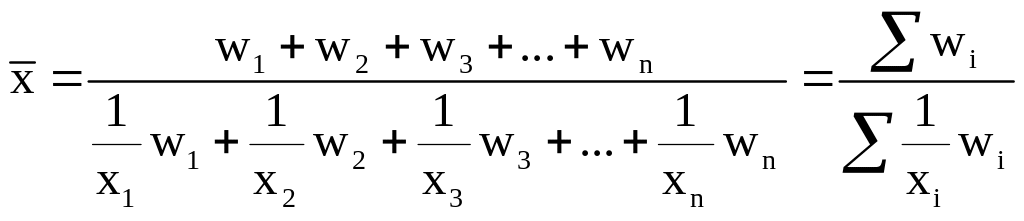, (4.5)

Тобто середня гармонічна зважена утворюється шляхом поділення суми важелів на суму зважених зворотних варіант.

Приклад 4.7. У таблиці 4.5 наведені дані по трьом автомобільним підприємствам.

Таблиця 4.5 – Дані по автомобільним підприємствам

Підприємство	Собівартість 1 т.км, коп.	Загальні витрати вантажообігу, тис. грн.
1 2 3	40,12 42,58 48,84	282,0 618,0 261,8

Необхідно визначити середню собівартість 1 т.км. по трьом підприємствам. Середню собівартість визначимо за наступною логічною формулою:

=

За умовою прикладу відомі загальні витрати по вантажообігу, які представляють собою добуток собівартості (s_i) 1 т. км. на величину пробігу автомобільного транспорту (l_i), тобто w_i=s_il_i. Загальний пробіг автомобільного транспорту можна визначити як частку від поділення , тоді розрахункова формула матиме вигляд:

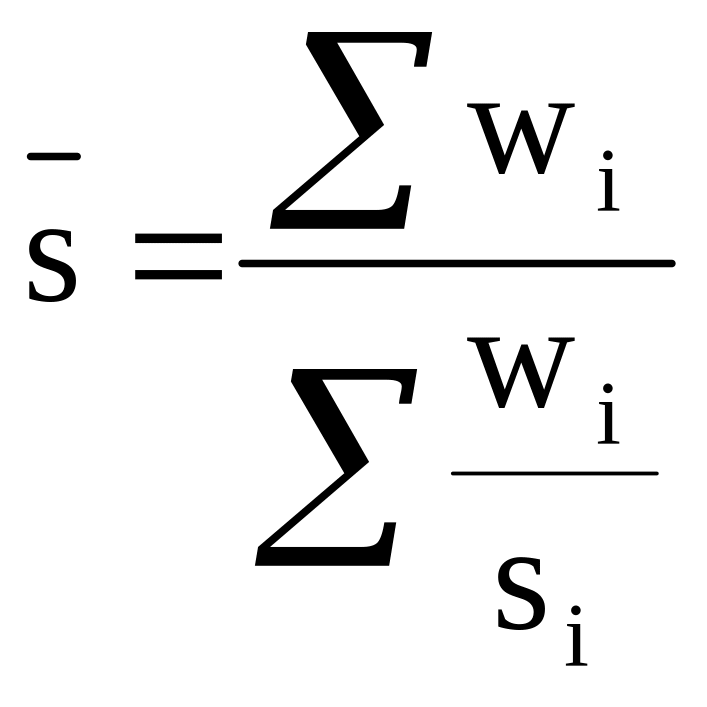, (4.6)

Це формула середньої гармонічної зваженої. Важелями (w_i) є загальні витрати по вантажообігу. Варіантами (s_i) – собівартість 1 т. км. по окремим автомобільним підприємствам. Підставляючи значення у формулу 4.6 отримаємо:

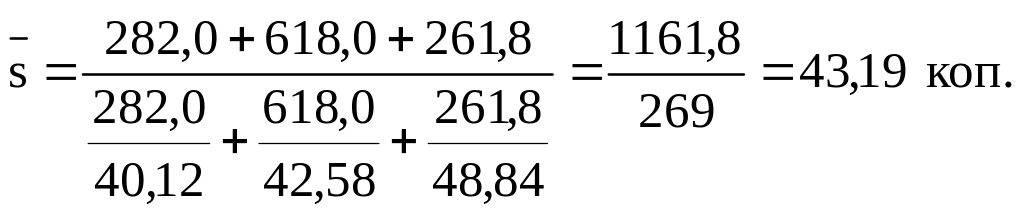
Приклад 4.8. У таблиці 4.6 наведені дані по фабриці «Схід» за I квартал поточного року.

Таблиця 4.6 – Дані про браковану продукцію на підприємстві за I квартал поточного року

Цех	Відсоток браку, %	Загальний обсяг бракованої продукції, грн.
1 2 3	1,6 0,8 1,2	580 720 850

Необхідно визначити середній відсоток браку по трьом цехам фабрики за I квартал.

Середній відсоток браку визначається логічною формулою:

=

Чисельник формули задано умовою задачі, а знаменник визначається за формулою:

=

Тоді:

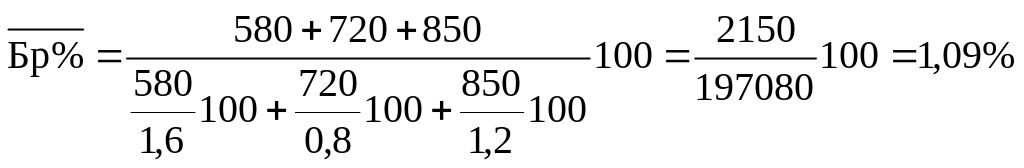
Важелем у даній задачі буде обсяг бракованої продукції.