
- •Авторегрессионная модель
- •Операторное представление
- •Автокорреляционная функция
- •Оценка параметров модели
- •Сезонные модели авторегрессии
- •Последствия автокорреляции
- •Обнаружение автокорреляции
- •Тесты на обнаружение автокорреляции Критерий Дарбина-Уотсона
- •Методы устранения автокорреляции Автокорреляция как следствие неправильной спецификации модели
- •Методы авторегрессионных преобразований первого порядка
Методы устранения автокорреляции Автокорреляция как следствие неправильной спецификации модели
В силу ряда причин в регрессионных моделях может иметь место корреляционная зависимость между соседними случайными отклонениями. Это нарушает одну из фундаментальных предпосылок МНК. Вследствие этого оценки, полученные на основе МНК, перестают быть эффективными. Это делает ненадёжными выводы по значимости коэффициентов регрессии и по качеству самого уравнения. Поэтому достаточно важным является умение не только определять наличие автокорреляции, но и умение устранять это нежелательное явление.
При установлении автокорреляции необходимо в первую очередь проанализировать правильность спецификации модели. Возможно, автокорреляция вызвана отсутствием в модели некоторой важной объясняющей переменной. Следует попытаться определить данный фактор и учесть его в уравнении регрессии. Можно также попытаться изменить формулу зависимости (например, линейную заменить на гиперболическую или лог-линейную).
Если после ряда возможных усовершенствований регрессии автокорреляция по-прежнему имеет место, то, возможно, это связано с внутренними свойствами ряда отклонений t. В этом случае возможны определенные преобразования, устраняющие автокорреляцию
Методы авторегрессионных преобразований первого порядка
Наиболее распространенным приёмом устранения автокорреляции является подбор соответствующего преобразования модели. В линейных моделях наиболее простым преобразованием является авторегрессионное преобразование первого порядка AR(1).
Для простоты рассмотрим модель парной линейной регрессии
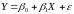 (8.30)
(8.30)
Тогда наблюдениям t и t–1 соответствуют формулы:
 ,
(8.31)
,
(8.31)
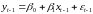 .
(8.32)
.
(8.32)
Пусть случайные отклонения подвержены воздействию авторегрессии первого порядка:
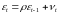 ,
(8.33)
,
(8.33)
где
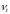 – случайные отклонения, удовлетворяющие
всем условиям Гаусса-Маркова, а коэффициент
известен. Вычтем из (8.31) соотношение
(8.32), умножение на :
– случайные отклонения, удовлетворяющие
всем условиям Гаусса-Маркова, а коэффициент
известен. Вычтем из (8.31) соотношение
(8.32), умножение на :
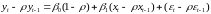 .
(8.34)
.
(8.34)
Положим
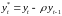 ,
,
 ,
,
 ,
и с учётом (8.33) получим:
,
и с учётом (8.33) получим:
 ,
(8.35)
,
(8.35)
Так
как по предположению коэффициент
известен, то очевидно,
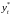 ,
,
 ,
вычисляются достаточно просто. В силу
того, что случайные отклонения t
удовлетворяют предпосылкам МНК, оценки
,
вычисляются достаточно просто. В силу
того, что случайные отклонения t
удовлетворяют предпосылкам МНК, оценки
 и
и
 будут обладать свойствами наилучших
несмещенных оценок (BLUE-оценками).
будут обладать свойствами наилучших
несмещенных оценок (BLUE-оценками).
Преобразование (8.34) называется авторегрессионным преобразованием (или преобразованием Бокса-Дженнинга).
Однако
остается одна небольшая проблема. Если
в выборке нет данных, предшествующих
первому наблюдению, то мы не сможем
вычислить
 и
и
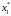 и потеряем первое наблюдение. Число
степеней свободы уменьшится на единицу
и это вызовет потерю эффективности,
которая может в небольших выборках
перевесить повышение эффективности от
устранения автокорреляции.
и потеряем первое наблюдение. Число
степеней свободы уменьшится на единицу
и это вызовет потерю эффективности,
которая может в небольших выборках
перевесить повышение эффективности от
устранения автокорреляции.
Эту проблему, к счастью, можно довольно легко обойти, пользуясь поправкой Прайса-Уинстона:

 ,
,
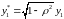 .
(8.36)
.
(8.36)
Отметим, что авторегрессионное преобразование может быть обобщено на произвольное число объясняющих переменных, т.е. использовано для уравнения множественной регрессии. Кроме того, авторегрессионное преобразование первого порядка может быть обобщено на преобразования и более высоких порядков.
На практике значение , как правило, неизвестно и его необходимо оценивать. Существует несколько способов его оценивания. Приведем некоторые из них.
Самый простой способ определения основан на статистике Дарбина-Уотсона. Напомним, что DW-статистика тесно связана с коэффициентом автокорреляции 1-го порядка:
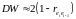 .
.
В
качестве оценки
можно взять коэффициент
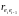 .
Отсюда получим
.
Отсюда получим
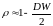 .
(8.37)
.
(8.37)
Этот способ оценивания весьма неплох при большом числе наблюдений. В этом случае оценка параметра будет достаточно точной.
Более точные оценки получаются при использовании МНК. Рассмотрим две процедуры, которые часто реализуются в компьютерных программах.
Рассмотрим метод Кохрэна-Оркатта. Алгоритм этого метода носит итеративный характер. Опишем его на примере парной регрессии
(8.38)
и авторегрессионной схемы первого порядка
. (8.39)
1) Обычным МНК оценивается регрессия (8.38) и для неё определяются оценки et отклонений t.
2) Обычным МНК оценивается авторегрессионное уравнение (8.39):
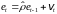 ,
(8.40)
,
(8.40)
где
 – оценка коэффициента .
– оценка коэффициента .
3) На основе данной оценки строится новое уравнение
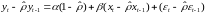 ,
(8.41)
,
(8.41)
с помощью которого оцениваются коэффициенты и (в этом случае значение известно).
4)
Значения
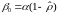 и
и
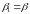 подставляются в (8.38). Вновь вычисляются
оценки et
отклонений и процесс возвращается к
этапу 2.
подставляются в (8.38). Вновь вычисляются
оценки et
отклонений и процесс возвращается к
этапу 2.
Чередование этапов осуществляется до тех пор, пока не будет достигнута требуемая точность, т.е. пока разность между предыдущей и последующей оценками не станет меньше любого наперед заданного числа.
Другой способ оценки – метод Хилдрета-Лу. Эта процедура, также широко применяемая в регрессионных пакетах, основана на тех же самых принципах, но использует другой алгоритм вычислений.
1) Преобразованное уравнение регрессии (8.41) для каждого значения из интервала (–1; 1) с заданным шагом внутри его (например, 0,001; 0,01 и т.д.).
2) Выбирают то значения , для которого сумма квадратов отклонений в преобразованном уравнении минимальна. Значения и 1 оцениваются из уравнения (8.41) именно с данным значением .
СПИСОК ЛИТЕРАТУРЫ
Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс.
Носко В.П. Эконометрика. Введение в регрессионный анализ временных рядов
Айвазян С. А. Прикладная статистика. Основы эконометрики. Том 2.
Доугерти К. Введение в эконометрику: Пер. с англ.
Кремер Н. Ш., Путко Б. А. Эконометрика.
План.
Авторегрессионная модель.
Автокорреляция.
Суть и причины автокорреляции.
Последствия автокорреляции.
3)Методы устранения автокорреляции.
3.Авторегрессионное преобразование.
