Обнаружение автокорреляции

В силу неизвестности значений параметров уравнения регрессии неизвестными будут также и истинные значения отклонений _t. Поэтому выводы об их независимости осуществляются на основе оценок e_t, полученных из эмпирического уравнения регрессии.

Самый простой и наглядный способ определения автокорреляции является графический. Существует несколько вариантов графического определения автокорреляции.

О дин из них, увязывающий отклонения e_t с моментами t их получения (или их порядковыми номерами i), приведён на рис. 8.7. Это т.н. последовательно-временные графики. В этом случае по оси абсцисс обычно откладываются либо время (момент) получения статистических данных, либо порядковый номер наблюдения, а по оси ординат – оценки отклонений e_t.

Естественно предположить, что на рис. 8.7а-г имеются определенные связи между отклонениями, т.е. автокорреляция имеет место. Отсутствие зависимости на рис. 8.7д скорее всего свидетельствует об отсутствии автокорреляции.

Н апример, на рис. 8.7б отклонения вначале отрицательные, затем положительные, потом снова отрицательные. Это свидетельствует о наличии между отклонениями определённой зависимости. Более того, можно утверждать, что в этом случае имеет место положительная автокорреляция отклонений. Она становится весьма наглядной, если график 8.7б дополнить графиком зависимости e_t от e_t–1 (рис. 8.8).

Подавляющее число точек на этом графике расположено в I и III четвертях, подтверждая положительную зависимость между соседними отклонениями.

Тесты на обнаружение автокорреляции Критерий Дарбина-Уотсона

Наиболее известным критерием обнаружения автокорреляции первого порядка является критерий (тест) Дарбина-Уотсона. Этот простой критерий определяет наличие автокорреляции между соседними членами (автокорреляции первого порядка).

Критерий Дарбина-Уотсона (критерий DW) основан на простой идее: если корреляция случайных отклонений регрессии _i не равна нулю, то она присутствует и в остатках (оценках отклонений) регрессии e_i, получающихся в результате применения обычного МНК.

В критерии Дарбина-Уотсона проверяется некоррелированность не любых, а только соседних e_i. Соседними обычно считаются соседние по времени (при рассмотрении временных рядов) или по возрастанию объясняющей переменной X (в случае перекрестной выборки) значения e_i. Для этих величин несложно рассчитать коэффициент корреляции, называемый в этом случае коэффициентом автокорреляции первого порядка:

. (8.27)

Здесь учтено, что для всех t.

На практике дл анализа коррелированности отклонений вместо коэффициента автокорреляции используют тесно связанную с ним статистику DW, рассчитываемую по формуле

. (8.28)

Действительно

.

Тогда

. (8.29)

Таким образом,

и её значения могут указать на наличие или отсутствие автокорреляции первого порядка. Действительно, если (автокорреляция отсутствует), то

.

Если (положительная автокорреляция), то

.

Если (отрицательная автокорреляция), то

.

Критерий Дарбина-Уотсона имеет один существенный недостаток – распределение DW-статистики зависит не только от числа наблюдений, но и от значений объясняющих переменных X_j. Это означает, что критерий Дарбина-Уотсона, вообще говоря, не представляет собой статистический критерий, в том смысле, что нельзя указать точно критическую область, которая позволяла бы отвергнуть гипотезу об отсутствии корреляции, если бы оказалось, что в эту область попало наблюдаемое значение статистики DW.

Однако существуют два пороговых значения d_в и d_н, зависящие только от числа наблюдений, числа объясняющих переменных и уровня значимости, такие, что выполняются следующие условия.

Если фактически наблюдаемое значение DW:

а) 0<DW<d_н, то принимается альтернативная гипотеза о положительной автокорреляции;

б) 4–d_н<DW<4, то принимается альтернативная гипотеза об отрицательной автокорреляции;

в) d_в<DW<4–d_в, то гипотеза об отсутствии автокорреляции принимается (не отвергается);

г) d_н<DW<d_в или 4–d_в<DW<4–d_н, то гипотеза об отсутствии автокорреляции не может быть ни принята, ни отвергнута, вопрос остается открытым (область неопределённости критерия).

И зобразим результат Дарбина-Уотсона графически:

Значения пороговых значений d_в и d_н, находятся по таблицам для DW-статистики по заданным , n и m. Отметим, что при использовании компьютерных регрессионных пакетов значение статистики Дарбина-Уотсона привдится автоматически при оценивании модели МНК.

Не обращаясь к таблице критических точек Дарбина-Уотсона, можно пользоваться «грубым» правилом и считать, что автокорреляция остатков отсутствует, если 1,5<DW<2,5. Для более надежного вывода целесообразно все-таки обращаться к табличным значениям.

Отметим некоторые недостатки критерия Дарбина-Уотсона.

• Следует иметь в виду, что значения пороговых значений DW-статистики определены для объёмов выборки не менее 15, т.е. критерий Дарбина-Уотсона применим для достаточно больших выборок.

• Наличие зоны неопределенности, конечно, представляет определенные трудности при использовании критерия Дарбина-Уотсона. Её ширина может быть довольно значительной. Наличие зоны неопределённости связано с тем, что распределение DW-статистики зависит не только от числа наблюдений и числа объясняющих переменных, но и от значений объясняющих переменных.

• Критерий Дарбина-Уотсона применяетс лишь для тех моделей, которые содержат свободный член ₀.

• Критерий Дарбина-Уотсона выведен лишь для неслучайных объясняющих переменных. Поэтому, если в составе объясняющих переменных присутствуют, например, т.н. лаговые значения результирующей переменной, то он должен соответствующим образом модифицирован (см. тему «Динамические ряды»).

• Необходимо учитывать, что критерий Дарбина-Уотсона проверяет только наличие автокорреляции между регрессионными остатками в последовательных наблюдениях, т.е. автокорреляцию первого порядка. Например, если 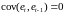, но , то с помощью критерия Дарбина-Уотсона не удастся обнаружить автокорреляцию.

Критерий Дарбина-Уотсона, безусловно является наиболее важным индикатором наличия автокорреляции. Однако, как выше было отмечено, он обладает и определенными недостатками. Поэтому наряду с этим критерием на практике применяются и другие критерии (тесты). Например, тест Бреуша-Годфри, тест ЛьюингаБокса и др.