2.6. Аналогия электрического поля в проводящей среде с электростатическим полем

По своей природе электростатическое поле и электрическое поле постоянных токов в проводящей среде различны. Однако, между соотношениями, характеризующими эти поля, можно провести формальную аналогию. Для удобства сопоставления выражений, относящихся к стационарному полю в проводящей среде и электростатическому полю в диэлектрике, представим их в виде табл. 2.1.

Таблица 2.1

Стационарное поле	Электростатическое поле
2	3

В пятой строке таблицы величина i есть ток сквозь сечение s трубки тока, а величина q есть заряд на поверхности заряженного тела в начале трубки электрического смещения сечением также s.

Сравнивая соотношения, относящиеся к стационарному полю и электростатическому полю, можно отметить, что они формально совпадут, если в последних заменить вектор электрического смещения вектором плотности тока , электрический заряд q – током i и абсолютную диэлектрическую проницаемость  - удельной проводимостью .

Оба поля также удовлетворяют уравнению Лапласа. Но если два поля удовлетворяют одному и тому же уравнению и в них выполняются граничные условия для сходных величин, то при одинаковой форме граничных поверхностей совокупность эквипотенциальных и силовых линий в этих двух полях будет одинаковой (то есть, картины поля будут совпадать).

На этом и основан так называемый метод электростатической аналогии, позволяющий в ряде случаев при расчете поля в проводящей среде воспользоваться готовыми решениями соответствующих задач электростатики (и наоборот).

В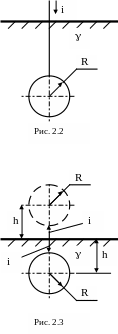 частности, формулы для электрической проводимости сред, в которых протекает ток, могут быть получены из соответствующих формул для емкости тел, так как в аналогичных задачах ток заменяется зарядом. Электрическая емкость тела или емкость между телами определяется геометрическими параметрами тел и абсолютными диэлектрическими проницаемостями сред, окружающих тела. Поэтому, чтобы получить формулу для проводимости G, достаточно заменить в соответствующей формуле для С абсолютные диэлектрические проницаемости  диэлектриков - удельными проводимостями  проводящих сред. Например, в однородных средах для аналогичных задач будет соблюдаться соотношение

2.7. Сопротивление заземления

Для осуществления соединения какой – либо точки электрической цепи с землей зарывают в землю металлические проводники, к которым присоединяют соответствующую точку цепи. Систему таких зарытых в землю проводников называют заземлителем. Электрический ток (при коротких замыканиях, при повреждении изоляции и т. д.), проходя через землю, встречает некоторое сопротивление, называемое сопротивлением заземления. По существу, это – сопротивление земли, которое встречает ток при растекании от заземлителя. Вдоль поверхности земли создается падение напряжения, которое вблизи от мест заземления может достигать опасных для жизни человека значений уже на длине шага человека. Поэтому весьма важно уметь рассчитывать сопротивление растеканию тока в земле при различных конструкциях заземлителей.

Формулы для электрической проводимости заземления могут быть написаны на основании метода электростатической аналогии по имеющимся формулам для емкости соответственно расположенных тел.

Рассмотрим некоторые примеры. Так как емкость уединенного шара радиуса R определяется по формуле (1.19), то проводимость заземления для шарового электрода, погруженного в землю столь глубоко, что можно пренебречь влиянием поверхности земли (рис. 2.2), должна быть равна

G = 4R.

Сопротивление заземления определяется как обратная величина проводимости

.

Если электрод расположен близко от поверхности земли (рис. 2.3), то в этом случае для расчета сопротивления заземления необходимо воспользоваться методом зеркальных изображений. Для этого необходимо отобразить реальный электрод относительно поверхности земли (рис. 2.3) и рассчитать вначале проводимость растекания тока между реальным и мнимым электродом. Причем, ток, вытекающий из мнимого электрода должен быть равен по значению и по знаку току, выходящему из действительного электрода в землю. Емкость двух проводящих шаров (в предположении, что их электрические и геометрические оси совпадают) может быть определена по формуле (1.20), которую для данной системы электродов можно переписать в следующем виде:

(2.7)

Отметим, что если расстояние 2h между сферами мало по сравнению с радиусом R, то необходимо пользоваться более точным выражением для нахождения емкости, которое учитывает смещение электрических осей относительно геометрических

(2.8)

где

Таким образом, используя формулу (2.7) или (2.8), мы можем определить проводимость растекания тока между электродами

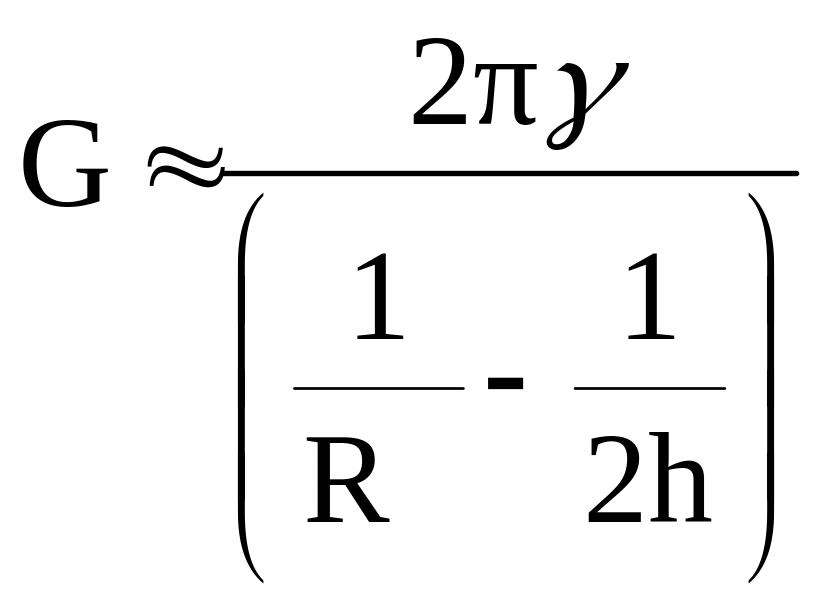
или

Проводимость заземления для действительного электрода, очевидно, равна половине проводимости, образованной электродом и его зеркальным изображением, то есть для нахождения проводимости заземлителя необходимо последние выражения разделить на два.