4. Переменное электромагнитное поле в диэлектрике

В предыдущих разделах были исследованы частные случаи электромагнитного поля, которые определялись или системой неподвижных и неизменных во времени зарядов (электростатическое поле), или неподвижных контуров с постоянными токами (стационарное электрическое поле и магнитное поле постоянных токов).

В общем случае изменяющихся во времени зарядов, токов, движущихся заряженных или намагниченных тел или движущихся контуров с токами в окружающем их пространстве существует переменное электромагнитное поле. Таким образом, под переменным электромагнитным полем понимают совокупность изменяющихся во времени и взаимно связанных и обуславливающих друг друга электрического и магнитного полей.

4.1. Плоская электромагнитная волна в диэлектрике. Скорость распространения электромагнитной волны

При исследовании процессов в переменном электромагнитном поле пользуются полной системой уравнений Максвелла.

Здесь - плотность тока переноса

,

где ₊ и _- - объемная плотность положительно заряженных частиц и отрицательно заряженных частиц, перемещающихся в пространстве со скоростью соответственно.

Для плоской, поляризованной электромагнитной волны, излучаемой источниками, не содержащими постоянных токов и зарядов (антенна), и распространяющейся в идеальном диэлектрике (=0), уравнения электромагнитного поля можно преобразовать к следующему виду:

(4.1)

(4.2)

Отметим, что электромагнитная волна называется плоской, когда векторы зависят только от одной координаты, например z.

Поляризованной называется такая волна, в которой вектор напряженности электрического поля все время остается параллельным некоторому направлению (например, как в нашем случае, оси ох), а вектор напряженности магнитного поля – другому (оси оy).

Такие условия обеспечиваются при излучении электромагнитных волн неподвижной антенной на достаточно большом расстоянии от нее.

Таким образом, в электромагнитной волне, свободно распространяющейся в однородном и изотропном диэлектрике, векторы взаимно перпендикулярны ( ).

Уравнения (4.1) и (4.2) можно преобразовать к следующему виду:

, (4.3)

где имеет размерность скорости.

Уравнение (4.3) является уравнением колебаний или волновым уравнением и относится к гиперболическому типу.

Как известно, решение такого уравнения всегда можно представить в виде:

. (4.4)

При этом составляющая Е_х1 называется прямо бегущей или прямой волной (перемещается в положительную сторону оси oz со скоростью ), а составляющая Е_х2 – обратно бегущей или обратной волной (перемещается в отрицательную сторону оси oz со скоростью ).

Используя выражения (4.1), (4.2) и (4.4) получаем формулу для напряженности магнитного поля

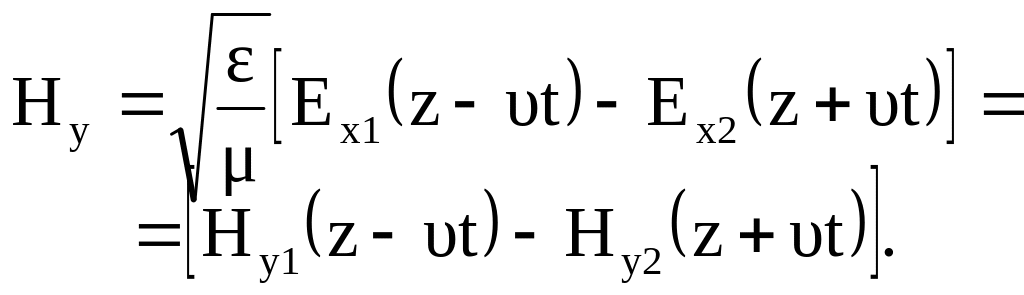
Составляющие Н_х1 и Н_х2 также называют прямой и обратной волной.

Таким образом, электромагнитная волна распространяется в пространстве со скоростью  (в прямом или в обратном направлении).

В частности, в пустоте (=₀, =₀) эта скорость равна скорости света (=2.998×10⁸м/с3×10⁸м/с).

Если существует только прямая или только обратная волна, то энергии электрического и магнитного полей равны между собой, так как при этом равны их объемные плотности

.

Отношение Е_х1/Н_у1==Z_в имеет размерность электрического сопротивления и называется волновым сопротивлением среды.

В частности, для пустоты Z_в=377Ом (Z_в =120).

Таким образом, для любой среды

.

В случае, если прямая электромагнитная волна распространяется в среде, абсолютное значение магнитной проницаемости которой =₁, а абсолютное значение диэлектрической проницаемости =₁, и подходит нормально (перпендикулярно) к плоской границе, разделяющей данную среду и среду с =₂ и =₂, то прямая волна (Е_х1=Е_1, Н_х1=Н_1) частично будет проходить сквозь поверхность раздела, образуя во второй среде преломленную (прямую) волну (Е_2, Н_2), а частично будет отражаться от поверхности раздела, образуя в первой среде отраженную (обратную) волну (Е_х2=Е_1, Н_х2=Н_1).

Соотношение между напряженностями поля для этих волн на поверхности раздела можно представить следующим образом:

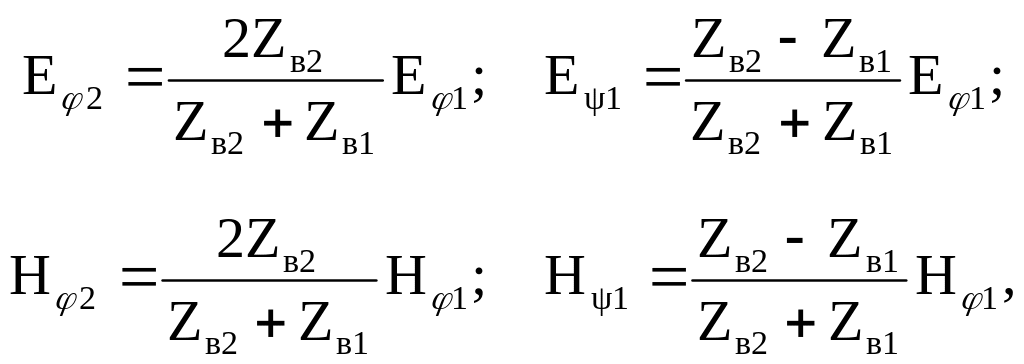
где -соответствующие волновые сопротивления первой и второй среды.

Если волновые сопротивления сред равны между собой (Z_в1= Z_в2), то отраженные волны отсутствуют.

В случае, когда источник (антенна) излучает электромагнитную волну, в которой напряженность электрического и магнитного поля изменяется по гармоническому закону, то для прямой волны

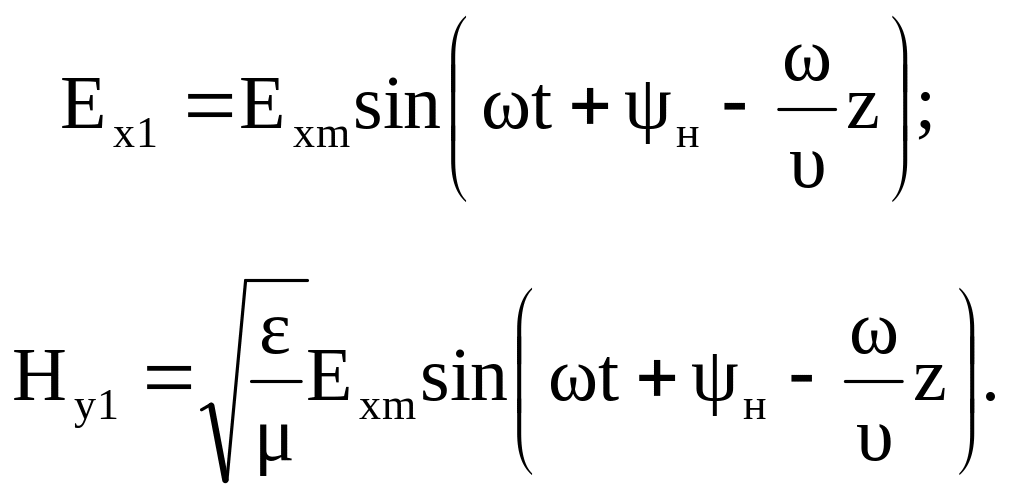
Здесь _н- начальная фаза;  - угловая частота колебаний (=2f).

Расстояние, на которое распространяется электромагнитная волна в течение одного периода колебаний Т (Т=1/f), называется длиной волны

 = Т = /f.

Из данного выражения видно, что длина волны в диэлектрике обратно пропорциональна частоте f. Так, при частоте f=1 МГц длина волны в пустоте равна 300 м, а при f=50Гц =6000 км.