3.6. Выражение магнитного потока через векторный потенциал

Установим связь между магнитным потоком Ф сквозь некоторую поверхность s и векторным потенциалом магнитного поля. Имеем (3.1)

Согласно теореме Стокса последнее выражение можно переписать в виде:

(3.10)

Таким образом, магнитный поток сквозь поверхность s равен линейному интегралу векторного потенциала по замкнутому контуру, ограничивающему эту поверхность.

3.7. Граничные условия

Н а поверхности раздела двух сред с различными магнитными проницаемостями (рис. 3.1) равны между собой касательные составляющие магнитного поля

(3.11)

и нормальные составляющие магнитной индукции

(3.12)

Здесь индекс 1 относится к первой среде, а индекс 2 – ко второй.

Условия (3.11) и (3.12) можно представить и в таком виде

и .

Из данных граничных условий можно получить еще одно условие - условие преломления линий поля при переходе их из одной среды в другую:

, (3.13)

где ₁ и ₂ - углы между вектором магнитной индукции (или напряженности) и нормалями к границе раздела сред.

При этом, если вектор напряженности перпендикулярен к границе раздела, то магнитная индукция не меняется при переходе из одной среды в другую, а напряженность поля меняется скачком.

Большое практическое значение имеет вопрос о характере магнитного поля в воздухе около поверхностей стальных частей различных электротехнических устройств. Магнитные проницаемости ферромагнитной среды и воздуха сильно разнятся между собой. Если магнитные силовые линии выходят из стали (например, с ₁ = 1000₀) в воздух (₂ = ₀), то, как следует из уравнения (3.13), угол ₂ будет много меньше угла ₁. Практически можно считать, что линии магнитной индукции в воздухе нормальны к поверхностям тел из ферромагнитных материалов.

3.8. Метод зеркальных изображений

Д ля расчета магнитных полей в неферромагнитных средах, ограниченных какой либо ферромагнитной поверхностью правильной формы или в которых есть геометрически правильной формы граница между двумя средами с различными магнитными проницаемостями, широко применяют метод зеркальных изображений.

Это искусственный прием расчета, в котором кроме заданных проводников с токами вводят еще дополнительные проводники, которые помещают там, где находятся зеркальные (в геометрическом смысле) отображения заданных проводников.

Рассмотрим поле прямолинейного провода с током I, расположенным на расстоянии h от плоской ферромагнитной поверхности (рис. 3.2).

Устраним мысленно ферромагнитную среду и заменим ее проводом, являющимся зеркальным изображением реального провода в поверхности раздела и имеющим ток такого же направления и такой же величины, как и ток реального провода (рис. 3.2). Действительный провод и его зеркальное изображение составляют двухпроводную линию. Поле от такой системы проводников с токами в области над проводящей средой останется таким же, как и в действительных условиях. В этом и заключается метод зеркальных изображений.

Э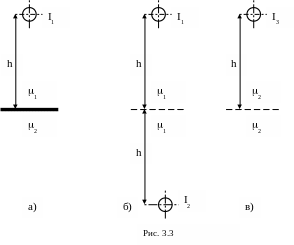 тот метод применим и при любом числе проводов, протянутых параллельно друг другу и параллельно плоской поверхности, ограничивающей ферромагнитную среду. Каждый провод должен быть зеркально отображен в поверхности ферромагнитной среды (направление тока остается неизменным), после чего ферромагнитная среда может быть мысленно удалена и рассмотрено поле совокупности действительных проводов и их зеркальных изображений.

Рассмотрим теперь поле прямолинейного провода с током I расположенного на расстоянии h от плоской границы раздела двух сред с разными магнитными проницаемостями (рис. 3.3, а).

Расчет поля в любой точке верхнего полупространства производят от двух проводников: заданного с током I₁ и дополнительного с током I₂. Причем не только верхнее, но нижнее полупространство заполнено (в расчетном смысле) средой с магнитной проницаемостью ₁, а дополнительный (фиктивный) проводник является зеркальным отображением действительного (в геометрическом смысле) проводника (рис. 3.3, б).

Поле в любой точке нижнего полупространства определяют как поле от дополнительного провода, по которому протекает ток I₃ и расположенного в той же точке, где находился действительный проводник. В этом случае, не только нижнее, но и верхнее полупространство заполняется средой с магнитной проницаемостью ₂ (рис. 3.3, в).

Токи I₂ и I₃ дополнительных проводников определяется с помощью следующих соотношений: