Решение игр вида 2хn и mх2

Графо-аналитический метод.

У таких игр всегда имеется решение, содержащее не более двух активных стратегий для каждого из игроков. Если найти эти активные стратегии, то игра 2 х n или m х 2 сводится к игре 2 х 2, которую мы уже умеем решать. Поэтому игры 2 х n и m х 2 решают обычно графоаналитическим методом. Рассмотрим решение матричной игры на примере.

Пример:

Решение:

					α
	1	4	7	1	2
	6	3	2	2
β	6	4	7		4

α= 2, β=4, α≠β, поэтому игра не имеет седловой точки, и решение должно быть в смешанных стратегиях.

1. Строим графическое изображение игры.

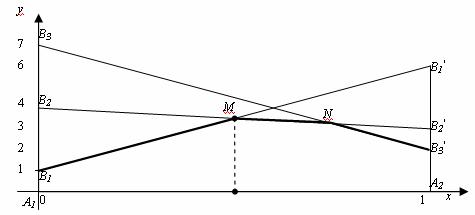
Если игрок B применяет стратегию В₁, то выигрыш игрока A при применении стратегии А₁ равен а₁₁ = 1, а при использовании А₂ выигрыш равен а₂₁ = 6, поэтому откладываем отрезки А₁В₁ = 1, А₂В₁^′ = 6 на перпендикулярах в А₁ и А₂ и соединяем их отрезком. Аналогично для стратегий В₂ и В₃ строим отрезки В₂ В₂^′ и В₃ В₃^′.

2. Выделяем нижнюю границу выигрыша В₁М N В₃^′ и находим наибольшую ординату этой нижней границы, ординату точки М, которая равна цене игрыγ.

3. Определяем пару стратегий, пересекающихся в точке оптимума М.

В этой точке пересекаются отрезки В₂В₂^′ и В₁В₁^′, соответствующие стратегиям В₁ и В₂ игрока B. Следовательно, стратегию В₃ ему применять невыгодно. Исключаем из матрицы третий столбец и решаем игру 2 x 2 аналитически:

  ; ; .

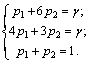
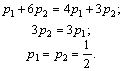
Ответ: γ = 7/2; P_A = (1/2; 1/2); Q_B = (1/6; 5/6; 0).

Аналогично решаются - игры.

Пример, ,

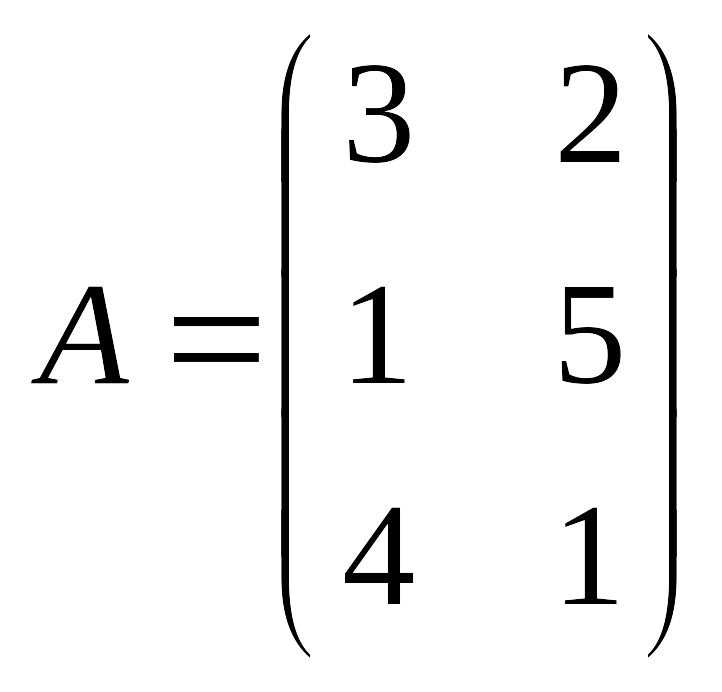Решение.

				α
	3	2	2	2
	1	5	1
	4	1	1
β	4	5	4

α= 2, β=4, α≠β, поэтому игра не имеет седловой точки, и решение должно быть в смешанных стратегиях.

1. Строим графическое изображение игры.

Если игрок А применяет стратегию А₁, то выигрыш игрока В при применении стратегии В₁ равен а₁₁ = 3, а при использовании В₂ выигрыш равен а₁₂ = 2, поэтому откладываем отрезки В₁А₁ = 3, В₂А₁^′ = 3 на перпендикулярах в В₁ и В₂ и соединяем их отрезком. Аналогично для стратегий А₂ и А₃ строим отрезки А₂ А₂^′ и А₃ А₃^′.

2. Выделяем нижнюю границу выигрыша А₃М А₂^′ и находим наибольшую ординату этой нижней границы, ординату точки М, которая равна цене игрыγ.

3. Определяем пару стратегий, пересекающихся в точке оптимума М.

В этой точке пересекаются отрезки В₂В₂^′ и В₁В₁^′, соответствующие стратегиям А₃ и А₂ игрока А. Следовательно, стратегию А₁ ему применять невыгодно. Исключаем из матрицы первую строку и решаем игру 2 x 2 аналитически:

  ; ; .

Ответ: γ = 7/2; P_A = (1/2; 1/2); Q_B = (1/6; 5/6; 0).