Раздел 2. Математическая статистика.

Глава 4. Статистические законы распределения случайных величин.

4.1. Основные задачи математической статистики (мс).

МС – это наука, которая разрабатывает математические методы, позволяющие на основе статистических данных делать выводы о вероятностных свойствах наблюдаемых явлений.

Основной круг задач, который изучается в МС.

1. Задача статистической оценки закона распределения.

2. Задача оценивания параметров распределения.

3. Проверка параметрических и непараметрических гипотез.

Для того, чтобы решить сформулированные выше задачи необходимо уметь:

1)Организовывать статистические наблюдения (собирать статистические данные);

2)Анализировать статистические данные;

3)Принимать решения, делать выводы и вырабатывать рекомендации на основе проведенной обработки статистических данных.

Все множество значений, которое может принять изучаемая случайная величина, в МС называют генеральной совокупностью.

Следует иметь в виду, что МС изучает только те данные, которые измерены в метрической шкале, то есть являются количественными (как уже отмечалось выше, в м.с. изучают значения с.в.!!. Как следует из определения с.в., это вещественная функция, заданная на всем множестве  со значениями в R). Математическая статистика не изучает качественные данные!! То есть, в этом разделе мы не будем изучать методы статистики (Статистика 2), при помощи которых можно изучать результаты опросов и т.п.

ОПРЕДЕЛЕНИЕ 4.1.1. Конечный набор значений, извлеченный из генеральной совокупности, при соблюдении следующих условий:

выбор производят случайным образом;

независимо друг от друга;

из одной и той же генеральной совокупности;

называют выборкой значений случайной величины или просто случайной выборкой и обозначают:

 х₁, х₂, …, х_n.

Количество элементов в выборке n называют объемом выборки.

Замечание. Важно помнить и понимать, что математическая статистика «работает» со случайной выборкой. Причем, не выборкой объектов, а с выборками значений некоторой с.в.!

Из определения выборки сформулируем основную гипотезу математической статистики, которая говорит о том, что:

1. Все выборочные значения хi являются случайными величинами.

2. Независимыми друг от друга.

3. Имеют один и тот же закон распределения.

Предполагается, что значения случайной величины (выборочные!! значения) равновероятны. Если их n, то считают, что каждое значение хi встречается в выборке с вероятностью 1/n.

Следует иметь в виду, что для того, чтобы наши выводы о генеральной совокупности, которые мы будем делать, изучив выборку из этой генеральной совокупности, были правомерными, объем выборки должен быть больше либо равен 30: n30. Если объем выборки меньше 30, то такую выборку называют выборкой малого объема. Именно такие выборки изучал Стьюдент.

Пример 4.1.1 Пример выборки значений с.в. - числа студентов ВШМ, находящихся в библиотеке за час до закрытия.

8, 7, 8, 5, 9, 10, 7, 5, 12, 13, 12, 5, 10, 8, 8, 11, 12, 11.

Выборку, все элементы которой расположены в порядке возрастания, называют вариационным рядом:

 х₁^*, х₂^*, … , х_n^*.

Пример 4.1.2. Для выборки из примера 4.1.1. вариационный ряд будет следующий:

Выборку значений с.в. (особенно больших объемов) обычно группируют в виде специальных таблиц. Такая работа облегчает дальнейшие расчеты, связанные со статистической обработкой и была особенна актуально, когда не было современной вычислительной техники. В наше время, большую часть этой работы нужно «перепоручать» ПК. Способы группировки информации зависят от того, с какой с.в. мы работаем: д.с.в или н.с.в.

При статистической обработке данных, в том случае, когда есть одинаковые значения и есть основание считать, что изучаемая случайная величина дискретная, для неё строят сгруппированный статистический ряд,

ОПРЕДЕЛЕНИЕ 4.1.2 Таблицу вида:

...

... ,

, .

Называют сгруппированным статистическим рядом. Здесь неповторяющиеся выборочные значения случайной величины x, расположенные в порядке возрастания, это число, показывающее, сколько раз значение встретилось в выборке (частота выборочного значения), объём выборки. Через обозначена относительная частота выборочного значения .

Пример 4.1.3. Постройте сгруппированный ряд для с.в. из примера 4.1.1.

Для непрерывной случайной величины строят интервальный статистический ряд. Для этого действуют по следующей схеме:

1. На первом шаге находят число интервалов r, на которые разбивается отрезок . Через и обозначены соответственно наименьшее и наибольшее выборочное значение. В частности, число r можно вычислить по следующей формуле:

,

то есть как целую часть числа 1+ 3,2lgn.

2. Затем вычисляют дину каждого интервала, на которые будут разбивать весь отрезок от наименьшего до наибольшего значения:

Причем, границы этих интервалов потом находят по формулам:

, ,

ОПРЕДЕЛЕНИЕ 4.1.3. Интервальным статистическим рядом называют таблицу вида:

...

... ,

, .

В приведенных формулах через обозначено число выборочных значений, попавших в интервал J_i (частота попадания выборочных значений в интервал с номером i, i=1,…,r), а через обозначена относительная частота.

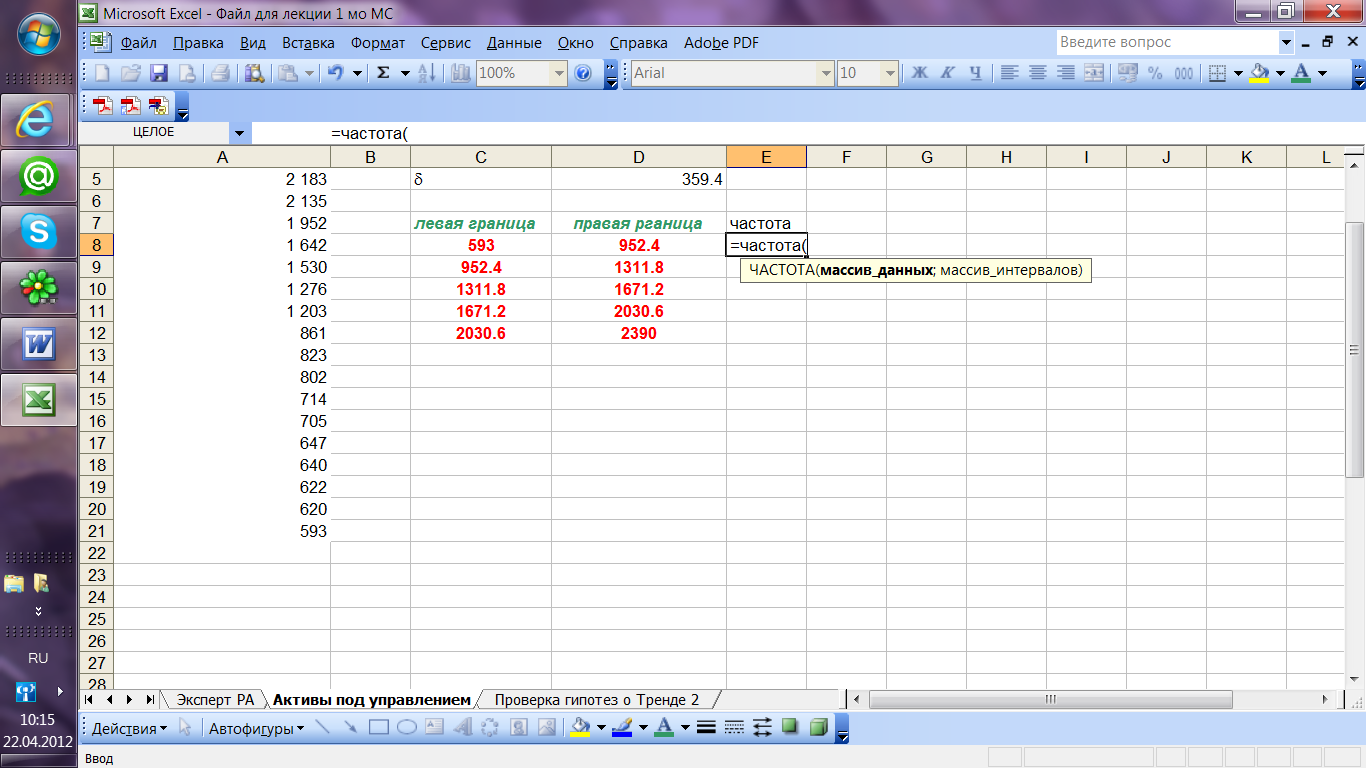
В интервальном ряде длина последнего интервала, вообще говоря, может не совпадать с длиной δ остальных интервалов.

Число интервалов r, на которые разбивается отрезок , может выбираться произвольно, а не по указанной формуле, главное чтобы оно было не меньше пяти и не больше двадцати пяти.