5. Рассмотрим ачх

График функции приведен на (рис.3)

Рис. 3

Необходимо убедиться в том, что функция достигает своего максимума в точке = . И этот максимум-

Докажем это.

Найдем производную .

Напомним:

В точке экстремума производная равна 0. Т.к. ,то можем записать в точке экстремума .

Производная :

=0

Если , то 4,5=4,5 и 4,5-4,5=0 , т.е производная в точке равна 0.

и

Известно, что для достаточно широкого класса внешних воздействий максимальная ошибка воспроизведения входного сигнала и максимальное отклонение в режиме стабилизации уменьшаются с ростом .

В установившемся режиме при :

Поэтому, чтобы иметь минимальное значение максимальной ошибки на установившемся режиме, надо выбирать как можно меньшее значение

(см. рис.3, где показана зависимость ), а, следовательно, большее значение

Однако с возрастанием степени устойчивости может возрасти величина . И тогда может быть нарушено условие |U(t)|≤ U_o, т.к. при гармоническом входном сигнале х (t)= x₀cos(ωt) установившийся режим для сигнала имеет вид

U_уcт(t)= x₀cos(ωt+ φ_U,x(ω))

x₀

Получим

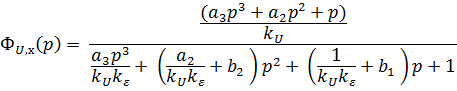
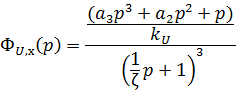
Далее в формулах ( нет времени переписывать формулы)

=

= = =

= (37)

Убедимся, что неравенство (36), вытекающее из ограничения на сигнал управления, эквивалентно неравенству:

(*)

Доказательство:

Как мы убедились выше

Обозначим , тогда

=

Возведем это выражение в квадрат, имея ввиду выполнение условия (36):

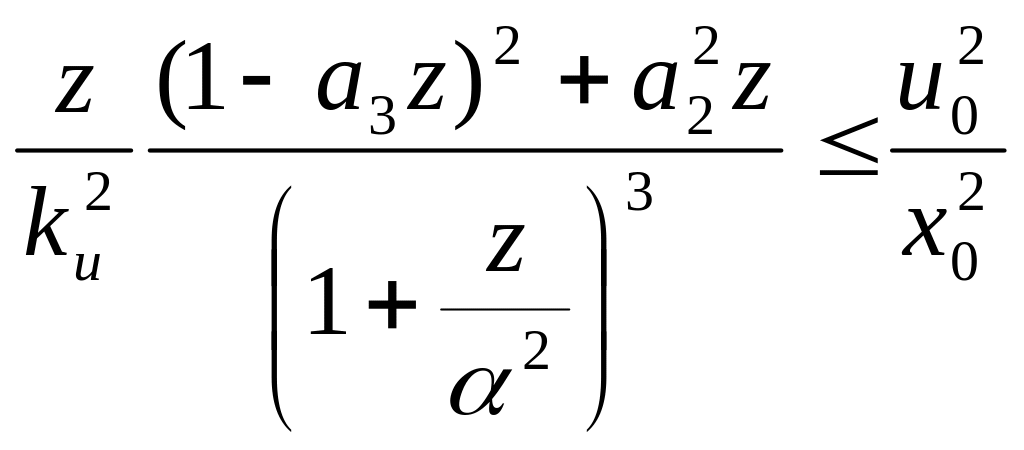
Разделим обе части неравенства на и преобразуем его:

Разделим на :

Обозначив левую часть неравенства , получили (*), что и требовалось доказать

Найдем =max при z₀= .

Для этого построим функцию

=0,6; ω₀ = 8,5; x₀= 0,7;

	0,1	0,5	5	20	30	40	50	60	72
	-7,9	-1,67	-0,08	0,2	0,211	0,22	0,225	0,23	0,25

На (рис.4) приведен график

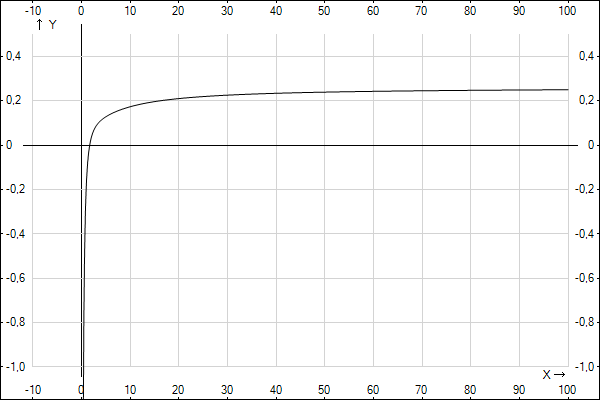
Рис.4

По (рис.4) видно, что функция возрастает на интервале z (0;z₀].

Следовательно, точка z₀ является искомой точкой максимума.

По формуле (39) найдем .

Именно эта и принимается за максимально допустимое значение степени устойчивости и по нему находятся числовые значения свободных параметров ,b₁,b_2.

Посчитаем ,b₁,b_2.

=1,6 = 12,8

Таким образом, мы получили:

Проверим систему на устойчивости по критерию Гурвица:

0,75*1,5> 0,125*1

1,125>0,125

Система устойчива.