104

Практичне заняття № 27. Афінні перетворення. Основні теоретичні факти.

Розглянемо відображення , яке кожну точку площини переводить у точку та задається співвідношеннями

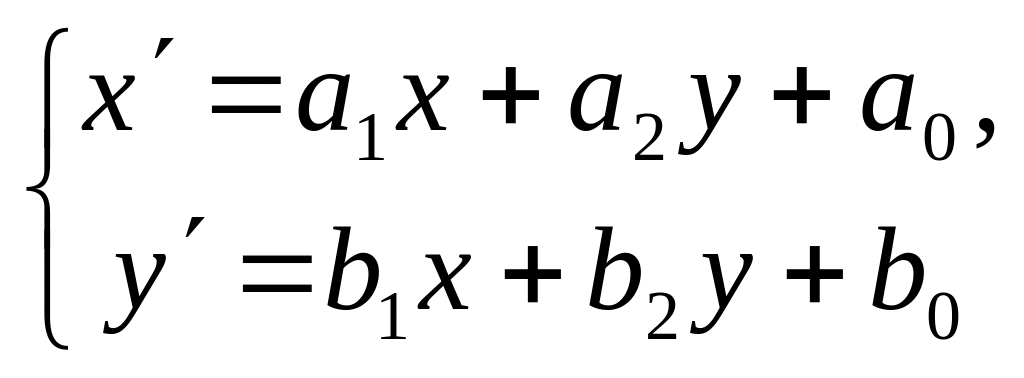. (1)

Матриця вважається невиродженою, тобто . Система рівнянь (1) однозначно розв’язується відносно та , зокрема

. (2)

Тому відображення , яке різні точки площини переводить у різні, буде перетворенням площини. Перетворення площини, яке задається рівностями (1), називається афінним.

Позначимо множину всіх афінних перетворень площини через та виберемо в ній два перетворення та , перше з яких задається рівностями (1), а друге – рівностями

, (3)

де - невироджена матриця.

Нехай при перетворенні точка перейде у точку , а при перетворенні точка перейде у точку . Перетворення, яке точку переводить у точку назвемо композицією перетворень та . Позначимо операцію композиції символом та знайдемо рівності, якими визначається відображення . Користуючись спочатку рівністю (3), а потім рівністю (1), дістаємо

, (4)

де . Очевидно, що матриця невироджена, оскільки . Тому рівність (4) визначає деяке перетворення . Із рівності (2) випливає, що разом із кожним перетворенням множина містить також обернене до нього перетворення . Таким чином пара є групою. Цю групу називають групою афінних перетворень. Роль нейтрального елемента в цій групі відіграє тотожне перетворення, яке задається рівностями . Група афінних перетворень є підгрупою групи перетворень площини.

Розглянемо інший спосіб, яким, крім рівностей (1), можна задавати афінні перетворення.

Поряд із деякою афінною системою координат , відносно якої розглядається точка та її образ при перетворенні (1) - точка , введемо у розгляд іншу систему координат із початком у точці та базисними векторами та , які є лінійно незалежними, оскільки . Образ точки при перетворенні (1) у новій системі координат має такі самі координати, як точка . Одержаний факт дозволяє задавати афінні перетворення наступним чином.

На площині вибираються дві довільні афінні системи координат (репери) і після цього точці, яка має відносно однієї із систем певні координати ставиться у відповідність точка із такими ж координатами, але уже відносно другого репера. Побудоване таким чином відображення є афінним перетворенням.

Перерахуємо основні властивості афінних перетворень.

1. Вектор при афінному перетворенні переходить у вектор з такими ж координатами.

2. При афінному перетворенні колінеарні вектори відображаються у колінеарні.

3. При афінному перетворенні пряма переходить у пряму, а паралельні прямі – у паралельні.

4. При афінному перетворенні відрізок переходить у відрізок, причому точка, яка ділить відрізок, який ми відображаємо, у деякому відношенні, переходить у точку, яка ділить образ відрізка у тому ж відношенні.

5. При афінному перетворенні півплощина перетворюється у півплощину.

6. Існує єдине афінне перетворення, яке одну трійку неколінеарних точок (тобто точок, які не лежать на одній прямій) переводить в іншу трійку неколінеарних точок.

Для того, щоб задати перетворення, яке три неколінеарні точки переводить у три неколінеарні, достатньо побудувати дві афінні системи координат та , де , , , . Афінне перетворення, яке визначається цими двома системами координат, переводить точки та відповідно у точки та , і є шуканим.

Назвемо фігуру афінно еквівалентною фігурі , якщо в групі афінних перетворень знайдеться перетворення, яке фігуру переводить у фігуру .

Відношення афінної еквівалентності має властивості рефлективності, симетричності та транзитивності. Це означає, що:

1) кожна фігура афінно еквівалентна сама собі (вона переводиться в себе тотожнім перетворенням);

2) якщо фігура афінно еквівалентна фігурі то фігура афінно еквівалентна фігурі , оскільки вона переводиться в неї оберненим перетворенням;

3) якщо фігура афінно еквівалентна фігурі , а фігура - фігурі , то фігура афінно еквівалентна фігурі , оскільки вона переводиться в неї перетворенням, яке є композицією двох перетворень, перше з яких переводить у , а друге - у .

Наведемо приклади афінно еквівалентних фігур.

1 ). Два довільні трикутники афінно еквівалентні.

2). Два опуклих чотирикутники будуть афінно еквівалентними, якщо точка перетину ділить їхні діагоналі в одному і тому ж відношенні.

На рисунку 1 зображено чотирикутники та . Вони будуть афінно еквівалентними, якщо виконуються рівності та .

3). Два довільні еліпси, дві гіперболи та дві довільні параболи афінно еквівалентні.

Існує 9 класів афінно еквівалентних ліній другого порядку: еліпси (дійсні та уявні), гіперболи, параболи, дійсні прямі, які перетинаються, паралельні або співпадають та уявні прямі, які перетинаються у дійсній точці або паралельні.

Дамо відповідь на питання, як при афінних перетвореннях змінюються площі відповідних фігур. Розпочнемо із трикутника. Нехай у прямокутній декартовій системі координат три неколінеарні точки визначають деякий трикутник з площею . При афінному перетворенні

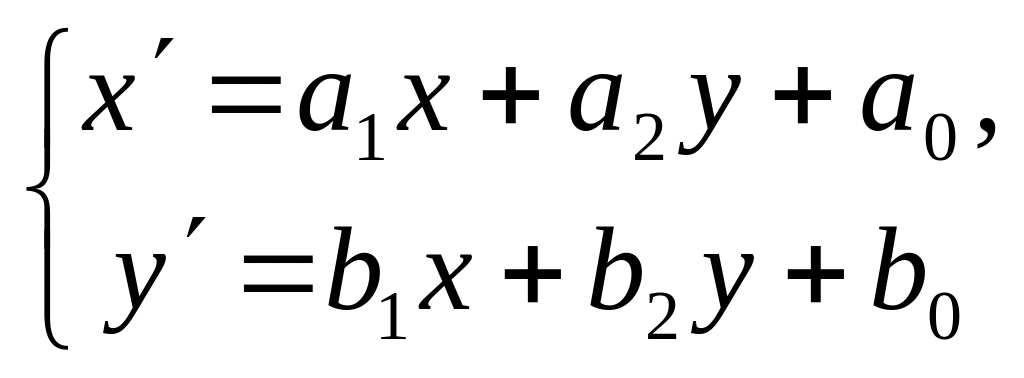
вершини трикутника перейдуть у нові точки . Площу трикутника можна обчислити за допомогою співвідношення

=

При афінному перетворенні зберігається відношення площ двох довільних трикутників.

Оскільки площі більш складних геометричних фігур можна обчислювати за допомогою граничного переходу через площі вписаних у ці фігури трикутників, то можна стверджувати, що при афінному перетворенні зберігається відношення площ двох довільних фігур.