Лабораторные работы №2,№3

Исследование линейных неразветвленных и разветвленных

цепей синусоидального тока

Цель работы: 1. Изучение основных законов цепи переменного тока;

2. Освоение методики расчета и построение векторных диаграмм при последовательном и параллельном соединениях элементов.

1. Основные теоретические положения

1. Общие понятия и определения

Переменными называются ЭДС, напряжения и токи, которые периодически изменяются во времени (рис. 1, а, б, в). В электроэнергетике наибольшее применение получили переменные токи, напряжения и ЭДС, величина и направление которых периодически изменяются по закону синуса (рис. 1, б). Эти токи, напряжения и ЭДС называются синусоидальными. В некоторых устройствах используется токи, напряжения и ЭДС, которые периодически изменяют только свою величину (рис. 1, в). Такие токи, напряжения и ЭДС называются пульсирующими.

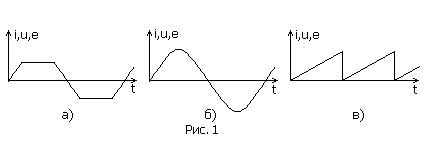Значения переменных величин: ЭДС, напряжений, токов и мощностей в произвольный момент времени t - называются мгновенными и соответственно обозначаются буквами .

Основные соотношения между электрическими величинами, установленные для цепей постоянного тока, остаются справедливыми и для мгновенных значений этих величин в цепях переменного тока:

, , , .

Выражения мгновенных значений синусоидальных токов, напряжений, ЭДС определяются тригонометрическими функциями

, , , единственной переменной в правой части которых является время . График мгновенных значений тока , напряжения , ЭДС показан на рис.2.

Наибольшее из мгновенных значений тока, напряжения, ЭДС называется максимальным (амплитудным) значением и обозначается .

А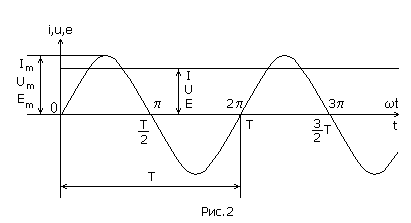 ргумент синуса , измеряемый в радианах, определяет фазный угол синусоидальной функции в любой момент времени и называется фазой. Величина определяет число радианов, на которое изменяется фаза колебаний за секунду, и называется угловой частотой.

Промежуток времени, в течение которого завершается один полный цикл изменения синусоидальной величины, называется периодом обозначается через Т и измеряется в секундах. Величину, обратную периоду, называют частотой и обозначают . Частота определяется количеством периодов в секунду: и измеряется в герцах (Гц). Частота промышленного тока в России равна 50 Гц.

Синусоидальные ЭДС, ток и напряжение являются периодическими функциями времени. Через промежуток времени фаза колебаний изменяется на угол следовательно, период и угловая частота связаны соотношением . Отсюда

.

Для оценки эффективности синусоидального тока используется действующее значение тока, равное такому постоянному току, который имеет такой же тепловой эффект, как и синусоидальный. Таким образом действующее значение тока равно среднеквадратичному значению за период.

= = .

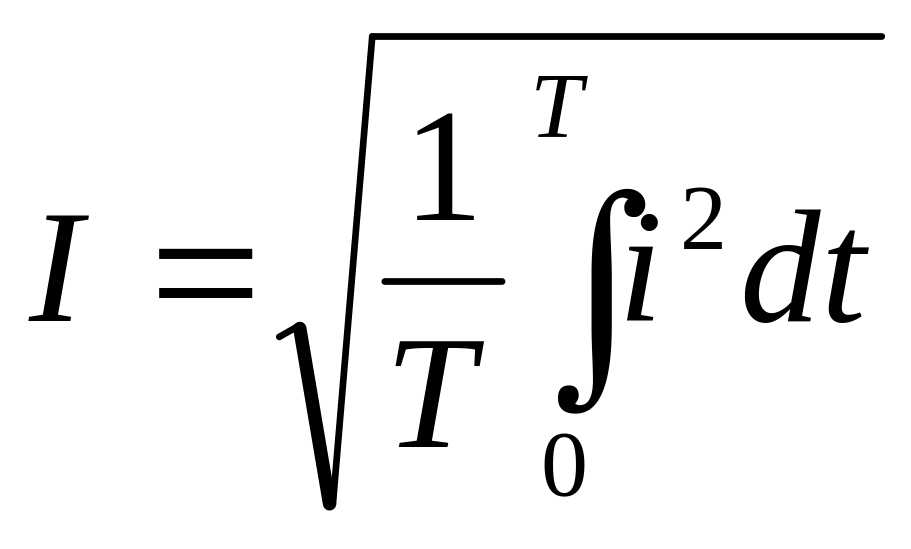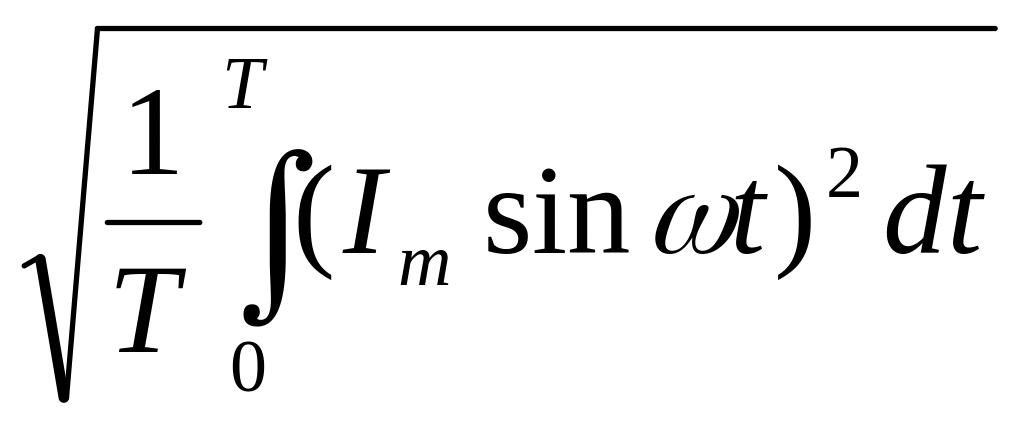Аналогично определяют действующие значения ЭДС и напряжений:

, ,

где - действующие значения тока, ЭДС, напряжения.

Приборы для измерения переменных токов и напряжений градуируют в действующих значениях.

В общем случае аналитическое выражение для синусоидальных тока, напряжения, ЭДС можно представить уравнениями

, , .

Величину , определяющую значение синусоидальной величины в начальный момент времени ( ), называют начальной фазой. На графике (рис. 3, а) начальные фазы и определяют значения ЭДС и в начальный момент времени.

При совместном рассмотрении нескольких синусоидальных электрических величин одной частоты обычно интересуются разностью их фазовых углов, называемой углом сдвига фаз. Угол сдвига фаз между током и напряжением участка цепи принято обозначать буквой и определять вычитанием начальной фазы тока из начальной фазы напряжения (рис.3,б):

.

Угол - величина алгебраическая. Если то , при этом говорят, что напряжение опережает ток по фазе или ток отстает по фазе от напряжения. В случае , т. е. напряжение отстает по фазе от тока или ток опережает напряжение.

С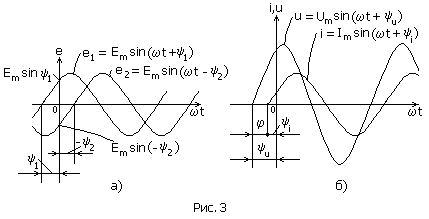 овокупность нескольких векторов, изображающих синусоидально изменяющиеся величины одной и той же частоты, называется векторной диаграммой.

На рис. 4, а изображены графики изменения во времени двух синусоидальных величин и а также векторная диаграмма этих величин (рис. 4, б).

На векторной диаграмме синусоидальные величины и изображены в виде векторов, вращающихся с угловой скоростью против направления движения часовой стрелки. Длины векторов ( в масштабе построения) берутся равными амплитудным значениям и синусоидальных величин и , а расположены вектора под углами и к горизонтальной оси.

Векторные диаграммы позволяют производить сложение и вычитание синусоидальных величин по правилам сложения и вычитания векторов.

Н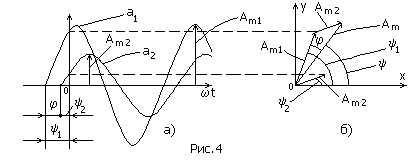 а рис. 4, б показано сложение синусоидальных величин и , в результате чего определяется амплитудное значение и начальная фаза синусоидальной величины .

Векторные диаграммы используются главным образом для определения действующих значений синусоидальных величин и сдвигов фаз между ними, поэтому более удобно длины векторов на диаграммах принимать равными действующим значениям синусоидальных величин.

Вращающиеся векторы синусоидальных ЭДС, напряжений и токов можно изобразить на комплексной плоскости, при этом ось абсцисс плоскости декартовых координат совмещают с осью действительных или вещественных величин комплексной плоскости. Любой вектор, изображенный на комплексной плоскости (рис. 5) можно аналитически выразить комплексным числом

где и - проекции вектора на действительную и мнимую оси прямоугольной системы координат, .

П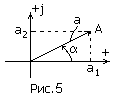 ри расчетах используются две формы записи комплексного числа:

алгебраическую:

,

показательную:

.

Переход от алгебраической формы к показательной осуществляется по следующим формулам:

модуль комплексного числа;

аргумент комплексного числа;

если то .

При переходе от показательной формы к алгебраической используются следующие формулы:

.

Изображение синусоидальных тока , напряжения и ЭДС в комплексной форме:

, где комплексные действующие значения тока, напряжения, ЭДС, действующие значения тока, напряжения, ЭДС.

Сопротивление участка цепи (рис. 6) в комплексной форме записывается следующим образом :

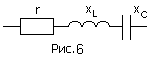, где

комплексное полное сопротивление участка цепи; полное сопротивление участка цепи; - угол сдвига фаз между током и напряжением участка цепи (рис. 6).