2. Построение сети общего вида

Построение сети общего вида (или сети типа PERT) отличается от построения сети типа «дерево», которая имеет более простую структу­ру и используется для описания процесса производства изделия.

Понятие правильной нумерации событий сети

Задача по построению сети общего вида (типа PERT) состоит в том, чтобы, имея список работ с указанием непосредственно им пред­шествующих, построить ориентированный граф, работы (дуги) кото­рого определяются номерами начального и конечного событий, с обя­зательным соблюдением условия, что для любой работы сети /' <у, где i и j — номера начального и конечного событий этой работы^I соответ­ственно.

Примечание. Для нумерации событий сети используются числа нату­рального ряда без пропусков.

На рисунке 2.3 показан фрагмент сетевого графа с неправильной нумерацией событий работы (5—4), где номер начального события больше номера конечного события.

Рис. 2.3. Фрагмент сетевого графа с неправильной нумерацией событий работы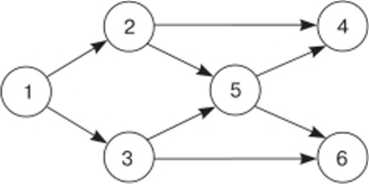

Определение ранга работы

Процесс нумерации событий сети общего вида происходит в два этапа. На первом проводятся расчеты по алгоритму топологической схемы. Результат расчетов но нему — предварительная нумерация со­бытий, отражающая только последовательность и взаимосвязь работ. Окончательной нумерацией результаты расчетов по этому алгоритму служить не могут, потому что события оказываются занумерованными числами натурального ряда с пропусками, для ряда работ сети может нарушиться требование / </, т.е. номер начального события работы мо­жет оказаться больше, чем номер ее конечного события.

На втором этапе переход к окончательной нумерации событий обеспечивают расчеты по алгоритму правильной нумерации. Клю­чевое понятие при правильной нумерации событий понятие ранга работы. Под ним понимается максимальное количество работ от на­чального события сети до конечного события данной работы.

Следствие. У всех работ с общим конечным событием значения рангов одинаковы (рис. 2.4 и табл. 2.4 иллюстрируют определение ран­гов работ сетевой модели).

Рис. 2.4. Определение рангов работ сетевой модели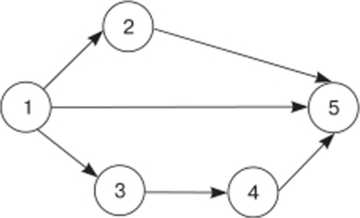

Шифр	Ранг
1-2	1
1-3	1
3-4	2
1-5	3
2-5	3
4-5	3

Ранг — это характеристика работы, необходимая для установле­ния последовательности нумерации событий сети: события нумеру­ются в порядке возрастания ранга работы. Следовательно, в резуль­тате правильной нумерации работы с меньшим шифром всегда будут предшествовать работам с большим шифром, возникновение обратной ситуации (когда работы с большим шифром предшествуют работам с меньшим шифром) невозможно.

Внимание! Прежде, чем приступать к расчетам по алгоритму «тополо­гическая схема», необходимо убедиться, что исходная информация для построения сетевой модели задана корректно.