2. Оптимизация сети по времени

Для оптимизации работ проекта по времени для сетевых моделей можно применять методы перебора вариантов комбинаций длительно­стей либо эвристические методы. Интересные результаты получаются при проведении оптимизации работ проекта одновременно по време­ни и стоимости. Знание зависимости стоимости работы от ее длитель­ности позволяет определить множество работ, которые необходимо ускорить за счет дополнительных затрат, чтобы выполнить проект в заданное время с минимальной стоимостью. Зависимость стоимости выполнения работ проекта от времени их выполнения представляется в виде убывающей функции (рис. 3.2)', следовательно, коэффициент стоимости (K_CQ_jy) определяется следующим образом:

/*>яапр /*>норм _ i-j Ф -» л норм _ . напр ’

Ч -) Ч-j

где C/L^aj^lp и С/1_°_/^рм — стоимости выполнения работы в напряженном и нор­мальном режимах соответственно:

¹ Кофман А., Дебазей Г. Сетевые методы планирования и их применение / пер. с франц. М.: Прогресс, 1968.

78

и гД°Р^м — время выполнения работы в нормальном и напряженном реж 11 мах соответстве! шо.

Рис. 3.2. Зависимость стоимости выполнения работы от времени ее выполнения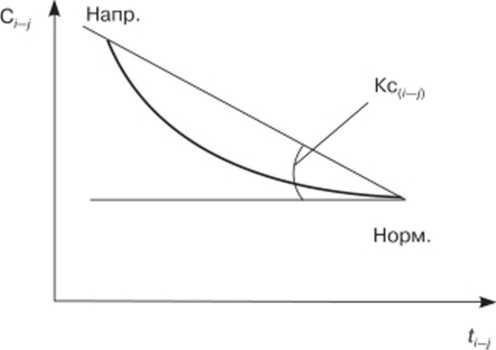

Стоимость работы, длительность которой лежит в пределах меж­ду нормальной и напряженной оценками, с учетом этого коэффициен­та рассчитывается по следующей формуле:

гч у-»ноpn.iv- /.норм -паирч

Ч-Х'-,) Ч-у >-j >'

Следовательно, задачу оптимизации проекта по времени и стои­мости можно свести к уменьшению времени выполнения «дешевых» работ критического пути. В ряде случаев возникает необходимость оптимизации сети только по времени.

Необходимость и цель оптимизации сетевого графика по времени

После построения и расчета сетевого графика производится со­поставление его расчетного цикла, т.е. критического пути, с отрезком времени между директивным сроком выполнения комплекса работ но проекту и наиболее реальным ранним сроком начала выполнения этих работ. Если критический путь не превышает заданного срока (рис. 3.3, а и в), то график утверждается и служит документом для оператив­ного планирования и регулирования хода работ. В том случае, когда в соответствии с расчетными параметрами графика выполнить весь комплекс работ к директивному сроку не представляется возможным (рис. 3.36), необходима корректировка (оптимизация) исходного гра­фика но времени.

^;t

Г^КР

Начало работ ^G Окончание работ

по проекту по проекту

Директивный срок

АГ.

Л

//

V

V

Начало работ по проекту

-КР

Окончание работ по проекту

б

ДМР

Директивный срок

Г

-I

7~у+ ►

I'—

Начало работ по проекту

V

■ КР

А ■

Окончание работ по проекту

в

Рис. 3.3. Критический путь и установленный директивный срок: а — директивный срок больше времени работы над проектом; б — директивный срок меньше времени работы над проектом; в — директивный срок равен времени работы над проектом

Цель корректировки — приведение расчетных (временных) па­раметров исходного сетевого графика (см. рис. 3.36) в соответствие с установленным директивным сроком (см. рис. З.Зв). Эта корректи­ровка может осуществляться за счет сокращения продолжительности исполнения работ, которое может быть достигнуто путем:

• привлечения дополнительных мощностей из других подраз­делен ий предприятия;

• организации сверхурочных работ:

• изменения технологии обработки узлов и деталей;

• организации параллельных (совмещенных) работ;

• пересмотра технологической последовательности работ;

• различных организационных мероприятий и т.д.

Условие, необходимое для осуществления

оптимизации сети по времени

Такая корректировка становится возможной, если для каждой из работ графика существует не только нормальная, но и уменьшенная до допустимого уровня длительность выполнения работы, г.е. напряжен­ная, ее величина. Такие величины могут быть рассчитаны на основе обработки экспертных оценок (например, с помощью метода индекс­ной группировки мнений экспертов, подробно рассмотренного в раз­деле III). Рассмотрим, каким образом может решаться задача сокраще­ния длительности выполнения всего комплекса работ сети.

Допустим, дана сетевая модель со следующими длительностями работ в нормальном и напряженном режимах исполнения (табл. 3.4). Требуется выполнить весь комплекс работ этой сети за 16 временных единиц.

Таблица 3.4

Оценки длительностей выполнения работ сети

Начальное событие, / Конечное событие, j	f норм	^ напр
1 2	3	2
1 3	2	2
1 4	2	1
2 6	4	2
3 6	10	6
4 5	1	1
5 6	10	6
5 7	3	3
6 7	5	4
7 8	2	2

Для решения задачи рассчитаем параметры работ данной сети в нормальном режиме исполнения, используя описанный выше алго­ритм «параметры» (табл. 3.5).

Таблица 3.5

Временные параметры работ сети в нормальном режиме исполнения

/	i	и	,?н 1ч	#р° *</	♦ пн *»/	*по li		га
1	2	3	0	3	6	9	6	0
1	3	2	0	2	1	3	1	0
1	4	2	0	2	0	2	0	0
2	6	4	3	7	9	13	6	6
3	6	10	2	12	3	13	1	1
4	5	1	2	3	2	3	0	0
5	6	10	3	13	3	13	0	0
5	7	3	3	6	15	18	12	12
6	7	5	13	18	13	18	0	0
7	8	2	18	20	18	20	0	0

Анализируя табл. 3.5, делаем вывод: критический путь этой сети составляет 20 временных единиц, что больше требуемого срока. Кри­тический путь представлен следующей цепочкой работ (шифр каждой работы составлен из номеров начального и конечного событий): 1—4,

4. 5, 5—6. 6—7, 7—8. В таблице 3.5 и далее работы критического пути и их временные параметры выделены жирным шрифтом.

Проверим, насколько реально выполнить комплекс работ сети за 16 временных единиц, т.е. сократить длительность критического пути на четыре единицы времени. Для этого рассчитаем параметры работ данной сети в напряженном режиме исполнения, используя алгоритм «параметры» (табл. 3.6).

Таблица 3.6

Временные параметры работ сети в напряженном режиме исполнения

/	/	и	fPH Ч	/Р°	.пн Ч	*по Ч		Ч
1	2	2	0	2	4	6	4	0
1	3	2	0	2	0	2	0	0
1	4	1	0	1	0	1	0	0
2	6	2	2	4	6	8	4	4
3	6	6	2	8	2	8	0	0
4	5	1	1	2	1	2	0	0

Окончание

/	/'	ч	1ч	tt°	* пн *■/	♦ по Ч	I гч
5	6	6	2	8	2	8	0	0
5	7	3	2	5	9	12	7	7
6	7	4	8	12	8	12	0	0
7	8	2	12	14	12	14	0	0

Анализируя табл. 3.6, делаем вывод: критический путь этой сети составляет 14 временных единиц, что меньше требуемого срока. Сле­довательно, срок в 16 единиц времени для выполнения всего комплек­са работ сети реален. Критический путь в условиях напряженного ре­жима представлен двумя цепочками работ. Первая цепочка: 1—3, 3—6, 6—7, 7—8, вторая — 1—4, 4—5, 5—6, 6—7, 7—8. Чтобы выполнить ком­плекс работ сети за 16 единиц времени, необходимо изменить длитель­ности выполнения ряда работ в пределах их нормальной и напряжен­ной оценок. Значит, возникает вопрос о выборе таких работ.

Поскольку срок выполнения всего комплекса работ сети опреде­ляется величиной критического пути, то возникает желание сокра­тить длительности работ именно критического пути. Здесь возможны следующие решения. Во-первых, изменение длительностей всех работ критического пути таким образом, чтобы их суммарное сокращение составило четыре единицы времени, во-вторых, сокращение длитель­ности какой-либо продолжительной работы на то же время. Проведем расчеты по первому из предложенных вариантов. Установим, напри­мер, следующие длительности выполнения работ критического пути (табл. 3.7).

Таблица 3.7