Глава 3

РАСЧЕТ ВРЕМЕННЫХ ПАРАМЕТРОВ СЕТИ БЕЗ УЧЕТА РЕСУРСНЫХ ОГРАНИЧЕНИЙ

Сетевая модель полностью отражает технологию процесса выпол­нения всего комплекса работ. На базе сетевой модели можно получить так называемый сетевой график, рассчитав по алгоритму «временные параметры сети» временные характеристики каждой работы сети: ран­нее и позднее начало, раннее и позднее окончание, полный и частный резервы времени.

1. ОПРЕДЕЛЕНИЕ ВРЕМЕННЫХ ПАРАМЕТРОВ СЕТИ

1. Алгоритм «временные параметры сети»

Исходная информация: сетевая модель, а также длительности выполнения работ сети (табл. 3.1).

Таблица 3.1

Исходные данные для реализации алгоритма «временные параметры сети»

№ п/п	Шифр работы (номера событий)		Длительность выполнения работы, Ц
	начальное,У	конечное,/
1	2	3	4

Условные обозначения:

1. j — начальное и конечное событие рассматриваемой работы:

8. i — начальное и конечное событие предшествующей работы: j, к — начальное и конечное событие предшествующей работы: tjj — длительность выполнения рассматриваемой работы; t-J^u — ранний срок начала рассматриваемой работы;

(Г — ранний срок начала последующей работы;

/,5^>() — ранний срок окончания рассматриваемой работы; t/J° — ранний срок окончания предшествующей работы;

• поздний срок начала рассматриваемой работы; tjil¹¹ — поздний срок начала последующей работы; tjj° — поздний срок окончания рассматриваемой работы;

r,j — частный резерв времени рассматриваемой работы;

Ry — полный резерв времени рассматриваемой работы; tc^v — продолжительность критического пути.

Расчеты по алгоритму «временные параметры сети» (в дальней­шем по тексту — «параметры») удобно производить в таблице, структу­ра которой соответствует представленной в табл. 3.2. Исходная инфор­мация для практической реализации данного алгоритма помешается в графах 1—4.

Таблица 3.2

Расчет параметров сети

№ п/п	Шифр работы (номера событий)		и	*РН ‘V	#.РО 1ч	*пн	*по	**	'#
	начальное, /	конечное,/'
1	2	3	4	5	6	7	8	9	10

Шаг 1^[. Присвоение всем начальным² работам сетевого графа сроков ранних начал и окончаний:

.рн _ ₀. _tро _ * рн ₊ .

4j *■ij ^Iij ^vtj'

Шаг 2. Расчет для всех остальных работ сроков ранних начал и окончаний:

“ max t*° = t?^H + Ц.

ШагЗ. Определение длительности критического пути:

t£^p - max <^⁰}.

Шаг 4. Присвоение всем конечным работам сетевой модели сро­ков поздних начал и окончаний:

ЛЮ ₌ /КР. ,.пн _ * по _ *

tjj L(] , Ljj Ljj Ljj.

Шаг 5⁴. Расчет для всех остальных работ сроков поздних начал и окончаний:

cj¹⁰ - min $f"}; t?" = tf° - t_tj.

Шаг в. Определение частного резерва. Определение для всех ра­бот полного и частного резервов:

/? . - * по _ * ро _ _t пи _ _t ph. _ * рн _ ,РО

l\jj Ljj ljj Ljj ljj , I jj Ijfr ljj

Примечание. Для конечных работ сетевой модели частный резерв опре­деляется так:

_ . кр , РО ^ri)~^lG ~Ч) •

Полный резерв работы — это время максимально возможной от­срочки начала работы или время максимально возможного увеличе­ния длительности выполнения работы (при отсчете от раннего начала работы) без нарушения общего срока выполнения всего комплекса ра­бот сети, соответствующего длине критического пути (или позднему сроку свершения конечного события сети).

Частный резерв работы — это максимальное время, на которое возможно отсрочить начало работы или увеличить длительность ее выполнения (при отсчете от раннего начала работы), чтобы не нару­шить сроки ранних начал последующих работ сети.

Установленные параметры сетевой модели позволяют организо­вывать гармоничное ведение производственных процессов, компенси­руя возникающие отклонения путем обоснованного перераспределения ресурсов, сосредоточивая внимание на работах критического пути.

Критический путь — максимальная по длительности, непрерыв­ная цепочка работ от начального события сети до конечного — характе­ризуется работами, у которых ранние и поздние сроки их начала (или их окончания) совпадают. Кроме того, у работ, лежащих на критиче­ском пути, полный и частный резервы равны нулю¹.

2. Пример расчетов по алгоритму «временные параметры сети»

Исходная информация для примера — графы I—4 табл. 3.3.

Таблица 3.3

Исходная информация для примера расчетов по алгоритму «временные параметры сети»

№	Шифр работы (номера событий)		*«/	f.pn	гр° Ч	*пн Ч	*по Ч	Ъ	Г.
п/п	начальное, /'	конечное./'							Гч
1	2	3	4	5	6	7	8	9	10
1	1	2	3	0	3	2	5	2	0

¹ Если полный резерв работы равен нулю, значит, работа лежит на критическом пути и, следовательно, частный резерв этой работы также равен нулю. Обратное утверж­дение верно не всегда, т.е. из равенства нулю частного резерва не всегда следует, что работа лежит на критическом пути и ее полный резерв равен нулю.

1	2	3	4	5	6	7	8	9	10
2	1	3	2	0	2	6	8	6	0
3	1	4	5	0	5	0	5	0	0
4	2	4	0	3	3	5	5	2	2
5	2	6	3	3	6	8	11	5	5
6	3	5	4	2	6	8	12	6	0
7	3	7	4	2	6	10	14	8	8
8	4	6	6	5	11	5	11	0	0
9	5	7	2	6	8	12	14	6	6
10	6	7	3	11	14	11	14	0	0

Шаг 1. Присвоение веем начальным работам сетевого графа сро­ков ранних начал и окончаний.

Номер начального события таких работ равен единице, следова­тельно, это работы (1—2), (1—3) и (1—4):

tl'"₂ - 0, tfS-[ - f,^pJ^ + С,_₂ -0 + 3-3;

(Г_л = 0. tfS.\ = г,^р_^н₃ +1,_ з = 0 + 2 = 2;

г,^р_^н₄ = 0. f,^P04 = (,^р_^н₄ + f,_₄ = 0 + 5 = 5.

Шаг 2. Расчет для всех остальных работ сроков ранних начал и окончаний.

У работ (3—5) и (3—7) также одна предшествующая работа — ра­бота (1—3), значит, срок раннего начала работ (3—5) и (3—7) — это срок раннего окончания работы (1—3), следовательно:

У работ (2—4) и (2—6) всего одна предшествующая работа — ра­бота (1—2), значит, срок раннего начала работ (2—4) и (2—6) — это срок раннего окончания работы (1—2), следовательно: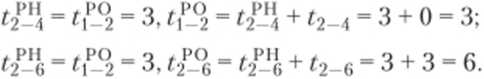

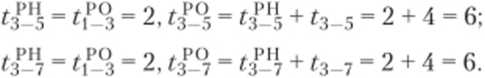
Работе (4—6) предшествуют две работы — работы (1—4) и (2—4), значит, срок раннего начала работы (4—6) определяется как максимум из ранних окончаний работ (1—4) и (2—4), следовательно:

гй ^{= тах 1}2-а) = max (5,3} = 5 = = //Jf, + f₄_₆ = 5 + 6=11.

У работы (5—7) всего одна предшествующая работа — рабо­та (3—5), значит, срок раннего начала работы (5—7) — это срок раннего окончания работы (3—5), следовательно:

*5-^7 ⁼ ^3—5 ⁼ 6* *5—7 ^{= +} *5-7 = 6 + 2 = 8.

Работе (6—7) предшествуют две работы — работы (2—6) и (4—6), значит, срок раннего начала работы (6—7) определяется как максимум из ранних окончаний работ (2—6) и (4—6), следовательно:

*6-7 - шах to-®, " ^max {6, И} - 11, t™ - +1₆-7 - И + 3 - 14.

Шаг 3. Определение длительности критического пути, соответ­ствующей максимальному значению по графе 6 табл. 3.3:

tc^P - max {£,у°} ■ шах {3, 2, 5, 6, И, 8,14} - 14.

Шаг 4. Присвоение всем конечным работам сетевой модели сро­ков поздних начал и окончаний. Помер конечного события таких работ соответствует максимальному значению по графе 3 табл. 3.3, т.е.у = 7, следовательно, это работы (6—7), (5—7) и (3—7).

*б^П-°7 = *<Р = 14, = е°7 - *6—7 =14-3=11:

,по _ _tKi> _{ш м} ,п_н - ,П0 _ _{t5 7} - 14 _ 2 - 12;

*з^П-°7 = *<Р = 14, г₃^п-^н7 = *з-°7 - *3—7 = 14 - 4 = 10.

Шаг 5. Расчет для всех остальных работ сроков поздних начал и окончаний. Работы (4—6) и (2—6), имеющие общее конечное собы­тие, предшествуют всего одной работе — работе (6—7), значит, срок позднего окончания работ (4—6) и (2—6) — это срок позднего начала работы (6—7), следовательно:

*4^ПОб - -11, - tJL°_e -1₄-₆ - И - 6 - 5;

*2-°6 = *6—7 -11, *2-6 - *2—6 - *2-6 =11-3 = 8.

Работа (3—5) предшествует всего одной работе — работе (5—7), значит, срок позднего окончания работы (3—5) — это срок позднего начала работы (5—7), следовательно:

Работы (2—4) и (1—4), имеющие общее конечное событие, пред­шествуют всего одной работе — работе (4—6), значит, срок позднего окончания работ (2—4) и (1—4) — это срок позднего начала рабо­ты (4—6). следовательно:

Работа (1—3) предшествуют двум работам — работам (3—5) и (3—7), значит, срок позднего окончания работы (1—3) определяется как минимум из поздних начал работ (3—5) и (3- 7), следовательно:

£,^,10з = min foⁿJj11₃-7> = min {8. 10} = 8, £,^п_^н₃ = £,^p_°₃ - £,_₃ = 8-2 = 6.

Работа (1—2) предшествует двум работам — работам (2—4) и (2—6), значит, срок позднего окончания работы (1—2) определяется как минимум из поздних начал работ (2—4) и (2—6), следовательно:

tfLS = min {£₂^ПД, *2-б} ⁼ min {5,8} = 5, tfL” = t™₂ ~ h-2 = 5-3 = 2.

Шаг 6. Определение полного и частного резервов всех работ.

2-<1^П-°2-«1^Р-⁰2-5-3 = 2 (/г, 2 = -«1-*2-2-0 = 2); г,-2 - t₂_J - - 3 - 3 - 0;

Ki-з = «1-°з - 'Гз = 8-2 = 6 (Я,_з = № - t}L^H₃ = 6-0-6);

г,_з = £₃^Р-” - fi-°3 = 2-2 = 0;

п _*ПО / РО _ г ГГ _ П. к — t PH fPO — С с - п.

/vj_4 — j —4 — 1.1_4 — О — О — U, /j_4 — £4-6 — f-i_4 — D — — U,

«2-4 = t2-°4 - t₂-°4 = 5-3 = 2; v2 ,₄ = tUb - t₂^p_°₄ = 5-3 = 2;

«2-6 = ^_ t2^P06 =11-6 = 5; r₂_₆ = =11-6 = 5;

R3 5 = tj’⁽l ~ t-П =12-6-6; r₃ 5 = t₅^p_^H₇ - £₃^p_°₅ = 6-6-0;

R3 7 = *з^П-° - <3-° =14-6-8; r_{3 7} = t$^p - tf°₇ =14-6-8;

tu ,i - t₄ⁿ-°6 - f«^p_°₆ - 14 - 8 - 6; r_{A 6} - C^H7 -1/-°6 - 11 - 11 - 0;

R5-7" f5ⁿ°7 -1₅-°7 - 14 - 8 - 6; r₅_₇ - - t₅^po₇ - 17 - 8 - 6;

«(i-7 ^{= f}e^n<7 ~ t(f*7 = 14 - 14 = 6; >(;_7 = £(j ^P - £|f⁽7 = 14 - 14 = 0.

Работы (1—4), (4—6) и (6—7), у которых величина полного резер­ва равна нулю, составляют критический путь в сети.

Сетевой график удобно представить в виде графика Гантта, где на оси ординат располагается перечень работ сети, а ось абсцисс представ­ляет собой шкалу времени (рис. 3.1). Каждая работа сети в координат­ной плоскости «работа—время» изображается в виде отрезка, длина которого отражает длительность выполнения этой работы. Координа­ты начала и конца отрезка по оси абсцисс — это ранние (поздние) вре­менные характеристики работы, т.е. сроки ее раннего (позднего) на­чала и раннего (позднего) окончания. График Гантта удобен тем, что вертикальное сечение в конкретной точке на оси времени позволяет быстро выявить соответствующий фронт выполняемых работ.

Время, ед.

Рис. 3.1. Линейное представление выполнения работ сети (график Гантта) по ранним временным характеристикам