1.5. Маршрути і підграфи

Визначення. Маршрут довжини m на графі – це послідовність m ребер графа (не обов'язково різних), таких, що граничні вершини двох сусідніх ребер співпадають. Маршрут проходить і через всі вершини, які інцидентні вхідним у нього ребрам.

Замкнутий маршрут – це маршрут, який приводить в ту ж вершину, з якої він почався. Маршрут, всі ребра якого різні, називається ланцюгом, а маршрут, для якого різні всі вершини, називається простим ланцюгом. Замкнутий ланцюг називається циклом, а простий замкнутий ланцюг – простим циклом.

Орієнтовані маршрути на орграфі визначаються аналогічно з тією різницею, що початкова вершина кожної подальшої дуги маршруту повинна співпадати з кінцевою вершиною попередньої дуги. Інакше кажучи, рух маршрутом допускається тільки в напрямах, вказаних стрілками.

Шлях – це маршрут, що не містить дуг, що повторюються. Простий шлях – це шлях, що не містить вершин, які повторюються (за виключенням, можливо, початку і кінця маршруту). Замкнутий шлях називається контуром, а простий замкнутий шлях – простим контуром. Граф (орграф) називається циклічним (контурним), якщо він містить хоч би один цикл (контур), інакше він називається ациклічним (безконтурним).

Приклад 6. Розглянемо граф, показаний на рис. 1.2, а. На цьому графі: (е₁, е₃, е₂, е₃, е₅) – маршрут, що проходить через послідовність вершин (v₁, v₂, v₃, v₂, v₃, v₅) і сполучає вершини v₁ і v₅; (е₅, е₆, е₄, е₄) – маршрут, що проходить через послідовність вершин (v₃, v₅, v₅, v₂, v₅), сполучаючи v₃ і v₅; (е₁, е₃, е₅, е₄, е₁) – замкнутий маршрут; (е₂, е₅, е₆) – ланцюг; (е₁, е₂, е₅) – простий ланцюг; (е₂, е₃, е₄, е₅) – цикл; (е₂, е₄, е₅) – простий цикл.

На орграфі рис. 1.4, а маршрут (е1, е2, е5) – простий шлях, що є контуром, а маршрут (е1, е2, е3) – простий неконтурний шлях.

Цикл, який містить всі ребра графа, називається ейлеровим циклом, а граф, у якому є такий цикл, називається ейлеровим графом. Простий цикл, який проходить через всі вершини графа, називають гамільтоновим. Якщо критерій існування ейлерового циклу дуже простий (необхідно, щоб степені всіх вершин були парними), то для гамільтонових циклів ніякого загального правила не знайдено.

Граф є частиною графа G = (V, V), якщо і , тобто граф містить всі вершини і ребра будь-якої його частини.

Визначення. Підграф – це частина графа, яка, разом з деякою підмножиною ребер графа, містить і всі інцидентні ним вершини. Суграф – це частина графа, яка разом з деякою підмножиною ребер графа містить всі вершини графа .

Початковий граф по відношенню до його підграфа називають надграфом, а по відношенню до суграфа – понадграфом. Сукупність всіх ребер графа, що не належать його підграфу (разом з інцидентними вершинами), утворює доповнення підграфа. Говорять, що підграфи одного графа і розділені ребрами, якщо вони не мають загальних ребер ( ) і розділені вершинами, якщо у них немає загальних вершин ( ).

П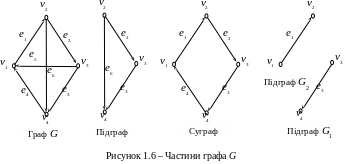 риклад 7. На рис. 1.6 показані різні частини кубічного орграфа G.

Різні частини кубічного орграфа G такі: підграфи , G₁ та G₂; суграф Підграфи G₁ та G₂ розділені ребрами і вершинами.