1.4. Способи задання графів
Геометричне подання – рисунок. Використовують з метою ілюстрації та як робочий документ (карти, схеми). Незручний з підвищенням кількості вершин.
Матриця суміжності графа (орграфа). Це квадратна матриця ij, елементи якої ij дорівнюють одиниці лише, якщо вершина і є інцидентна початку дуги, а вершина j інцидентна кінцю дуги, інакше елементи дорівнюють нулю. Неорієнтований граф має матрицю, яка симетрична відносно головної діагоналі. Спосіб має обмеження – неможливо задавати мультиграфи.
Матриця інцидентності. Це прямокутна матриця, в якій розмітка вздовж стовпця – ідентифікатори вершин графа, розмітка вздовж рядка – ідентифікатори дуг або ребер. Елемент матриці ij , тобто, ij , де і – номер рядка (а також вершини) і j – номер стовпця (а також дуги або ребра), набуває значень:
– якщо вершина і є початок дуги і, то ij = 1;
– якщо вершина і є кінець дуги і, то ij = –1;
– якщо вершина і не є інцидентна дузі або ребру і, то ij = 0.
У матриці інцидентності не більше двох елементів рядка є відмінні від нуля. Такий спосіб задання графів є універсальним, але не є економічним з точки зору використання пам'яті ЕОМ.
Список ребер (дуг). Тут у кожному рядку є відповідні номери дуги та вершин, що їй інцидентні. Це також універсальний, але набагато більш економічний спосіб з точки зору використання пам'яті ЕОМ.
Матриця досяжності орграфа. Це також квадратна матриця, де номери рядків та стовпців це номери вершин орграфа. Елементи матриці набувають значення одиниці лише тоді, коли існує шлях з вершини, що має номер рядка, у вершину, що має номер стовпця матриці. Цей спосіб задання не дозволяє розрізнити зв'язні графи. Для кожного орграфа можна задати матрицю досяжності. Але не всяка довільна матриця є матрицею досяжності орграфа, бо відшукати з її допомогою інші варіанти задання іноді неможливо (орграф не існує).
П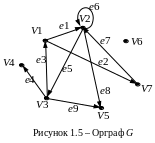
риклад
5.
Для орграфа G
(рис. 1.5) приготувати задання різними
способами.
e1
e2
e3
e4
e5
e6
e7
e8
e9
V1
1
1
-1
0
0
0
0
0
0
V2
-1
0
0
0
1
0
-1
1
0
V3
0
0
1
1
-1
0
0
0
1
V4
0
0
0
-1
0
0
0
0
0
V5
0
0
0
0
0
0
0
-1
-1
V6
0
0
0
0
0
0
0
0
0
V7
0
-1
0
0
0
0
1
0
0
V1
V2
V3
V4
V5
V6
V7
V1
0
1
0
0
0
0
1
V2
0
1
1
0
1
0
0
V3
1
0
0
1
1
0
0
V4
0
0
0
0
0
0
0
V5
0
0
0
0
0
0
0
V6
0
0
0
0
0
0
0
V7
0
1
0
0
0
0
0
Задання мультиграфа матрицею інцидентності не є проблемним, а ось ізольована вершина тут ніяк не позначена.
Кількість одиниць у матриці суміжності дорівнює кількості дуг орграфа.
3) Список дуг:
e1 |
e2 |
e3 |
e4 |
e5 |
e6 |
e7 |
e8 |
e9 |
V1 |
V1 |
V3 |
V3 |
V2 |
V2 |
V7 |
V2 |
V3 |
V2 |
V7 |
V1 |
V4 |
V3 |
V2 |
V2 |
V5 |
V5 |
4) Матриця досяжності орграфа G:
|
V1 |
V2 |
V3 |
V4 |
V5 |
V6 |
V7 |
V1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
V2 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
V3 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
V4 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
V5 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
V6 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
V7 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
Така матриця інформативна саме для орграфа, бо для зв'язного графа всі елементи матриці є одиницями, а для графа з декількома областями зв'язності у матриці буде декілька квадратних підматриць спільно з одиницями.