10.5. Виведення у кв-граматиках і правила побудови дерева виведення

Формальні граматики дозволяють задавати мови, що являють собою множину ланцюжків, побудованих за визначеними правилами. Використовуваний спосіб завдання дозволяє будь-як побудувати ланцюжок, що належить мові. Щоб зробити процес побудови, що називається наочним виведенням, його зображають у вигляді графа, точніше, у вигляді дерева, яке називають синтаксичним деревом, або деревом виведення. З огляду на те, що виведення будь-якого ланцюжка, який належить мові, породжуваній заданою граматикою, повинно починатися з початкового символу, правила побудови дерева можна сформулювати так:

1) як початок чи вершину кореня дерева візьмемо вершину, яку позначимо початковим символом граматики I; ця вершина утворить нульовий ярус дерева;

2) якщо при виведенні ланцюжка на черговому кроці використовується правило граматики A і вершина, позначена нетермінальним символом A, розташована на ярусі з номером k – 1, то до побудованого дерева потрібно додати стільки вершин, скільки міститься символів у ланцюжку ; треба розташувати ці вершини на ярусі k , позначити їх символами ланцюжка  і з'єднати ці вершини дугами з вершиною A.

Результатом виведення по дереву є множина кінцевих вузлів – листів, що виписуються при обході дерева ліворуч – униз і праворуч – нагору.

Розглянемо, наприклад, граматику Г_10.10.

Г_10.8: V_т = {a, b}, V_a = {I},

R = {I aIb (1)

I ab}, (2)

яка породжує мову L(Г₈) = {aa...abb...b}, де а і b повторюються по n разів (n = 1, 2, ...).

Виведення ланцюжка за допомогою правил цієї граматики має вигляд дерева, відображеного на рис. 10.1.

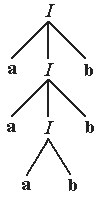
Рисунок 10.1 – Виведення ланцюжка aaabbb

10.5.1. Синтаксичний розбір. Виведення ланцюжка за допомогою правил граматики може бути задане не тільки у вигляді синтаксичного дерева. Якщо пронумерувати правила граматики, то послідовність номерів правил, які використані, також задає виведення.

Визначення. Послідовність номерів правил граматики Г, застосування яких дозволяє побудувати виведення заданого ланцюжка  з початкового символу граматики, називається синтаксичним розбором ланцюжка.

Наприклад, у граматиці Г_10.9

Г_10.9: V_т = {i, +, *, (, )}, V_a = {E, T, P}

R = {E  E + T (1)

E  T (2)

T  T * P (3)

T  P (4)

P  (E) (5)

P  i}, (6)

правила якої пронумеровані, виведення ланцюжка i * i + i буде таким:

E E + T T + T T * P + T P * P + T i * P + T i * i + T

i * i +P i * i + i.

Отже, послідовність використання правил є такою: 1, 2, 3, 4, 6, 6, 4, 6.

Якщо в процесі побудови виведення з'являються проміжні ланцюжки, що містять кілька нетермінальних символів, то можна продовжувати виведення, заміняючи кожний з ланцюжків. Таким чином, ті самі правила можуть бути використані при виведенні ланцюжка у будь-якому порядку.

Наприклад, виведення ланцюжка i + i в граматиці Г_10.9 може бути отримане декількома різними способами.

10.5.2. Ліве і праве виведення. Серед різних типів виведення найбільший інтерес становлять наступні два типи виведення.

Визначення. Якщо під час побудови виведення ланцюжка  при застосуванні кожного правила заміняється самий лівий нетермінальний символ, то таке виведення називається лівим, або лівостороннім виведенням . Але, якщо при побудові виведення  завжди заміняється самий правий нетермінальний символ проміжного ланцюжка, то таке виведення називається правим, або правостороннім виведенням .

Наприклад, наведене вище виведення ланцюжка i * i + i в граматиці Г_10.9 є лівостороннім виведенням. Слід зазначити, що різним виведенням ланцюжка i + i в граматиці Г_10.9 відповідає те ж саме синтаксичне дерево. Аналогічна ситуація має місце і при виведенні ланцюжка i * i + i.