9. Синтез мікропрограмного автомата за схемою алгоритму

9.1. Послідовність дій, необхідних для побудови управляючого пристрою

Найчастіше пристрої складаються з двох частин: виконавчої та управляючої. Виконавча частина пристрою зазвичай складна та незмінна. Управляюча частина значно простіша, може змінюватись, і вся гнучкість пристрою полягає саме в гнучкості управляючої частини. В обчислювальній машині одна із складних і незмінних частин – арифметичний пристрій. Однак на ньому можна виконати як додавання, так і обчислення синуса кута, або розв’язання диференціального рівняння, або щось інше. Що саме буде отримано, залежить від управляючої частини.

Взаємодія управляючої і виконуючої частин показана на рис. 9.1.

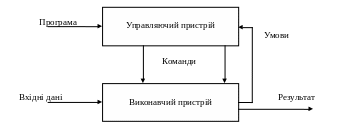
Рисунок 9.1 – Взаємодія управляючого і виконавчого пристроїв

Управляючий пристрій подає на виконавчий пристрій команди. Виконавчий пристрій виконує команди і, крім того, має набір булевих функцій, які виробляють «умови», що свідчать про ті або інші події у виконавчому пристрої. Основний потік вхідних даних надходить тільки у виконавчий пристрій. В управляючий пристрій надходить програма. Результати також надходять на вихід, минаючи управляючий пристрій. Програма завантажується в управляючий пристрій до початку обробки вхідних даних. Управляючий пристрій із завантаженою програмою є операційним автоматом, який настроєний на розв’язання завдання з обробки даних.

Зміст вироблення умов такий: програма повинна працювати з різними вхідними даними (тобто досить запустити її один раз). Хід обчислень може змінюватись залежно від вхідних даних. Розпізнавання ситуації, критичної для виконання програми, може бути складним завданням, тому воно виконується у виконавчому пристрої. Повідомлення про те, виникла критична ситуація чи ні, має тільки два значення: «так» або «ні». Повідомлення надходить в управляючий пристрій з виходу «Умови» виконавчого пристрою.

Таким чином, оскільки виконавчий пристрій не змінюється, то і функції, які виробляють умови, не змінюються. У роботі управляючого пристрою можуть використовуватися тільки такі умови, вироблення яких передбачене у виконавчому пристрої. Розглянемо випадок, коли потрібно виконувати ту саму програму для різних вхідних даних. Що являє собою управляючий пристрій? Як його можна реалізувати? Виявляється, відповідь можна дати мовою кінцевих автоматів. Управляючий пристрій – це кінцевий автомат. Вхідні сигнали для нього – умови і синхроімпульси, а вихідні – команди.

Створення управляючого автомата починається зі схеми алгоритму розв’язання завдання (рис. 9.2) Вона складається з таких блоків: «Початок», «Кінець», «Операційна вершина» (рис. 9.3), «Умовна вершина» (рис. 9.4).

Початок означає початок роботи алгоритму. Кінець – завершення його роботи. Операційна вершина означає роботу, яка виконується виконавчим пристроєм у фрагменті алгоритму. Вона має виконуватися однаково для всіх допустимих вхідних даних, тобто не містити розгалужень.

Умовна вершина містить булеву змінну, значення якої забезпечує вибір одного із двох напрямків подальшої роботи алгоритму.

Стрілки на лініях відображають порядок, в якому мають виконуватись блоки в схемі.

В міст операційних блоків може повторюватись так само, як і умови в умовних блоках.

При створенні автомата потрібно заздалегідь передбачити сукупність букв вхідного алфавіту для умовних блоків. Він має складатись із вхідних букв X_і, де х₀ – синхроімпульс. Остаточно вхідний алфавіт буде сформований у результаті розробки таблиці переходів.

Вихідний алфавіт – це команди, які формує управляючий автомат. Кожна команда запускає виконання деякого операційного блока або викликає перехід на умовний блок (без виконання операційного блока). «Порожню команду», що не запускає жодного блока, позначимо як y₀ (можна використовувати позначення у вигляді прочерку – «–»). Інші команди позначимо буквою Y_j з тим же номером, що і операційний блок, який ця команда запускає. В результаті отримаємо множину виходів.

Кількість внутрішніх станів S_k залежить від того, якого типу автомат створюється –Мілі чи Мура.

Побудова мікропрограмного автомата за схемою алгоритму (його іноді називають автоматом Уілкса-Стрінджера) зводиться до таких дій:

1) кодування операційних та умовних вершин;

2) побудова основної таблиці та граф-схеми переходів;

3) побудова системи рівнянь для функцій переходів і системи рівнянь для функцій виходів (останнє тільки для автоматів Мілі);

4) кодування внутрішніх станів автомата;

5) побудова функціональної схеми автомата.

Спочатку розглянемо послідовність дій, необхідних для побудови управляючого пристрою для автомата Мілі.