8.2. Синтез схем на мультиплексорах
Мультиплексором (МП) називається конструктивний елемент з одним виходом і двома групами входів, а саме адресними входами (входи управління, інакше селекторні входи) і входами даних. МП дозволяє подачею певних двійкових векторів на адресні входи підключати до виходу потрібні вхідні дані. Фактично МП являється комутатором, який відповідний вхід даних підключає до свого виходу. Необхідний вхід даних вибирається за допомогою відповідного значення на адресних входах. Нині під час проектування засобів обчислювальної техніки широко використовуються мультиплексори, які фізично реалізовані в одному корпусі інтегральної мікросхеми середнього ступеня інтеграції.
Позначимо
буквами xi
{0, 1} адресні
входи МП, а буквами аi
{0, 1} – інформаційні входи. Якщо МП має
n адресних
входів, то інформаційних входів (тобто
входів даних) – 2n.
В табл. 8.4 подана таблиця істинності мультиплексора з двома адресними входами x1 і x2 і чотирма інформаційними входами a0, a1, a2, і a3.
Таблиця 8.4 – Таблиця істинності мультиплексора
Значення адресних входів |
Значення виходу f |
|
x1 |
x2 |
|
0 |
0 |
a0 |
0 |
1 |
a1 |
1 |
0 |
a2 |
1 |
1 |
a3 |
Якщо на адресні входи мультиплексора подати 00, то до виходу підключиться вхідний сигнал а0. В залежності від значення а0 на виході з’явиться нульовий або одиничний сигнал.
Умовне зображення МП з двома адресними і чотирма інформаційними входами подане на рис. 8.5.
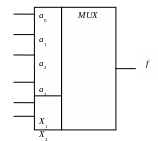
Рисунок 8.5 – Умовне зображення МП з двома адресними і чотирма інформаційними входами
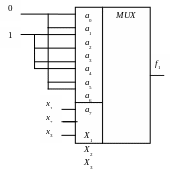
Якщо на входи даних a0, a1, …, a2^k-1 подати двійковий вектор, який відповідає стовпцю значень заданої функції f в таблиці істинності, а на адресні входи – значення змінних, наведених в таблиці істинності, то МП реалізує функцію f (x1, x2, …, xk). Відмітимо, що в описаному способі реалізації функції f на входи даних МП подаються константи (константа 0 і константа 1) у відповідності зі значеннями функції в її таблиці істинності. Приклад реалізації функції f1 (x1, х2, x3) (табл. 8.5) наведений на рис. 8.6.
В ряді випадків МП має додатковий вхід xR, який називається cтробом. Функціональне призначення строба таке: якщо хR = 1, то на виході МП буде нульове значення (незалежно від двійкового набору, поданого на адресні входи); якщо xR = 0, то МП функціонуватиме як завжди.
Найчастіше використовуються МП, реалізовані у вигляді однієї інтегральної мікросхеми.
Таблиця 8.5 – Таблиця істинності функції f1 (x1, х2, x3)
|
Рисунок 8.6 – Реалізація функції f1 (x1, х2, x3) на мультиплексорі
|
Якщо
МП має n
адресних
входів, то на такому МП можна реалізувати
будь-яку булеву функцію (п
+ 1) змінних. Дійсно, задамо функцію f
(x1,
x2,
..., xn+1)
її таблицею істинності. Змінні x1,
x2,
..., xn
виділимо як адресні змінні МП, а змінну
xn+1
– як змінну
даних МП. Тоді можливі такі чотири
ситуації для будь-яких двох сусідніх
двійкових наборів довжини (n
+ 1) з однаковою адресною частиною: 1) f
= 1; 2) f
= 0; 3) f
= xn+1;
4) f
=
n+1.
Таким чином, якщо змінні x1,
x2,
..., xn
подати на адресні входи МП, то для
реалізації функції f
(х1,
х2,
…, xn+1)
необхідно на кожному вході даних МП
реалізувати або константу 0, або константу
1, або xn+1,
або
n+1
(що визначається таблицею істинності
функції).
Приклад
3.
Реалізуємо
на МП з трьома адресними входами булеву
функцію f2
(x1,
x2,
x3,
x4)
(табл. 8.6). Виділимо змінні x1,
x2
і x3
як адресні змінні МП. Тоді: якщо на
адресні входи МП (табл. 8.6) поступає набір
000, то f2
= х4;
якщо поступають набори 001, або 010, або
100, то f2
=
;
якщо поступають набори 011, або 101, то f2
= 1 і, нарешті, якщо поступають набори
110, або 111, то f2
= 0. Таким чином, отримуємо реалізацію
булевої функції, подану на рис. 8.7.
Константа 0 реалізується підключенням
відповідного входу даних МП до “землі”,
а константа 1 – підключенням відповідного
входу даних МП до шини живлення.
Таблиця 8.6 – Таблиця істинності функції f2 (x1, x2, x3, x4)
Входи MUX |
x1 |
x2 |
x 3 |
x 4 |
f2 |
Значення на входах MUX |
0 |
0 |
0 |
0 |
0 |
0 |
х4 |
0 |
0 |
0 |
1 |
1 |
||
1 |
0 |
0 |
1 |
0 |
1 |
|
0 |
0 |
1 |
1 |
0 |
||
2 |
0 |
1 |
0 |
0 |
1 |
|
0 |
1 |
0 |
1 |
0 |
||
3 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
||
4 |
1 |
0 |
0 |
0 |
1 |
|
1 |
0 |
0 |
1 |
0 |
||
5 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
||
6 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
||
7 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
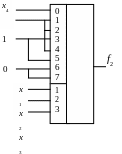
Рисунок 8.7 – Реалізація булевої функції f2 (x1, x2, x3, x4)
Контрольні запитання
Призначення та особливості функціонування дешифраторів і мультиплексорів.
Як за допомогою дешифратора реалізувати функцію, задану її таблицею істинності, наприклад?
Як функціонує схема, наведена на рис. 8.4?
Які групи входів існують у мультиплексора?
Як на мультиплексорі реалізувати функцію, яка залежить від більшої кількості змінних, ніж кількість адресних входів у мультиплексора?