7.7. Побудова функціональної схеми автомата
Функціональна схема автомата наведена на рис. 7.7.
Введемо
цифрові позначення: 1 – прямий вхідний
сигнал Аt;
2 – інверсний вхідний сигнал
;
3 – прямий вихід тригера Т1;
4 – інверсний вихід тригера Т1;
5 – прямий вихід тригера Т2;
6 – інверсний вихід тригера Т2;
7 – вихідний сигнал Сt.
Згідно з рівнянням (7.1) на вхід тригера
Т1 має
подаватись сигнал з виходу схеми АБО-НІ,
на вхід якої треба подати вхідний сигнал
Аt
і інверсний
вихідний сигнал другого тригера Т2.
1
6
51
1
2
4
2
5
1
1
1
1
1
1
1
1
Т2
Т
4
2
7
Т1
Т
7
3
5
1
1
1
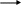
41
5
Рисунок 7.5 – Функціональна схема автомата
Аналогічно треба побудувати іншу частину схеми у відповідності до рівнянь (7.2) і (7.3).
Контрольні запитання
Назвіть два класи елементарних автоматів.
Які етапи канонічного методу структурного синтезу автомата ви знаєте?
Як будується основна таблиця абстрактного автомата?
Як кодуються вхідні, внутрішні і вихідні стани автомата?
Як будується закодована таблиця структурного автомата?
Як будується канонічна таблиця структурного автомата?
Які тригери використовуються в якості елементів пам’яті структурного автомата?
Які особливості побудови таблиць переходів для різних тригерів?
Як будується таблиця збудження тригера?
Як складаються системи рівнянь функцій збудження тригера і виходів автомата?
Як описуються правильні конфігурації карт Карно?
Як побудувати функціональну схему автомата?
8. Проектування комбінаційних схем на дешифраторах і мультиплексорах
8.1. Синтез схем на дешифраторах
Дешифратором називається комбінаційна схема, яка реалізує всі конституенти одиниці. Іншими словами, дешифратор – це схема, що має п входів і 2n виходів. Вона включає один із вихідних каналів, тобто тільки на одному з виходів з’являється одиничне значення, при подачі відповідного двійкового набору на n входів. Дешифратор являється типовою комбінаційною схемою, яка знаходить широке застосування в обчислювальній техніці. Тому дешифратори на невелику кількість змінних, а саме, коли п не більше чотирьох, виготовляються у вигляді стандартних мікросхем. Однак, в ряді випадків на практиці приходиться будувати дешифратори з десятками тисяч виходів, наприклад, в запам’ятовуючих пристроях і електронних комутаторах. Дешифратор, який має три входи, задається таблицею істинності, що наведена в табл. 8.1.
Таблиця 8.1 – Таблиця істинності дешифратора на три входи
x1 |
x2 |
x3 |
D0 |
D1 |
D2 |
D3 |
D4 |
D5 |
D6 |
D7 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
Із визначення конституенти одиниці очевидно, що під час синтезу дешифраторів доцільно використовувати тільки елементи типу І або АБО-НІ. Умовне позначення дешифратора на три входи подане на рис. 8.1
Рисунок 8.1 – Дешифратор на три входи
За допомогою дешифратора легко реалізувати довільну булеву функцію, об’єднавши за допомогою схеми АБО ті його виходи, які відповідають одиницям в таблиці істинності булевої функції. Об’єднувати можна і виходи, які відповідають нулям в таблиці істинності булевої функції. Але для об’єднання необхідно використати схему АБО-НІ.
Приклад 1. Реалізувати за допомогою дешифратора суматор за модулем два («Виключне АБО»).
Таблиця істинності суматора за модулем два має такий вигляд (табл. 8.2):
Таблиця 8.2 – Таблиця істинності суматора за модулем два
х1 |
х2 |
y |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
Нам знадобиться дешифратор на два входи. Якщо ми об’єднаємо за допомогою схеми АБО ті його виходи, які відповідають одиницям в табл. 8.2 (набори 01 і 10), то отримаємо рівняння (8.1).
(8.1)
Реалізація суматора за модулем два за допомогою дешифратора наведена на рис. 8.2.
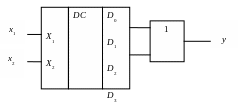
Рисунок 8.2 – Реалізація суматора за модулем два за допомогою дешифратора
Приклад 2. Реалізувати за допомогою дешифратора пристрій візуальної індикації десяткових цифр на світловому табло.
Позначимо змінними а1, а2, …, а7 лінії індикації, за допомогою яких можна отримати зображення десяткових цифр від 0 до 9 (рис. 8.3). Так, для отримання зображення цифри нуль мають бути обраними усі лінії, окрім лінії а7. Для отримання зображення одиниці мають бути обраними лінії а2 і а3. Подібні міркування для отримання зображення всіх десяткових цифр відобразимо у вигляді табл. 8.3.
а1
-
а6
а7
а2
а5
а3
а4
Рисунок 8.3 – Розміщення ліній візуальної індикації для отримання зображення десяткових цифр на світловому табло
Таблиця 8.3 – Таблиця отримання візуального відображення десяткових цифр
Десяткова цифра |
Двійковий код |
Значення ліній індикації |
|||||||||
x1 |
x2 |
x3 |
x4 |
a1 |
а2 |
а3 |
а4 |
a5 |
а6 |
а7 |
|
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
2 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
3 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
4 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
5 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
6 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
7 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
8 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
9 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
Нам знадобиться дешифратор на чотири входи. В табл. 8.3 маємо сім вихідних функцій а1, а2, …, а7, які відповідають вибору тієї чи іншої лінії індикації. Необхідно спочатку скласти рівняння для кожної з цих функцій. Так, якщо об’єднати за допомогою схеми АБО-НІ виходи дешифратора D1 і D4, які відповідають нулям в таблиці істинності для вихідної функції а1 (набори 0001 і 0100), то отримаємо реалізацію для функції а1:
(8.2)
Об’єднавши за допомогою схеми АБО-НІ виходи дешифратора D5 і D6, отримаємо реалізацію для функції а2:
(8.3)
Аналогічно отримаємо наступні рівняння:
а3 = D2 (8.4)
(8.5)
(8.6)
(8.7)
Функцію а5 простіше реалізувати, об’єднавши за допомогою схеми АБО ті виходи дешифратора, на яких ця функція приймає одиничні значення:
(8.8)
Реалізація пристрою візуальної індикації десяткових цифр на світловому табло за допомогою дешифратора подана на рис. 8.4.
Рисунок 8.4 – Схема пристрою візуальної індикації десяткових цифр на
світловому табло