1.3. Суміжність та інцидентність

Визначення. Дві вершини v_i і v_j  V графа G = (V, E) називаються суміжними, якщо вони є граничними вершинами ребра е_k  E.

Відношення суміжності на множині вершин графа можна визначити, представивши кожне ребро як пару суміжних вершин, тобто e_k = (v_i, v_j), k = 1, 2, … q. Для неорієнтованих графів такі пари невпорядковані, тобто е_k = (v_i, v_j) = = (v_j, v_i), а для орграфів – впорядковані, причому v_i і v_j означають відповідно початкову і кінцеву вершини дуги е_k. Петля при вершині v_i представляється парою (v_i, v_i). Множина вершин V разом з визначеним на ній відношенням суміжності повністю описує граф.

Граф можна представити матрицею суміжності. Рядки і стовпці цієї квадратної матриці відповідають вершинам графа, а її (ij)-елемент дорівнює числу кратних ребер, що сполучають вершини v_i і v_j (або направлені від вершини v_i до вершини v_j для орграфа).

Матриця суміжності неорієнтованого графа завжди симетрична, а орграфа – несиметрична. Неорієнтованим ребрам відповідають пари ненульових елементів, симетричних відносно головної діагоналі матриці, дугам – ненульові елементи матриці, а петлям – ненульові елементи головної діагоналі. У стовпцях і рядках, відповідних ізольованим вершинам, всі елементи дорівнюють нулю. Елементи матриці простого графа завжди дорівнюють 0 або 1, причому всі елементи головної діагоналі нульові.

Приклад 2. Графи, наведені на рис. 1.2, а і 1.3, описуються матрицями суміжності V₁ і V₂:

	v1	v2	v3	v4	v5				v1	v2	v3	v4
		1				v1				1			v1
	1		2		1	v2					1	1	v2
V1 =		2			1	v3		V2 =	1			1	v3
						v4			1				v4
		1	1		1	v5

Для зваженого графа, що не містить кратних ребер, можна узагальнити матрицю суміжності так, що кожен її ненульовий елемент дорівнює вазі відповідного ребра або дуги. Будь-яка квадратна матриця n-го порядку може бути представлена орграфом з n вершинами, дуги якого сполучають суміжні вершини і мають ваги, рівні відповідним елементам матриці. Якщо матриця симетрична, то вона може бути представлена неорієнтованим графом.

Визначення. Якщо вершина v_i є кінцем ребра e_k,, то говорять, що вони інцидентні: вершина v_i інцидентна ребру e_k і ребро e_k інцидентне вершині v_i.

Тоді як суміжністю є відношення між однорідними об'єктами (вершинами), інцидентність – це відношення між різнорідними об'єктами (вершинами і ребрами). При розгляді орграфів розрізняють додатну інцидентність (дуга виходить з вершини) і від'ємну інцидентність (дуга заходить у вершину).

Для (р,q)-графа можна побудувати матрицю інцидентності розміру р  q, рядки якої відповідають вершинам, а стовпці – ребрам. Для неорієнтованого графа елементи цієї матриці визначаються за таким правилом: ij-елемент дорівнює 1, якщо вершина v_i інцидентна ребру e_j, і дорівнює нулю, якщо v_i, і e_j не інцидентні. У випадку орграфа ненульовий ij-елемент дорівнює 1, якщо v_i початкова вершина дуги e_j, і дорівнює –1, якщо v_i – кінцева вершина дуги e_j.

Приклад 3. Матриці інцидентності графів, наведених на рис. 1.2, a і 1.3, мають відповідно такий вигляд:

	e1	e2	e3	e4	e5	e6					e1	e2	e3	e4	e5	e6
	1						v1				1			-1	-1		v1
A1 =	1	1	1	1			v2	;		A2 =	-1	1				1	v2
		1	1		1		v3					-1	1		1		v3
							v4						-1	1		-1	v4
				1	1		v5

Кожен стовпець матриці інцидентності обов'язково містить два одиничні елементи (для орграфа ці елементи завжди мають різні знаки і дорівнюють відповідно 1 і –1). Кількість одиниць в рядку рівна степеню відповідної вершини (для орграфа кількість додатних одиниць визначає додатний степінь, а кількість від'ємних одиниць – від'ємний степінь). Нульовий рядок відповідає ізольованій вершині, а нульовий стовпець – петлі, причому нульовий стовпець матриці інцидентності лише вказує на наявність петлі, але не містить відомостей про те, з якою вершиною ця петля пов'язана (тобто матриця інцидентності неоднозначно визначає граф, проте в практичному застосуванні це може бути несуттєво).

Визначення. Графи, для яких зберігається відношення інцидентності, називаються ізоморфними.

Приклад 4. Графи, зображені на рис. 1.4, мають таку ж матрицю інцидентності (А₂), як і граф рис. 1.3, проте з геометричної точки зору вони абсолютно різні, хоча розрізняються лише зображенням, а відношення інцидентності (при відповідному позначенні вершин і ребер) однакові.

З

а б

Рисунок 1.4 – Ізоморфні графи

розуміло, що матриця інцидентності визначає граф без петель з точністю до ізоморфізму. Зазвичай на її основі можна зобразити різні в геометричному відношенні, але ізоморфні між собою графи, кожен з яких називають геометричною реалізацією.

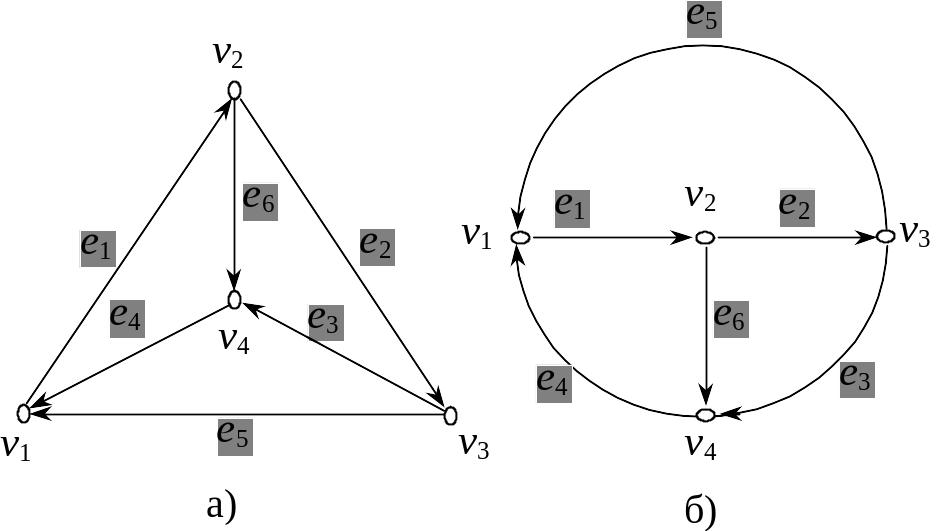
Якщо істотні властивості графа не пов'язані зі способом його зображення на площині або нумерацією вершин і ребер, то ізоморфні графи, як правило, не розрізняються між собою.