5.5. Мінімальна Пірсівська нормальна форма

Операція стрілка Пірса або операція АБО-НІ являється функціонально-повним базисом. Тому за допомогою операції стрілка Пірса може бути подана будь-яка булева функція.

Для отримання мінімальної Пірсівської нормальної форми (МПНФ) необхідно виконати такі дії:

• заносимо нульові значення функції в карту Карно;

• створюємо ПК за нульовими значеннями. Нулі, які ввійшли на попередніх кроках в одну із ПК, вважаємо покритими. Із непокритих і покритих нулів створюємо наступну ПК, стараючись при цьому покрити максимальну кількість непокритих нулів. Нову ПК тільки із покритих нулів створювати не треба. Процес завершується, коли покриті всі нулі;

• описуємо всі ПК за допомогою таблиці;

• змінні, від яких залежить ПК, об’єднуємо за допомогою операції стрілка Пірса. Якщо змінна для даної ПК приймає одиничне значення, то вона береться в інверсному вигляді, інакше – в прямому:

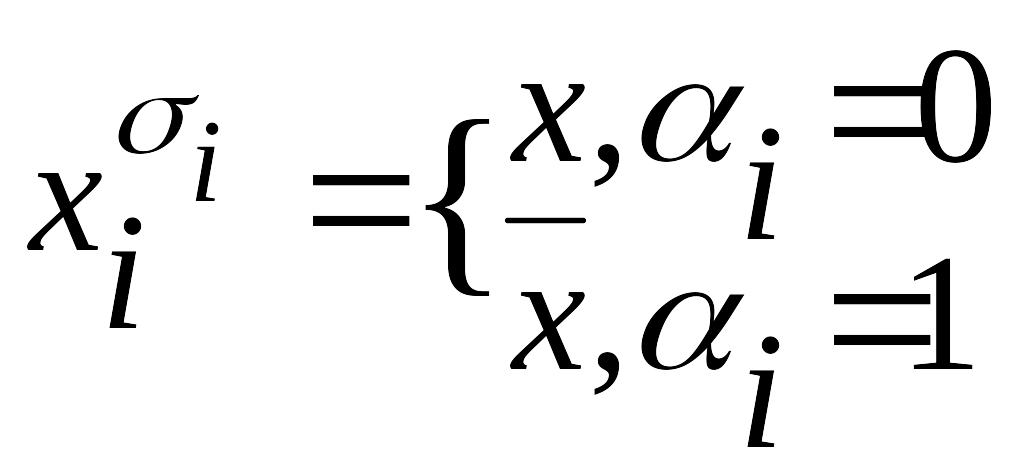
Виняткові ситуації:

• якщо ПК має максимальний ранг (тобто описується тільки однією змінною), то змінна, яка описує ПК, береться в інверсному вигляді;

• якщо має місце тільки одна ПК, то береться загальна інверсія над усіма змінними, які описують цю ПК.

Об’єднуємо за допомогою операції стрілка Пірса всі описані ПК:

й отримуємо мінімальну Пірсівську нормальну форму.

Приклад 6. Функція f₆ задана таблицею істинності (табл. 5.12). Побудувати МПНФ.

Таблиця 5.12 – Таблиця істинності функції f₆

x1	х2	х3	f6
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	0
1	0	0	1
1	0	1	1
1	1	0	1
1	1	1	1

Заносимо нульові значення функції f₆ в карту Карно.

х₁ ПК₁²

х2	6	7	0 3	0 2
	4	5	0 1	0 0

х₃

Об’єднуємо клітинки 0, 1, 2 і 3 в ПК₁². Правильна конфігурація ПК₁² описується за допомогою табл. 5.15.

Таблиця 5.13 – Опис значень змінних для правильної конфігурації за нульовими значеннями функції f₆

Правильна Конфігурація	Значення змінних
	х1	х2	х3
ПК12	0	–	–

В даному випадку мають місце одночасно дві виняткові ситуації. Тому

f_{6 мпнф} = = .

Контрольні запитання

1. Які мінімальні нормальні форми булевих функцій ви можете назвати?

2. Які особливості використання карт Карно для отримання мінімальних нормальних форм булевих функцій?

3. Що являють собою правильні конфігурації (ПК)?

4. Як отримуються порядкові набори клітин карти Карно?

5. Які клітини карти Карно є сусідніми?

6. Що таке ранг правильної конфігурації?

7. Як обчислюється кількість змінних які описують ПК.

8. Як описуються правильні конфігурації?

9. Які дії треба виконати, щоб отримати такі мінімальні нормальні форми булевих функцій: диз’юнктивну, кон’юнктивну, Шефферівську і Пірсівську?

10. Побудувати МДНФ, МКНФ, МПНФ, МШНФ для наступної функції:

f₅ (x₁, x₂, x₃, х₄) = ( 1, 2, 3, 4, 7, 8, 12, 13, 14, 15)¹.